Trong không gian Oxyz, cho mặt phẳng (P) có phương trình là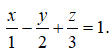 

Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P):

I. Vecto pháp tuyến của mặt phẳng.

1.  Định nghĩa:

Cho mặt phẳng (α). Nếu vecto $\overrightarrow{n}\ne \overrightarrow{0}$ và có giá vuông góc với mặt phẳng (α) thì $\overrightarrow{n}$ được gọi là vecto pháp tuyến của (α)

2. Chú ý. Nếu là $\overrightarrow{n}$ vecto pháp tuyến của một mặt phẳng thì $k\overrightarrow{n}(k\ne 0)$ cũng là vecto pháp tuyến của  mặt phẳng đó. 

3. Tích có hướng của hai vectơ

- Định nghĩa: Trong không gian Oxyz, cho hai vectơ $\overrightarrow{a}=(a_1;a_2;a_3)$. Tích có hướng của hai vectơ $\overrightarrow{a}$ và  $(\overrightarrow{b}$ kí hiệu là $[\overrightarrow{a},\overrightarrow{b}]$, được xác định bởi

$[\overrightarrow{a},\overrightarrow{b}]=(\left|\begin{array}{c}{a}_2 a_3\\ b_2 b_3\end{array}\right|;\left|\begin{array}{cc}{a}_3& a_1\\ b_3& b_1\end{array}\right|;\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|)=(a_2{b}_3-a_3{b}_2;a_3{b}_1-a_1{b}_3;a_1{b}_2-a_2{b}_1)$

- Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

Ví dụ 1. Trong không gian Oxyz, cho ba điểm A(2; 1;1); B(-1; 2; 0) và C(0; 1; -2).

Hãy tìm tọa độ của một vecto pháp tuyến của mặt phẳng (ABC).

Lời giải:

Ta có: $\overrightarrow{AB}(-3;1;-1);\overrightarrow{AC}(-2;\mathrm{\hspace{0.17em}0};-3)$

Một vecto pháp tuyến của mặt phẳng (ABC) là :

$\overrightarrow{n}=[\overrightarrow{AB};\overrightarrow{AC}]=(-3;-7;2)$.

II. Phương trình tổng quát của mặt phẳng

1. Định nghĩa.

- Phương trình có dạng Ax + By + Cz + D = 0 trong đó A; B; C không đồng thời bằng 0 , được gọi là phương trình tổng quát của mặt phẳng.

- Nhận xét.

a) Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một vecto pháp tuyến là $\overrightarrow{n}(A;B;C)$.

b) Phương trình mặt phẳng đi qua điểm M (x₀; y₀; z₀) và nhận vectơ $\overrightarrow{n}(A;B;C)$  khác $\overrightarrow{0}$ là vecto pháp tuyến là: A(x- x₀ ) + B( y – y₀) + C(z – z₀) = 0.

Ví dụ 1. Mặt phẳng 2x – y + 3z – 10 = 0 có một vecto pháp tuyến là $\overrightarrow{n}(2;-1;3)$.

Ví dụ 2. Lập phương trình tổng quát của mặt phẳng (ABC) với A(0; 1; -2); B(2; 1; 0); C ( -2; 1; 1)

Lời giải:

Ta có: $\overrightarrow{AB}(\mathrm{\hspace{0.17em}2};0;2);\overrightarrow{BC}(-4;0;1)$

Một vecto pháp tuyến của mặt phẳng (ABC) là $\overrightarrow{n}=[\overrightarrow{AB};BC]=(0;-10;0)$

Phương trình tổng quát của mặt phẳng (ABC) là:

0(x – 0) – 10(y – 1) + 0(z + 2) = 0 hay  y – 1 = 0.

2. Các trường hợp riêng

Trong không gian Oxyz, cho mặt phẳng (α) :  Ax + By + Cz + D =  0.

a) Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.

b)

- Nếu $A=0,B\ne 0,C\ne 0$ thì mặt phẳng (α) song song hoặc chứa trục Ox.

- Nếu $A\ne 0,B=0,C\ne 0$ thì mặt phẳng (α) song song hoặc chứa trục Oy.

- Nếu $A\ne 0,B\ne 0,C=0$ thì mặt phẳng (α) song song hoặc chứa trục Oz.

c)

- Nếu  A = B = 0; $C\ne 0$ thì mặt phẳng (α) song song hoặc trùng với (Oxy).

- Nếu A = C = 0; $B\ne 0$ thì mặt phẳng (α) song song hoặc trùng với (Oxz).

- Nếu B = C = 0; $A\ne 0$ thì mặt phẳng (α) song song hoặc trùng với (Oyz).

- Nhận xét:

Phương trình mặt phẳng theo đoạn chắn $(\alpha \mathrm{ }):\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$. Ở đây (α) cắt các trục tọa độ tại các điểm (a; 0; 0); (0; b; 0); (0; 0; c) với $abc\ne 0$.

Ví dụ 3. Trong không gian Oxyz, cho ba điểm M(2; 0; 0); N(0; 3; 0); P(0; 0; 1). Phương trình đoạn chắn của mp(MNP) là:

$\frac{x}{2}+\frac{y}{3}+\frac{z}{1}=1$

III. Điều kiện để hai mặt phẳng song song, vuông góc.

Trong không gian Oxyz, cho hai mặt phẳng (α) và (β) có phương trình:

(α): A₁x + B₁y + C₁z + D₁ = 0

(β): A₂x + B₂y + C₂z + D₂ = 0

Hai mặt phẳng (α); (β) có hai vecto pháp tuyến lần lượt là:

$\overrightarrow{n_1}(A{}_1;B_1;C_1);\overrightarrow{n_2}(A{}_2;B_2;C_2)$

1. Điều kiện để hai mặt phẳng song song.

$\begin{array}{c}\left(\alpha \right)//\left(\beta \right)\iff \{\begin{array}{c}\overrightarrow{n_1}=k.\overrightarrow{n_2}\\ D_1\ne k{D}_2\end{array}\iff \{\begin{array}{c}(A_1;B_1;C_1)=k(A_2;B_2;C_2)\\ D_1\ne k{D}_2\end{array}\end{array}$

$\begin{array}{c}\left(\alpha \right)\equiv \left(\beta \right)\iff \{\begin{array}{c}\overrightarrow{n_1}=k.\overrightarrow{n_2}\\ D_1=k{D}_2\end{array}\iff \{\begin{array}{c}(A_1;B_1;C_1)=k(A_2;B_2;C_2)\\ D_1=k{D}_2\end{array}\end{array}$

- Chú ý:  Để (α) cắt (β) $\iff \overrightarrow{n_1}\ne k.\overrightarrow{n_2}\mathrm{ }\iff (A_1;B_1;C_1)\ne k(A_2;B_2;C_2)$.

Ví dụ 4. Viết phương trình mặt phẳng (α) đi qua A(2; 1; 2) và song song với mặt phẳng (P): x – y + 2z – 1 = 0.

Lời giải:

Vì mp(α) song song với mặt phẳng (P): x – y + 2z – 1 = 0 nên $\overrightarrow{n_{\alpha }}=(1;-1;2)$

Mặt phẳng (α) đi qua A(2;1; 2) nên có phương trình:

1( x – 2) – 1(y – 1) + 2( z – 2) = 0 hay x – y + 2z – 5 = 0.

2. Điều kiện để hai mặt phẳng vuông góc.

$\begin{array}{c}\left(\alpha \right)\perp \left(\beta \right)\iff \overrightarrow{n_1}\perp \overrightarrow{n_2}\iff A_1{A}_2+B_1{B}_2+C_1{C}_2=0\end{array}$

Ví dụ 5. Viết phương trình mặt phẳng (P) đi qua A(1; 0; 1); B( 2; 1; -1) và vuông góc với mặt phẳng (Q): x – y + 2z – 1 = 0

Lời giải:

Ta có vecto pháp tuyến của mặt phẳng (Q) là: $\overrightarrow{n_Q}=(1;-1;2)$

Và $\overrightarrow{AB}(1;1;-2)$

Vì $\overrightarrow{n_P}\perp \overrightarrow{n_Q};\overrightarrow{n_P}\perp \overrightarrow{AB}$ nên $\overrightarrow{n_P}=[\overrightarrow{n_Q};\overrightarrow{AB}]=(0;4;2)$

Phương trình mặt phẳng (P) là:

0(x – 1) + 4(y – 0) + 2(z – 1) = 0 hay 4y – 2z – 2 = 0

IV. Khoảng cách từ một điểm đến một mặt phẳng.

- Định lí: Trong không gian Oxyz, cho điểm M₀(x₀; y₀; z₀) và mặt phẳng (α): Ax + By + Cz + D = 0 .

Khi đó khoảng cách từ điểm M₀ đến mặt phẳng (α) được tính:

$d(M_0,\left(\alpha \right))=\frac{|A{x}_0+B{y}_0+C{z}_0+D|}{\sqrt{A^2+B^2+C^2}}$.

Ví dụ 6. Tính khoảng cách từ điểm M(2; 3; 0) và N( 1; 1; 1) đến mặt phẳng (P): 2x – y + 2z + 1 = 0.

Lời giải:

Theo công thức tính khoảng cách từ một điểm đến mặt phẳng ta có:

$d(M;\left(P\right))=\frac{|2.2-3+2.0+1|}{\sqrt{2^2+{(-1)}^2+{\mathrm{\hspace{0.17em}2}}^2}}=\frac{2}{3}$

$d(N;\left(P\right))=\frac{|2.1-1+2.1+1|}{\sqrt{2^2+{(-1)}^2+{\mathrm{\hspace{0.17em}2}}^2}}=\frac{4}{3}$

Ví dụ 7. Tính khoảng cách giữa hai mặt phẳng song song được cho bởi phương trình: (P): x – 2y +2z + 3 = 0 và (Q): x – 2y + 2z – 7= 0.

Lời giải:

Ta biết khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.

Lấy điểm A(-3; 0; 0) thuộc mặt phẳng (P).

Ta có: $d(\left(P\right);\left(Q\right))=d(A;\left(Q\right))=\frac{|-3-2.0+2.0-7|}{\sqrt{1^2+{(-2)}^2+{\mathrm{\hspace{0.17em}2}}^2}}=\frac{10}{3}$.