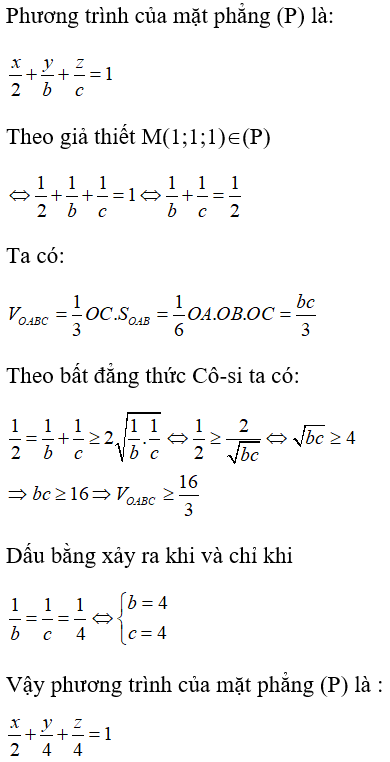66 câu trắc nghiệm: Phương trình mặt phẳng có đáp án (P1)
-
2285 lượt thi
-
31 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong không gian Oxyz, cho hai điểm A(1;0;-2), B(-1;1;1). Phương trình mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:
 Xem đáp án
Xem đáp án
Đáp án A
Do (P) ⊥ AB nên mp(P) có một vectơ pháp tuyến là = (-2; 1; 3). Mặt khác (P) đi qua điểm A nên phương trình của mặt phẳng (P) là:
-2(x - 1) + (y - 0) + 3(z + 2) = 0 ⇔ -2x + y + 3z + 8 = 0 ⇔ 2x - y - 3z - 8 = 0.
Vậy đáp án đúng là A.
Câu 2:
Trong không gian Oxyz, cho hai điểm A(1;3;5), B(-1;5;3). Lập phương trình mặt phẳng trung trực (P) của đoạn thẳng AB
 Xem đáp án
Xem đáp án
Đáp án C
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB. Ta có
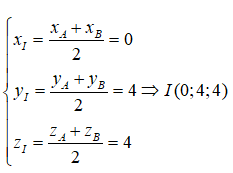
Ta chọn:
![]()
Vậy phương trình của mặt phẳng (P) là:
-2(x - 0) + 2(y - 4) - 2(z - 4) = 0 ⇔ -2x + 2y - 2z = 0 ⇔ x - y + z = 0
Vậy đáp án đúng là C.
Câu 3:
Trong không gian Oxyz, gọi lần lượt là hình chiếu vuông góc của điểm A(4;3;2) trên các trục Ox, Oy, Oz. Trong các khẳng định sau, khẳng định nào sai?
 Xem đáp án
Xem đáp án
Đáp án D
Vì lần lượt là hình chiếu vuông góc của điểm A(4;3;2) lên các trục Ox, Oy, Oz nên ta có (4; 0; 0), (0; 3; 0), (0; 0; 2).
Từ đó suy ra các khẳng định A và B là đúng.
Thể tích của khối tứ diện
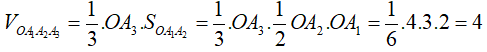
Nên khẳng định C là đúng.
Vậy khẳng định D sai.
Câu 4:
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;1 ;-3), vuông góc với mặt phẳng (Q): x + y - 3z = 0 đồng thời (P) song song với trục Oz.
 Xem đáp án
Xem đáp án
Đáp án B
Mặt khác (P) đi qua điểm A(2 ;1 ;-3) nên ta có phương trình của mặt phẳng (P) là:
1(x - 2) - 1(y - 1) + 0(z + 3) = 0 x - y - 1 = 0.
Vậy đáp án đúng là B
Câu 5:
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1 ;0 ;1), B(0 ;-1 ;-3), C(3 ;2 ;5).
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta suy ra
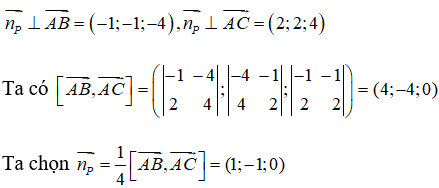
Mặt khác (P) đi qua điểm A(1 ;0 ;1) nên ta có phương trình của mặt phẳng (P) là :
1(x - 1) - 1(y - 0) + 0(z - 1) = 0 x - y - 1 = 0.
Vậy đáp án đúng là A.
Câu 6:
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;2) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án D
Ta có OA ⊥ OB, OC OA ⊥ (OBC) OA ⊥ BC.
Mặt khác ta có AM ⊥ BC nên ta suy ra BC ⊥ (OAM) BC ⊥ OM
Chứng minh tương tự ta được AC ⊥ OM. Do đó OM ⊥ (ABC).
Ta chọn = (1; 2; 2). Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) + 2(y - 2) + 2(z - 2) = 0 x + 2y + 2z - 9 = 0
Chọn D
Câu 7:
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình (m2 - 2m)x + y + (m - 1)z + m2 + m = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) song song với trục Ox?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có = (m2 - 2m; 1; m - 1). Mặt phẳng (P) song song với trục Ox khi và chỉ khi
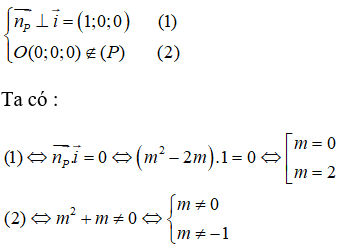
Từ đó ta được m=2.
Vậy đáp án B là đáp án đúng.
Câu 8:
Trong không gian Oxyz, cho hai mặt phẳng (P): x + 2y - 2z + 1 = 0, (Q): 2x + 4y + az + b = 0. Tìm a và b sao cho khoảng cách giữa hai mặt phẳng đó bằng 1.
 Xem đáp án
Xem đáp án
Đáp án B
Muốn khoảng cách giữa hai mặt phẳng (P) và (Q) lớn hơn 0 thì trước hết hai mặt phẳng đó phải song song (nếu hai mặt phẳng đó trùng nhau hoặc cắt nhau thì khoảng cách giữa chúng sẽ bằng 0). Do đó ta có:
Câu 9:
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là x2 + y2 + z2 - 2x - 4y + 6z + 5 = 0 và cho mặt phẳng (P) : x - 2y + 3z + 3 = 0. Khẳng định nào dưới đây là đúng ?
 Xem đáp án
Xem đáp án
Đáp án A
Do đó mặt phẳng (P) giao với mặt cầu (S) theo một đường tròn và (P) không đi qua tâm I của (S).
Vậy đáp án đúng là A.
Câu 10:
Trong không gian Oxyz, cho ba điểm thay đổi A(a; 0; 0), B(0; b; 0), C(0; 0; c) trong đó a, b, c khác 0 và thỏa mãn điều kiện 3ab + bc - 2ac = abc . Khoảng cách lớn nhất từ O đến mặt phẳng (ABC) là:
 Xem đáp án
Xem đáp án
Đáp án B
Mặt phẳng (ABC) đi qua 3 điểm A(a; 0; 0); B(0; b; 0) và C(0; 0; c) nên phương trình mặt phẳng (ABC) là:
Câu 11:
Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M() và có một vectơ pháp tuyến = (A; B; C) là:
 Xem đáp án
Xem đáp án
Đáp án C
Phương trình của mặt phẳng (P) đi qua điểm M() và có một vectơ pháp tuyến (A; B; C) là:
A(x - ) + B(y - ) + C(z - ) = 0
Câu 12:
Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M() và có một vectơ pháp tuyến = (-A; B; -C) là:
 Xem đáp án
Xem đáp án
Đáp án B
Phương trình của mặt phẳng (P) đi qua điểm M(-; y0; -z0) và có một vectơ pháp tuyến = (-A; B; -C) là:
-A(x + ) + B(y - ) - C(z + ) = 0
⇔ A(x + ) - B(y - ) + C(z + ) = 0
Câu 13:
Trong không gian Oxyz, cho điểm M(-x0; -y0; z0) và phương trình của mặt phẳng (P): Ax + By + Cz + D = 0. Khoảng cách từ điểm M đến mặt phẳng (P) là:
 Xem đáp án
Xem đáp án
Đáp án B
Khoảng cách từ điểm M đến mặt phẳng (P) là:
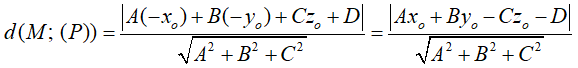
Câu 14:
Trong không gian Oxyz, cho hai mặt phẳng song song (P): Ax + By + Cz + D = 0 và (Q): Ax + By + Cz + D' = 0. M là một điểm di động trên mặt phẳng (P). Khẳng định nào dưới đây có thể sai?
 Xem đáp án
Xem đáp án
Đáp án D
Nếu hai mặt phẳng (P) và (Q) song song với nhau và M thuộc mặt phẳng (P) thì:
+ Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) là 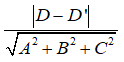
+ Đặc biệt, khoảng cách giữa hai mặt phẳng (P) và (Q) là |D - D'| khi và chỉ khi:
=1
Do đó, mệnh đề D có thể sai.
Câu 15:
Trong các khẳng định dưới đây, khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A(x0; y0; z0) thuộc (P) và biết một vectơ pháp tuyến (A; B; C) của mặt phẳng (P).
Phương trình mặt phẳng (P) khi đó: A(x - ) + B(y - ) + C(z - )= 0
Câu 16:
Trong các khẳng định dưới đây, khẳng định nào sai?
 Xem đáp án
Xem đáp án
Đáp án D
Khẳng định: Nếu hai mặt phẳng (P) và (Q) có hai vectơ pháp tuyến cùng phương thì chúng song song là sai vì khi đó hai mặt phẳng (P) và (Q) có thể trùng nhau.
Câu 17:
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình là x - 2y + 2 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P):
 Xem đáp án
Xem đáp án
Đáp án C
Mặt phẳng (P) có phương trình là x - 2y + 2 = 0. Một vectơ pháp tuyến của mặt phẳng (P): = (1; -2; 0)
Câu 18:
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình là 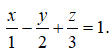
Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P):
 Xem đáp án
Xem đáp án
Đáp án B

Câu 19:
Trong không gian Oxyz, phương trình tổng quát của mặt phẳng (Oxy) là:
 Xem đáp án
Xem đáp án
Đáp án C
Phương trình mặt phẳng (Oxy) là z = 0.
Câu 20:
Trong không gian Oxyz, phương trình tổng quát của mặt phẳng (P) đi qua điểm M(1;-2;3) và song song với mặt phẳng (Oxy) là:
 Xem đáp án
Xem đáp án
Đáp án C
Mặt phẳng (Oxy) có phương trình là: z = 0.
Mặt phẳng này có vecto pháp tuyến là: = (0; 0; 1)
Vì mặt phẳng (P) song song với mặt phẳng (Oxy)
nên mặt phẳng này nhận vecto = = (0; 0; 1) làm vecto pháp tuyến.
Mặt khác (P) đi qua điểm M(1;-2;3) nên (P) có phương trình là:
1.(z - 3) = 0 ⇔ z - 3 = 0
Câu 21:
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;-1 ;3) và song song với mặt phẳng (Q):
 Xem đáp án
Xem đáp án
Đáp án C
Phương trình mặt phẳng (Q) viết lại dưới dạng: 3x - 6y + 2z - 6 = 0
Suy ra đáp án B sai. Trong ba đáp án còn lại chỉ có mặt phẳng ở đáp án C đi qua điểm A.
Câu 22:
Trong không gian Oxyz, lập phương trình mặt phẳng (P) đi qua điểm A(2;-1;-2) và song song với mặt phẳng (Q): 2x - y + 2z = 0
 Xem đáp án
Xem đáp án
Đáp án A
Vì mặt phẳng (P) song song với mặt phẳng (Q): 2x – y + 2z = 0 nên mặt phẳng (P) có dạng: 2x – y + 2z + d = 0 với d khác 0.
Mà mặt phẳng (P) đi qua điểm A(2; -1; -2) nên:
2.2 –(-1) + 2.(-2) + d = 0 nên d = -1
Vậy phương trình mặt phẳng (P) là: 2x – y + 2z – 1= 0
Câu 23:
Trong không gian Oxyz, lập phương trình mặt phẳng (P) đi qua điểm A(-2 ;1 ;-2) và vuông góc với trục Oz.
 Xem đáp án
Xem đáp án
Đáp án D
Do mặt phẳng (P ) vuông góc trục Oz nên mặt phẳng này nhận vecto = (0; 0; 1) làm vecto pháp tuyến.
Lại có:
Điểm A(-2 ; 1 ; -2) thuộc mặt phẳng (P) nên phương trình (P): 0(x + 2) + 0( y - 1) + 1(z + 2)= 0 hay z + 2= 0
Câu 24:
Trong không gian Oxyz, cho hai điểm A(1 ;0 ;-2), B(-1 ;1 ;2). Phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:
 Xem đáp án
Xem đáp án
Đáp án A
Do (P) vuông góc với đường thẳng AB nên mp(P) có một vectơ pháp tuyến là
![]()
Mặt khác (P) đi qua điểm A nên phương trình của mặt phẳng (P) là
-2(x - 1) + (y - 0) + 4(z + 2) = 0 ⇔ 2x - y - 4z - 10 = 0
Câu 25:
Trong không gian Oxyz, cho hai điểm A(1;3;-2), B(1;1;2). Gọi (P) là mặt phẳng trung trực của đoạn thẳng AB. Phương trình của mặt phẳng (P) là:
 Xem đáp án
Xem đáp án
Đáp án A
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB.
Câu 26:
Trong không gian Oxyz, cho điểm M(1;-2;3). Gọi lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz. Trong các khẳng định dưới đây, khẳng định nào sai?
 Xem đáp án
Xem đáp án
Đáp án B
Với điểm M(1;-2;3). Gọi lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz thì tọa độ (1; 0; 0); (0 ;-2; 0) và ( 0; 0; 3).
Phương trình mặt phẳng M1M2M3 là:
Hay
Vậy đáp án A, C, D đúng và B sai.
Câu 27:
Trong không gian Oxyz, cho điểm A(2;-3;4). Lập phương trình mặt phẳng (P) đi qua các hình chiếu vuông góc của điểm A trên các trục tọa độ:
 Xem đáp án
Xem đáp án
Đáp án D
Với điểm A(2;-3;4). Hình chiếu của A trên 3 trục tọa độ lần lượt là:
B(2; 0; 0); C( 0; -3; 0) và D( 0; 0; 4).
Phương trình mặt phẳng (BCD) là:
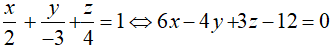
Câu 28:
Trong không gian Oxyz, cho điểm M(1;2;3). Lập phương trình mặt phẳng đi qua M sao cho (P) cắt các trục Ox, Oy, Oz lần lượt tại A, B, C và M là trọng tâm của tam giác ABC
 Xem đáp án
Xem đáp án
Đáp án C
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c). Vì M(1;2;3) là trọng tâm của tam giác ABC nên ta có:
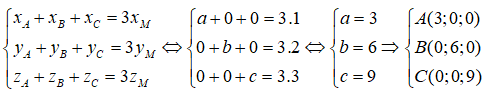
Vậy phương trình của mặt phẳng (P) là:
Câu 29:
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;-2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC
 Xem đáp án
Xem đáp án
Đáp án D
Ta có: OA OB, OC OA (OBC) OA BC
Mặt khác vì AM BC (M là trực tâm tam giác ABC) nên ta suy ra BC (OAM) BC OM
Chứng minh tương tự ta được AC OM. Do đó OM (ABC). Ta chọn: = = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 2(y + 2) + 3(z - 3) = 0 ⇔ x - 2y + 3z - 14 = 0
Câu 30:
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(3;2;1) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O) sao cho tam giác ABC đều. Số mặt phẳng (P) thỏa mãn bài toán là:
 Xem đáp án
Xem đáp án
Đáp án A
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c > 0. Phương trình của mặt phẳng (P) là:
Suy ra: a = b = c = 6. Vậy có một mặt phẳng (P) thỏa mãn bài toán.
Câu 31:
Trong không gian Oxyz, cho mặt phẳng (P) thay đổi nhưng luôn đi qua hai điểm là A(2;0;0), M(1;1;1). Cho (P) cắt các tia Oy, Oz lần lượt tại các điểm B, C (khác O). Viết phương trình mặt phẳng (P) sao cho thể tích của tứ diện OABC nhỏ nhất.
 Xem đáp án
Xem đáp án
Đáp án B
Gọi B(0; b; 0), C(0; 0; c), trong đó b, c > 0.
Ta có: OA = 2; OB = b; OC = c