Trong không gian Oxyz, cho đường thẳng Δ:x−1−2=y2=z−21 và mặt phẳng P:2x−y+z−3=0. Gọi (S) là mặt cầu có tâm I thuộc ∆ và tiếp xúc với (P) tại điểm H1;−1;0. Phương trình của (S) là:

Trong không gian Oxyz, cho đường thẳng delta: x-1/-2 = y/2...

Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Câu trả lời này có hữu ích không?

0

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-2;3;1), B(5;6;2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tính tỉ số $\frac{A M}{B M}$

Xem đáp án » 05/03/2022 2,485

Câu 2:

Trong không gian với hệ tọa độ Oxyz, gọi $(α)$ là mặt phẳng chứa đường thẳng $∆$ có phương trình $\frac{x - 2}{1} = \frac{y - 1}{1} = \frac{z}{2}$ và vuông góc với mặt phẳng $(β) : x + y - 2 z - 1 = 0$ . Giao tuyến của $(α)$ và $(β)$ đi qua điểm nào trong các điểm sau:

Xem đáp án » 05/03/2022 1,368

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 8 x + 2 y + 2 z - 3 = 0$ và đường thẳng $Δ : \frac{x - 1}{3} = \frac{y}{- 2} = \frac{z + 2}{- 1}$ . Mặt phẳng $(α)$ vuông góc với $Δ$ và cắt (S) theo giao tuyến là đường tròn (C) có bán kính lớn nhất. Phương trình $(α)$ là:

Xem đáp án » 05/03/2022 1,129

Câu 4:

Trong không gian với hệ tọa độ Oxyz, mặt phẳng $(α)$ chắn các trục Ox, Oy, Oz lần lượt tại A, B, C sao cho H(3;-4;2) là trực tâm của tam giác ABC. Phương trình mặt phẳng $(α)$ là:

Xem đáp án » 05/03/2022 676

Câu 5:

Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ biết $A (1; 0; 1), B (2; 1; 2), D (2; - 2; 2), A' (3; 0; - 1)$ . Điểm M thuộc cạnh DC. GTNN của tổng các khoảng cách $A M + M C'$ là:

Xem đáp án » 05/03/2022 574

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 6 x - 4 z + 9 - m^{2} = 0$ . Gọi T là tập các giá trị của m để mặt cầu (S) tiếp xúc với mặt phẳng (Oyz). Tích các giá trị của m trong T bằng:

Xem đáp án » 05/03/2022 530

Câu 7:

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song và cách đều hai đường thẳng $d_{1} : \frac{x - 2}{- 1} = \frac{y}{1} = \frac{z}{1}, d {}_{2}: \frac{x}{2} = \frac{y - 1}{- 1} = \frac{z - 2}{- 1}$

Xem đáp án » 05/03/2022 390

Câu 8:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(3;3;-2) và hai đường thẳng $d_{1} : \frac{x - 1}{1} = \frac{y - 2}{3} = \frac{z}{1}, d_{2} : \frac{x - 1}{- 1} = \frac{y - 1}{2} = \frac{z - 2}{4}$ . Đường thẳng d qua M cắt $d_{1}, d_{2}$ lần lượt tại A và B. Tính độ dài đoạn thẳng AB.

Xem đáp án » 05/03/2022 376

Câu 9:

Trong không gian Oxyz, cho hai điểm A(0;-1;2), B(1;1;2) và đường thẳng d: $\frac{x + 1}{1} = \frac{y}{1} = \frac{z - 1}{1}$ . Biết điểm M(a;b;c) thuộc đường thẳng d sao cho tam giác MAB có diện tích nhỏ nhất. Khi đó, giá trị $\frac{x + 1}{1} = \frac{y}{1} = \frac{z - 1}{1}$ bằng:

Xem đáp án » 05/03/2022 354

Câu 10:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;1;2), mặt phẳng (P) qua M cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C (A, B, C có tọa độ dương). Gọi $V_{O A B C}$ là thể tích tứ diện OABC. Khi (P) thay đổi tìm giá trị nhỏ nhất của $V_{O A B C}$

Xem đáp án » 05/03/2022 344

Câu 11:

Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng $(P) : 2 x + 2 y - z - 3 = 0$ và mặt cầu $(S) : {(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 5)}^{2} = 36$ . Gọi $Δ$ là đường thẳng đi qua E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của $Δ$ là:

Xem đáp án » 05/03/2022 319

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng $Δ : \frac{x}{1} = \frac{y + 3}{1} = \frac{z}{2}$ . Biết rằng mặt cầu (S) có bán kính bằng $2 \sqrt{2}$ và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính bằng 2. Tìm tọa độ của điểm I.

Xem đáp án » 05/03/2022 294

Câu 13:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm $A (2; 3; 0), B (0; - \sqrt{2}, 0), M (\frac{2}{5}; - \sqrt{2}; - \frac{2}{5})$ và đường thẳng $d : \{\begin{matrix} x = t \\ y = 0 \\ z = 2 - t \end{matrix}$ . Điểm C thuộc d sao cho chu vi tam giác ABC là nhỏ nhất thì độ dài CM bằng

Xem đáp án » 05/03/2022 281

Câu 14:

Trong không gian Oxyz, cho điểm S(-2;1;-2) nằm trên mặt cầu $(S) : x^{2} + y^{2} + z^{2} = 9$ . Từ điểm S kẻ dây cung SA, SB, SC với mặt cầu (S) có độ dài bằng nhau và đôi một tạo với nhau góc $60 °$ . Dây cung AB có độ dài bằng:

Xem đáp án » 05/03/2022 275

Xem thêm các câu hỏi khác »

LÝ THUYẾT

1. Hệ tọa độ trong không gian

1.1. Tọa độ của điểm và của vecto

1.1.1. Hệ tọa độ

Trong không gian, xét ba trục tọa độ x’Ox; y’Oy; z’Oz vuông góc với nhau từng

đôi một và chung một điểm gốc O. Gọi $\vec{i}; \vec{j}; \vec{k}$ lần lượt là các vectơ đơn vị, trên các trục x’Ox; y’Oy; z’Oz.

Hệ ba trục như vậy gọi là hệ trục tọa độ Đề- các vuông góc Oxyz trong không gian,

hay đơn giản gọi là hệ trục tọa độ Oxyz.

Điểm O được gọi là gốc tọa độ.

Các mặt phẳng (Oxy); (Oyz); (Ozx) đôi một vuong góc với nhau được gọi là các mặt phẳng tọa độ.

Không gian với hệ tọa độ Oxyz còn gọi là không gian Oxyz.

- Vì $\vec{i}; \vec{j}; \vec{k}$ là các vecto đơn vị đôi một vuông góc với nhau nên:

${\vec{i}}^{2} = {\vec{j}}^{2} = {\vec{k}}^{2} = 1$ .

1.1.2. Tọa độ của một điểm

- Trong không gian Oxyz, cho một điểm M tùy ý. Vì ba vecto $\vec{i}; \vec{j}; \vec{k}$ không đồng

phẳng nên có một bộ ba số (x; y; z) duy nhất sao cho:

$\vec{O M} = x . \vec{i} + y . \vec{j} + z . \vec{k}$

- Ngược lại, với bộ ba số (x; y; z) ta có một điểm M duy nhất trong không gian thỏa mãn hệ thức $\vec{O M} = x . \vec{i} + y . \vec{j} + z . \vec{k}$ .

- Ta gọi bộ ba số (x; y; z) là tọa độ của điểm M đối với hệ trục tọa độ Oxyz đã cho và viết: M = ( x; y; z) hoặc M (x; y; z).

1.1.3. Tọa độ của vecto

- Trong không gian Oxyz cho vecto $\vec{a}$ , khi đó luôn tồn tại duy nhất bộ ba số (a₁; a₂ ; a₃) sao cho $\vec{a} = a_{1} . \vec{i} + a_{2} . \vec{j} + a_{3} . \vec{k}$ .

Ta gọi bộ ba số (a₁; a₂ ; a₃) là tọa độ của vecto đối với hệ tọa độ Oxyz cho trước $\vec{a}$ và viết $\vec{a}$ = (a₁; a₂ ; a₃) hoặc $\vec{a}$ (a₁; a₂ ; a₃).

- Nhận xét : Trong hệ tọa độ Oxyz, tọa độ của điểm M chính là tọa độ của vecto $\vec{O M}$ .

Ta có: M(x; y; z) $\Leftrightarrow \vec{O M} (x; y; z)$

1.2. Biểu thức tọa độ của các phép toán của vecto

- Định lí: Trong không gian Oxyz, cho hai vecto

$\vec{a} = (a_{1}; a_{2}; a_{3}), \vec{b} = (b_{1}; b_{2}; b_{3}), k \in R$ , ta có:

a) $\vec{a} + \vec{b} = (a_{1} + b_{1}; a_{2} + b_{2}; a_{3} + b_{3})$

b) $\vec{a} - \vec{b} = (a_{1} - b_{1}; a_{2} - b_{2}; a_{3} - b_{3})$ ;

c) $k \vec{a} = (k a_{1}; k a_{2}; k a_{3})$ .

Ví dụ 1. Cho $\vec{u} (2; - 3; 4); \vec{v} (4; - 2; 0)$

a) Tính $\vec{u} + \vec{v}$ ;

b) $2 \vec{v}$ ;

c) $\vec{u} - 2 \vec{v}$ .

Lời giải:

a) $\vec{u} + \vec{v} = (2 + 4; - 3 - 2; 4 + 0) = (6; - 5; 4)$ ;

b) Ta có: $2 \vec{v}$ = ( 2.4; 2. (-2); 2.0) = ( 8; - 4; 0).

c) Ta có: $\vec{u} - 2 \vec{v}$ = ( 2 – 8; -3 + 4; 4 - 0) = (- 6; 1; 4)

- Hệ quả:

a) Cho hai vecto $\vec{a} = (a_{1}; a_{2}; a_{3}), \vec{b} = (b_{1}; b_{2}; b_{3})$ , ta có:

$\vec{a} = \vec{b} \Leftrightarrow {\begin{matrix} a_{1} = b_{1} \\ a_{2} = b_{2} \\ a_{3} = b_{3} \end{matrix}$ .

b) Vecto $\vec{0}$ có tọa độ ( 0; 0; 0).

c) Với $\vec{b} \neq \vec{0}$ thì hai vecto $\vec{a}; \vec{b}$ cùng phương khi và chỉ khi tồn tại số k sao cho:

$\vec{a} = k \vec{b} (k \in R)$

$\Leftrightarrow {\begin{matrix} a_{1} = k b_{1} \\ a_{2} = k b_{2} \\ a_{3} = k b_{3} \end{matrix} \Leftrightarrow \frac{a_{1}}{b_{1}} = \frac{a_{2}}{b_{2}} = \frac{a_{3}}{b_{3}}, (b_{1}, b_{2}, b_{3} \neq 0)$

d) Cho $A (x_{A}; y_{A}; z_{A}), B (x_{B}; y_{B}; z_{B})$

+ $\vec{A B} = (x_{B} - x_{A}; y_{B} - y_{A}; z_{B} - z_{A})$

+ Toạ độ trung điểm M của đoạn thẳng AB: $M (\frac{x_{A} + x_{B}}{2}; \frac{y_{A} + y_{B}}{2}; \frac{z_{A} + z_{B}}{2})$

Ví dụ 2. Cho $\vec{u} (2 m; 3; - 1); \vec{v} (4; 3; n - 2)$ . Tìm m và n để $\vec{u} = \vec{v}$

Lời giải:

Để $\vec{u} = \vec{v}$

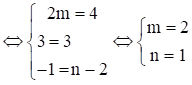
Ôn tập Toán 12 Chương 3 Hình học (ảnh 1)

Vậy m = 2 và n = 1.

Ví dụ 3. Các cặp vecto sau có cùng phương không?

a) $\vec{u} (2; 3; 7); \vec{v} (- 4; - 6; 14)$ ;

b) $\vec{a} (1; 0; 2); \vec{b} (- 3; 0; - 6)$ .

Lời giải:

a) Ta thấy $\frac{2}{- 4} = \frac{3}{- 6} \neq \frac{7}{14}$

Do đó, hai vecto trên không cùng phương.

b) Ta thấy: $\vec{b} = - 3 \vec{a}$ nên hai vecto trên cùng phương.

Ví dụ 4. Cho hai điểm A( - 3; 4; 0) và B( -1; 0; 8).

a) Tính $\vec{A B}$ ;

b) Tìm tọa độ trung điểm M của AB.

Lời giải:

a) Ta có: $\vec{A B}$ = ( -1 + 3; 0 - 4; 8 -0) = ( 2; -4; 8).

b) Tọa độ trung điểm M của AB là:

${\begin{matrix} x_{M} = \frac{- 3 + (- 1)}{2} = - 2 \\ y_{M} = \frac{4 + 0}{2} = 2 \\ z_{M} = \frac{0 + 8}{2} = 4 \end{matrix} \Rightarrow M (- 2; 2; 4)$

1.3. Tích vô hướng.

1.3.1. Biểu thức tọa độ của tích vô hướng.

- Định lí:

Trong không gian Oxyz, tích vô hướng của hai vecto $\vec{a} = (a_{1}; a_{2}; a_{3}), \vec{b} = (b_{1}; b_{2}; b_{3})$ được xác định bởi công thức:

$\vec{a} . \vec{b} = a_{1} . b_{1} + a_{2} . b_{2} + a_{3} . b_{3}$

Ví dụ 5. Cho $\vec{a} (1; - 3; 4); \vec{b} (1; 2; 1)$ . Tính $\vec{a} . \vec{b}$ ?

Lời giải:

Ta có: $\vec{a} . \vec{b}$ = 1.1 + ( -3). 2 + 4.1 = -1

1.3.2. Ứng dụng

a) Độ dài của một vecto.

Cho vecto $\vec{a} = (a_{1}; a_{2}; a_{3})$ .

Ta biết rằng: ${| \vec{a} |}^{2} = {\vec{a}}^{2}$ hay $| \vec{a} | = \sqrt{{\vec{a}}^{2}}$ . Do đó, $| \vec{a} | = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{2}^{2}}$

b) Khoảng cách giữa hai điểm.

Trong khong gian Oxyz, cho hai điểm A(x_A ; y_A ; z_A)

và B(x_B; y_B ; z_B). Khi đó, khoảng cách giữa hai điểm A và B chính là độ dài của

vecto $\vec{A B}$ . Do đó, ta có:

$A B = | \vec{A B} | = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2} + {(z_{B} - z_{A})}^{2}}$ .

c) Góc giữa hai vecto.

Nếu $φ$ là góc góc giữa hai vecto $\vec{a} = (a_{1}; a_{2}; a_{3})$ và $\vec{b} = (b_{1}; b_{2}; b_{3})$ với $\vec{a}; \vec{b} \neq \vec{0}$ thì $\cos (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{| \vec{a} | . | \vec{b} |} = \frac{a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}}{\sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}} . \sqrt{b_{1}^{2} + b_{2}^{2} + b_{3}^{2}}}$

Từ đó, suy ra $\vec{a} ⊥ \vec{b} \Leftrightarrow a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} = 0$

Ví dụ 6. Cho tam giác ABC có A(2; 3; 1); B( 2; 1; 0); C( 0; -1; 2).

a) Tính AB; AC

b) Tính cosin của góc A.

Lời giải:

a) Ta có:

$\begin{matrix} A B = \sqrt{{(2 - 2)}^{2} + {(1 - 3)}^{2} + {(0 - 1)}^{2}} = \sqrt{5} \\ A C = \sqrt{{(0 - 2)}^{2} + {(- 1 - 3)}^{2} + {(2 - 1)}^{2}} = \sqrt{21} \end{matrix}$

b) Ta có: $\vec{A B} (0; - 2; - 1); \vec{A C} (- 2; - 4; 1)$

Cosin của góc A là:

$\cos A = \cos (\vec{A B}; \vec{A C}) = \frac{0 . (- 2) + (- 2) . (- 4) + (- 1) .1}{\sqrt{5} . \sqrt{21}} = \frac{7}{\sqrt{105}}$

1.4. Phương trình mặt cầu

- Định lí.

Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c) bán kính r có phương trình là:

( x – a)² + (y – b)² + (z – c)² = r²

- Nhận xét. Phương trình mặt cầu nói trên có thể viết dưới dạng:

x² + y² + z² – 2ax – 2by – 2cz + d = 0 với d = a² + b² + c² – r²

Từ đó, ta chứng minh được rằng phương trình dạng:

x² + y² + z² + 2Ax + 2By + 2Cz + D = 0 với điều kiện A² + B² + C² – D > 0 là phương trình mặt cầu có tâm I( -A; -B; - C) có bán kính $r = \sqrt{A^{2} + B^{2} + C^{2} - D}$ .

Ví dụ 7. Tìm tâm và bán kính của mặt cầu có phương trình sau đây:

a) x² + y² + z² – 4x + 2y - 1 = 0;

b) x² + y² + z² – 8x – 2y + 2z + 2 = 0

Lời giải:

a) Ta có: a = 2; b = -1; c = 0; d = -1

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Trong không gian Oxyz, cho đường thẳng Δ:x−1−2=y2=z−21 và mặt phẳng P:2x−y+z−3=0. Gọi (S) là mặt cầu có tâm I thuộc ∆ và tiếp xúc với (P) tại điểm H1;−1;0. Phương trình của (S) là:

A. x−32+y+22+z−12=36

B. x−32+y−22+z−12=36

C. x−32+y+22+z−12=6

D. x−32+y−22+z−12=6

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-2;3;1), B(5;6;2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tính tỉ số AMBM

Trong không gian Oxyz, cho đường thẳng $Δ : \frac{x - 1}{- 2} = \frac{y}{2} = \frac{z - 2}{1}$ và mặt phẳng $(P) : 2 x - y + z - 3 = 0$ . Gọi (S) là mặt cầu có tâm I thuộc $∆$ và tiếp xúc với (P) tại điểm $H (1; - 1; 0)$ . Phương trình của (S) là:

A. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 36$

B. ${(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 36$

C. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 6$

D. ${(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 6$

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-2;3;1), B(5;6;2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tính tỉ số $\frac{A M}{B M}$