Tìm điểm M biểu diễn số phức
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
nên điểm biểu diễn là
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
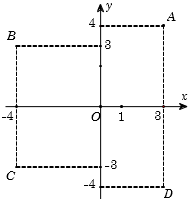
Trong mặt phẳng tọa độ (hình vẽ bên). Số phức được biểu diễn bởi điểm nào trong các điểm A, B, C, D?
Gọi M, N lần lượt là các điểm biểu diễn số phức và . Chọn câu đúng:
1. Số i.
Số i là số thỏa mãn: i2 = –1.
2. Định nghĩa số phức
Mỗi biểu thức dạng a + bi , trong đó R; i2 = –1 được gọi là một số phức.
Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.
Tập hợp các số phức kí hiệu là .
Ví dụ 1. Các số sau là những số phức: 2 – 3i; –8 + 4i; .
Ví dụ 2. Số phức 6 – i có phần thực là 6, phần ảo là – 1.
– Định nghĩa : Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :
a + bi = c + di a = c và b = d.
Ví dụ 3. Tìm các số thực x và y biết :
(2x – 1) + (y – 2)i = 3 + (4 – y)i
Lời giải:
Ta có : (2x – 1) + (y – 2)i = 3 + (4 – y)i
Vậy x = 2 và y = 3.
– Chú ý :
a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0: a = a + 0i.
Như vậy, mỗi số thực cũng là một số phức. Ta có : .
b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi
Đặc biệt : i = 0 + 1.i
Số i được gọi là đơn vị ảo.
Ví dụ 4. Số phức z có phần thực là và phần ảo là là .
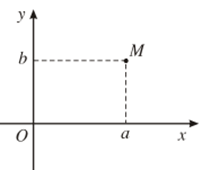
Điểm M(a ; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.
Ví dụ 5.
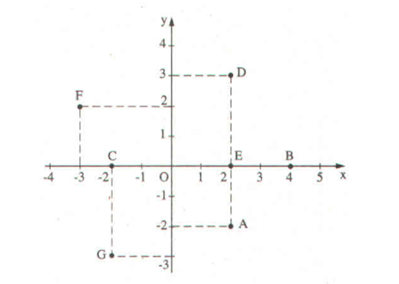
Điểm A biểu diễn số phức 2 – 2i
Điểm B biểu diễn số phức 4.
Điểm C biểu diễn số phức – 2.
Điểm D biểu diễn số phức 2 + 3i.
Điểm E biểu diễn số phức 2.
Điểm F biểu diễn số phức – 3 + 2i.
Điểm G biểu diễn số phức –2 – 3i.
5. Mô đun của số phức.
Giả sử số phức z = a + bi được biểu diễn bởi điểm M(a ; b) trên mặt phẳng tọa độ.
Độ dài của vecto được gọi là môđun của số phức z và kí hiệu là |z|.
Vậy hay .
Ta thấy :.
Ví dụ 6.
6. Số phức liên hợp
– Định nghĩa : Cho số phức z = a + bi. Ta gọi a – bi là số phức liên hợp của z và kí hiệu là
Ví dụ 7.
Nếu z = – 3 + 5i thì
Nếu z = – 4 + 4i thì
– Nhận xét :
+ Trên mặt phẳng tọa độ các điểm biểu diễn z và đối xứng nhau qua trục Ox.
+ Từ định nghĩa ta có: