Tổng tất cả nghiệm của phương trình \(\sin 2x + 4\sin x - 2\cos x - 4 = 0\) trên đoạn \(\left[ {0;100\pi } \right]\).
A.\(100\pi .\)
B.\(25\pi .\)
C.\(2475\pi .\)
D. \(2476\pi .\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C.
Ta có \(\sin 2x + 4\sin x - 2\cos x - 4 = 0 \Leftrightarrow \left( {\sin 2x + 4\sin x} \right) - 2\left( {\cos x + 2} \right) = 0\)
\( \Leftrightarrow 2\sin x\left( {\cos x + 2} \right) - 2\left( {\cos x + 2} \right) = 0\)
\( \Leftrightarrow \left( {2\sin x - 2} \right)\left( {\cos x + 2} \right) = 0\).
\( \Leftrightarrow \sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi ,\left( {k \in \mathbb{Z}} \right).\)
Trên đoạn \(\left[ {0;100\pi } \right]\) ta có \(0 \le x \le 100\pi .\)
\( \Leftrightarrow 0 \le \frac{\pi }{2} + k2\pi \le 100\pi \Leftrightarrow \frac{{ - 1}}{4} \le k \le \frac{{199}}{4}\)
Với \(k \in \mathbb{Z}\) ta có \(k \in \left\{ {0;1;2;....;48;49} \right\}.\)
Vậy tổng các nghiệm của phương trình trên đoạn \(\left[ {0;100\pi } \right]\) là
\(S = \frac{\pi }{2} + \left( {\frac{\pi }{2} + 2\pi } \right) + \left( {\frac{\pi }{2} + 2.2\pi } \right) + \left( {\frac{\pi }{2} + 3.2\pi } \right) + ... + \left( {\frac{\pi }{2} + 49.2\pi } \right)\)
\( = \frac{{50\pi }}{2} + \left( {1 + 2 + ... + 49} \right).2\pi = 2475\pi .\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Đội văn nghệ của lớp 12A có 5 học sinh nam và 7 học sinh nữ. Có bao nhiêu cách chọn ra 2 học sinh của đội văn nghệ sao cho 2 học sinh có 1 học sinh nam và 1 học sinh nữ.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(O\) cạnh \[a.\] Biết \(SA = SB = SC = a.\) Đặt \(SD = x\left( {0 < x < a\sqrt 3 } \right).\) Tính \(x\) theo \(a\) sao cho \(AC.SD\) đạt giá trị lớn nhất.
Số đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{\sqrt {x + 4} - 2}}{{{x^2} - x}}\) là
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ:
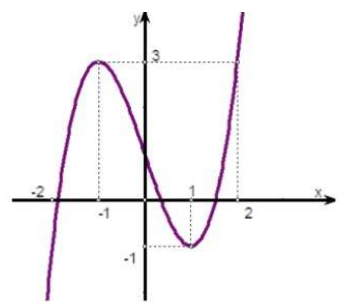
Gọi \(S\) là tập các giá trị nguyên của tham số \(m\) để phương trình \(f\left( {4\left| {\sin x} \right| + m} \right) - 3 = 0\) có đúng 12 nghiệm phân biệt thuộc nửa khoảng \(\left( {0;4\pi } \right].\) Tổng các phần tử của \(S\) bằng
Cho hàm số \(f\left( x \right) = {x^5} + 3{x^3} - 4m.\) Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt[3]{{f\left( x \right) + m}}} \right) = {x^3} - m\) có nghiệm thuộc đoạn \(\left[ {1;2} \right]?\)
Gọi \(S\) là tập hợp các số tự nhiên có bốn chữ số đôi một khác nhau lập từ các số \(0;1;2;3;4;5;6;7.\) Chọn ngẫu nhiên 1 số từ tập hợp \(S.\) Tính xác suất để số được chọn có đúng 2 chữ số chẵn.
Tập nghiệm của bất phương trình \({6.9^x} - {12.6^x} + {6.4^x} \le 0\) có dạng \(S = \left[ {a;b} \right].\) Giá trị của biểu thức \({a^2} + {b^2}\) bằng
Hệ số của \({x^5}\) trong khai triển \({x^2}{\left( {x - 2} \right)^5} + {\left( {2x - 1} \right)^6}\) bằng
Phương trình tiệm cận ngang của đồ thị hàm số \(y = \frac{{4 - 3x}}{{4x + 5}}\) là
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
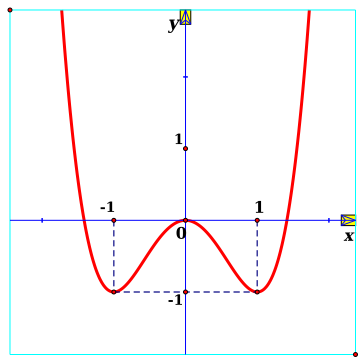
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ. Phương trình \(f\left( {2 - f\left( x \right)} \right) = 0\) có tất cả bao nhiêu nghiệm thực phân biệt?
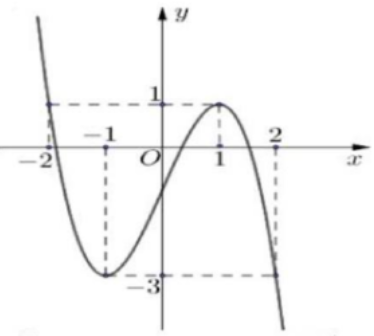
Gọi \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\) là hai nghiệm của phương trình \({3^{2x - 1}} - {4.3^x} + 9 = 0.\) Giá trị của biểu thức \(P = {x_2} - 2{x_1}\) bằng </>
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,SA\) vuông góc với mặt đáy và \(SA = a\sqrt 2 .\) Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng