Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, , cạnh bên SA vuông góc với mặt đáy và SA=a. Tính thể tích V của khối chóp S.ABC .
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án là D.
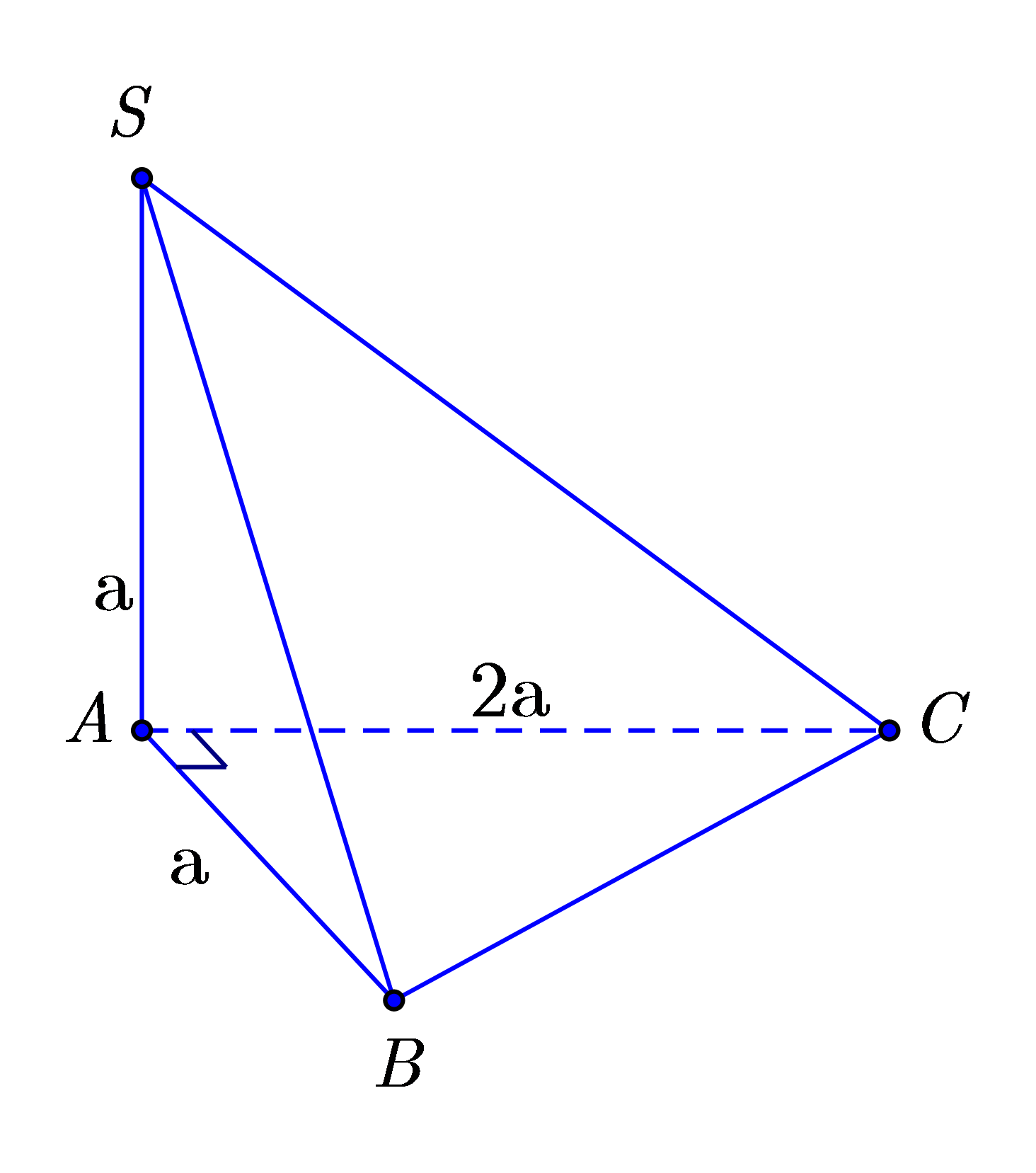
Ta có:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ?
Xét tính đúng sai của các mệnh đề sau (với a, b, c, d là các hằng số).
(I): Giá trị cực đại của hàm số luôn lớn hơn giá trị cực tiểu của nó.
(II): Hàm số luôn có ít nhất một cực trị
(III): Giá trị cực đại của hàm số luôn lớn hơn mọi giá trị của hàm số đó trên tập xác định.
(IV): Hàm số không có cực trị.
Số mệnh đề đúng là:
Tìm tất cả các giá trị thực của m để đồ thị hàm số có hai đường tiệm cận ngang.
Cho hàm số . Đường thẳng cắt (C) tại 2 điểm phân biệt M, N và MN nhỏ nhất khi
Thầy Tâm cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng . Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000 đồng/. Khi đó, kích thước của hồ nước như thể nào để chi phí thuê nhân công mà thầy Tâm phải trả thấp nhất: