Một tổ gồm 9 học sinh nam và 3 học sinh nữ. Cần chia tổ đó thành 3 nhóm, mỗi nhóm 4 người để đi làm 3 công việc khác nhau. Tính xác suất để mỗi nhóm đi làm việc thì có đúng 1 nữ.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Số cách chia tổ thành 3 nhóm đi làm 3 công việc khác nhau là
Với công việc thứ nhất có cách chọn 3 nam, 1 nữ.
Với công việc thứ nhất có cách chọn 3 nam, 1 nữ.
Với công việc thứ nhất có cách chọn 3 nam, 1 nữ.
Vậy xác suất cần tính là
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm số hoán vị của n phần tử trong đó có 2 phần tử a và b không đứng cạnh nhau.
Cho phương trình . Với giá trị nào của m thì phương trình đã cho có nghiệm?
Cho đường thẳng Hình chiếu vuông góc của d lên mặt phẳng (Oxy) là đường thẳng
Cho hàm số có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
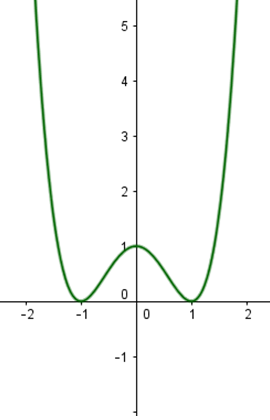
Viết công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục tung và đường thẳng x = 2
Cho và D nằm trên Oy và thể tích tứ diện ABCD bằng 3. Tọa độ của D là
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh bằng 2a, SA vuông góc với đáy, góc giữa SC với mặt đáy bằng . Tính thể tích V của khối chóp S.ABCD.
Cho hàm số Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm A(0;1) khi m bằng
Cho hai điểm . Đường thẳng MN cắt mặt phẳng Oxz tại điểm I. Điểm I chia đoạn thẳng MN theo tỉ số