
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Cách 1: Gọi , với . Ta có
.
Đặt . Suy ra
Ta có
Suy ra
Dấu bằng xảy ra khi .
Cách 2: Sử dụng công thức diện tích hình phẳng giới hạn bởi và trục hoành là .
Tổng quát với và thì ta lập phương trình hoành độ giao điểm .
Áp dụng .Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian , cho hai điểm và . Mặt phẳng trung trực của đoạn thẳng có phương trình là
Trong không gian , hình chiếu vuông góc của điểm trên mặt phẳng có tọa độ là
Cho hàm số có đồ thị như hình vẽ bên dưới.
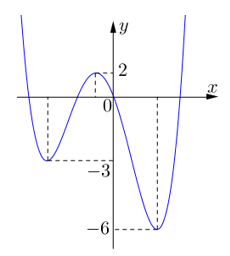
Gọi là tập tất cả các giá trị nguyên dương của tham số để hàm số có đúng điểm cực trị. Số phần tử của là
Cho số phức ; biết rằng các điểm biểu diễn hình học của số phức ; và tạo thành một tam giác có diện tích bằng . Mô đun của số phức bằng
Trong không gian với hệ trục tọa độ , cho điểm và mặt phẳng có phương trình: . Phương trình mặt cầu có tâm và tiếp xúc với mặt phẳng là
Cho hình chóp có đáy là hình chữ nhật có , vuông góc với mặt phẳng , . Gọi là góc giữa đường thẳng và mp . Khi đó bằng bao nhiêu?
Cho mặt cầu và các điểm , . Gọi là một điểm bất kỳ thuộc mặt cầu . Tìm giá trị nhỏ nhất của biểu thức ?