A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Phương pháp:
* Phương pháp xét sự đồng biến, nghịch biến của các hàm số:
- Bước 1: Tìm tập xác định, tính
- Bước 2: Tìm các điểm tại đó hoặc không xác định
- Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên
- Bước 4: Kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Cách giải:
+) ta có Hàm số đồng biến trên các khoảng
+) : Hàm số đồng biến trên .
+) : Hàm số đồng biến trên .
+) Hàm số đồng biến trên .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
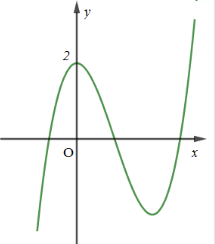
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
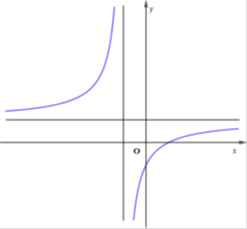
Cho hàm số liên tục trên khoảng và . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm khi và chỉ khi .
(2) Nếu hàm số có đạo hàm và có đạo hàm cấp hai tại điểm thỏa mãn điều kiện thì điểm không phải là điểm cực trị của hàm số .
(3) Nếu đổi dấu khi x qua điểm thì điểm là điểm cực tiểu của hàm số
(4) Nếu hàm số có đạo hàm và có đạo hàm cấp hai tại điểm thỏa mãn điều kiện thì điểm là điểm cực tiểu của hàm số