A. 3√6V
B. 3√2V
C. 3√4V
D. 3√V
Giải bởi Vietjack
Đáp án C
Phương pháp:
Thể tích hình lăng trụ V = Sh
Diện tích toàn phần của lăng trụ: Stp=Sxq+2.Sđáy
Cách giải:
Giả sử hình lăng trụ có đáy là tam giác đều cạnh a, có chiều cao h.
Diện tích đáy: S=a2√34
Tổng diện tích các mặt xung quanh là: Sxq = 3.(a.h)
Thể tích V=a2√34.h⇒h=4V√3a2
Diện tích toàn phần:
Stp=3a.h+2.a2√34=3a.4V√3a2+a2√32=4√3Va+a2√32=2√3Va+2√3Va+a2√32≥33√2√3Va.2√3Va.a2√32=3√3.3√2V2
( áp dụng bất đẳng thức Cô- si cho 3 số dương)
Dấu “=” xảy ra khi và chỉ khi 2√3Va=a2√32⇒a3=4V⇔a=3√4VGói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
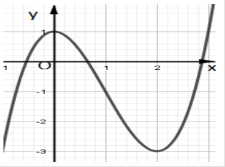
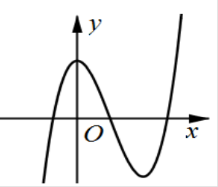
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Cho đường tròn quay quanh một đường thẳng đi qua tâm đường tròn đó một góc 3600 ta được hình gì?
