Viết số phức sau dạng lượng giác:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A.
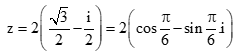
![]()
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Các điểm biểu diễn các số phứctrong mặt phẳng tọa độ, nằm trên đường thẳng có phương trình là:
Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện phần thực của z nằm trong đoạn [-1;3] là:
Tìm số thực x,y để hai số phức z1 = 9y2 - 4 - 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
Tập hợp các điểm biểu diễn số phức . Tập hợp các điểm biểu diễn số phức z là đường tròn nào sau đây ?