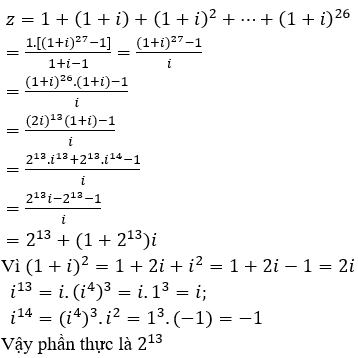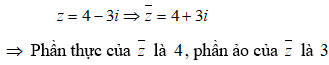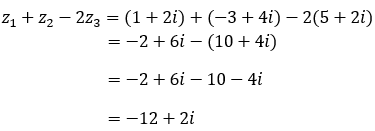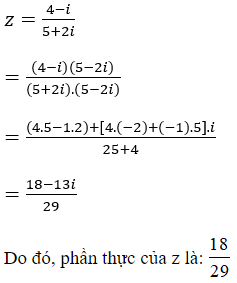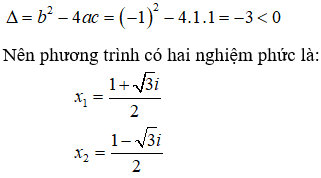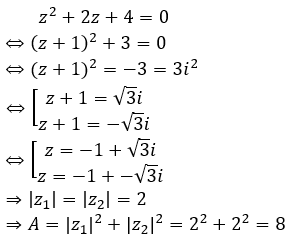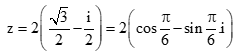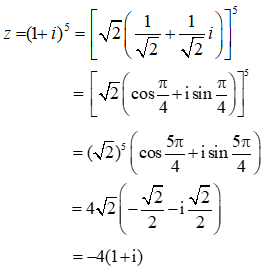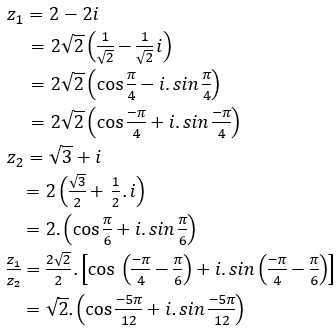Đề kiểm tra 45 phút Toán 12 Chương 4 Giải tích có đáp án (Đề 4)
-
1640 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho số phức Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Chọn C.
Ta có: z = i – 1 = - 1 + i .
Phần thực của z là -1, phần ảo của z là 1, môđun của z bằng
![]()
Số phức liên hợp của số phức z là
Câu 3:
Điểm M(-1;3) là điểm biểu diễn của số phức
 Xem đáp án
Xem đáp án
Chọn A.
z = a + bi có điểm biểu diễn là M(a;b).
Ta suy ra, điểm M(-1;3) biểu diễn số phức z = -1 + 3i
Câu 4:
Các điểm biểu diễn các số phứctrong mặt phẳng tọa độ, nằm trên đường thẳng có phương trình là:
 Xem đáp án
Xem đáp án
Chọn D
Các điểm biểu diễn số phức z = 3 + bi(b ∈ R) có dạng M(3;b) nên nằm trên đường thẳng x = 3
Câu 5:
Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện phần thực của z nằm trong đoạn [-1;3] là:
 Xem đáp án
Xem đáp án
Chọn A.
Điểm biểu diễn các số phức z có phần thực z nằm trong đoạn [-1;3] có dạng M(a;b) với -1 ≤ a ≤ 3
Câu 10:
Tìm số phức z thỏa mãn hệ thức
 Xem đáp án
Xem đáp án
Chọn A.
![]()
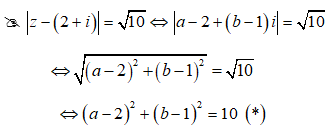
![]()
![]()
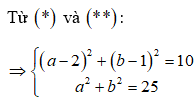
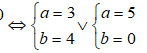
Vậy có hai số phức thỏa mãn là: z = 3+ 4i hoặc z = 5.
Câu 11:
Tập hợp các điểm biểu diễn số phức . Tập hợp các điểm biểu diễn số phức z là đường tròn nào sau đây ?
 Xem đáp án
Xem đáp án
Chọn D.
Tập hợp các điểm biểu diễn số phức 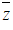
Mà tập hợp các điểm biểu diễn số phức z đối xứng với tập hợp các điểm biểu diễn số phức 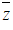
Câu 13:
Tính căn bậc hai của số phức ra kết quả:
 Xem đáp án
Xem đáp án
Chọn B.
Giả sử w = x + yi (x, y ∈ R) là một căn bậc hai của số phức z = 8 + 6i.
![]()
![]()
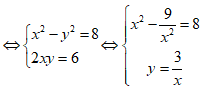
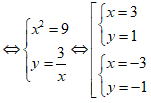
Do đó z có hai căn bậc hai là 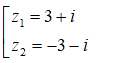
Câu 15:
Trong tập số phức, giá trị của m để phương trình bậc hai có tổng bình phương hai nghiệm bằng -4i là:
 Xem đáp án
Xem đáp án
Chọn A.
Gọi z1, z2 là hai nghiệm của phương trình.
Theo Viet, ta có:
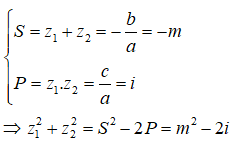
Để tổng bình phương hai nghiệm bằng – 4i thì:
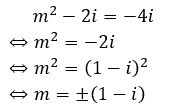
Câu 16:
Tìm số thực x,y để hai số phức z1 = 9y2 - 4 - 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
 Xem đáp án
Xem đáp án
Chọn D.
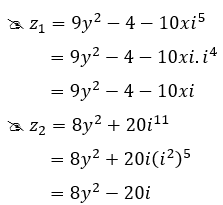
![]()
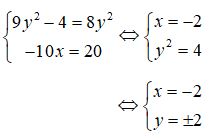
Câu 18:
Cho số phức Phần thực của số phức z là
 Xem đáp án
Xem đáp án
Chọn A.
Ta có: z = 1 + (1 + i) + (1 + i)2 + .... (1 + i)26 là tổng của cấp số nhân với số hạng đầu u1 = 1, công bội q = 1 + i nên: