Cho hàm số $y=x^{e-3}$. Trong các kết luận sau, kết luận nào sai?

I. Khái niệm

– Hàm số $y=x^{\alpha }$, với $\alpha \mathrm{ }\in R$, được gọi là hàm số lũy thừa.

Ví dụ 1. Các hàm số $y=x^{\sqrt{3}\mathrm{ }+1};y=\frac{1}{x^2};y=x^5;y=x^{\pi \mathrm{ }-3}$ là những hàm số lũy thừa.

– Chú ý:

Tập xác định của hàm số lũy thừa $y=x^{\alpha }$ tùy thuộc vào giá trị của α. Cụ thể:

+ Với α nguyên dương, tập xác định là R.

+ Với α nguyên âm hoặc bằng 0; tập xác định là $R\backslash 0$.

+ Với α không nguyên, tập xác định là $(0;+\mathrm{\infty })$.

II. Đạo hàm của hàm số lũy thừa

– Hàm số lũy thừa $y=x^{\alpha }(\alpha \mathrm{ }\in R)$ có đạo hàm với mọi x > 0 và ${\left(x^{\alpha }\right)}^{\text{'}}=\alpha .x^{\alpha \mathrm{ }-1}$.

– Ví dụ 2.

a) ${\left(x^{\frac{2}{5}}\right)}^{\text{'}}=\frac{2}{5}.x^{\frac{-3}{5}}$

b) ${\left(x^{\sqrt{7}}\right)}^{\text{'}}=\sqrt{7}.x^{\sqrt{7}\mathrm{ }-1}$.

– Chú ý: Công thức tính đạo hàm của hàm hợp đối với hàm số lũy thừa có dạng:

${\left(u^{\alpha }\right)}^{\text{'}}=\alpha .u^{\alpha \mathrm{ }-1}.u^{\text{'}}$

– Ví dụ 3. Tính đạo hàm của hàm số $y={(2x{}^2+3x-2)}^{\frac{1}{3}}$.

Lời giải:

Ta có:

 $\begin{array}{c}{y}^{\text{'}}=\frac{1}{3}.{(2x{}^2+3x-2)}^{\frac{-2}{3}}.{(2x{}^2+3x-2)}^{\text{'}}=\frac{1}{3}.{(2x{}^2+3x-2)}^{\frac{-2}{3}}.(4x+3).\end{array}$

III. Khảo sát hàm số lũy thừa y = x^α

Tập xác định của hàm số lũy thừa $y=x^{\alpha }$ luôn chứa khoảng $(0;+\mathrm{\infty })$ với $\alpha \mathrm{ }\in R$. Trong trường hợp tổng quát, ta khảo sát hàm số $y=x^{\alpha }$ trên khoảng này (gọi là tập khảo sát).

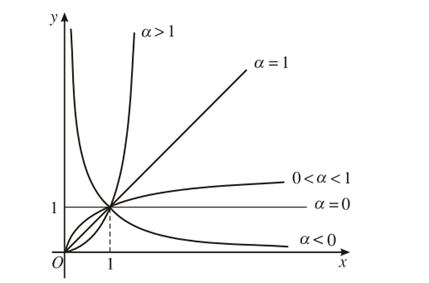
Đồ thị của hàm số lũy thừa y = x^α luôn đi qua điểm (1; 1).

– Chú ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.

Ví dụ 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y=x^{\frac{-2}{5}}$.

Lời giải:
1. Tập xác định: $D=(0;+\mathrm{\infty })$

2. Sự biến thiên.

Chiều biến thiên $y^{\text{'}}=\frac{-2}{5}{x}^{\frac{-7}{5}}$

Ta có: y’ < 0 trên khoảng $D=(0;+\mathrm{\infty })$  nên hàm số đã cho nghịch biến.

Tiệm cận: $\underset{x\to 0^{+}}{lim}y=+\mathrm{\infty };\underset{x\to +\mathrm{\infty }}{lim}y=\mathrm{\hspace{0.17em}\hspace{0.17em}0}$

Đồ thị có tiệm cận ngang là trục hoành và có tiệm cận đứng là trục tung.

Bảng biến thiên

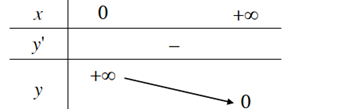
3. Đồ thị

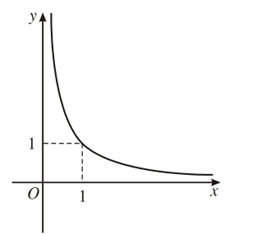
 Bảng tóm tắt các tính chất của hàm số lũy thừa $y=x^{\alpha }$ trên khoảng $(0;+\mathrm{\infty })$.