Cho số phức z thỏa mãn điều kiện .
Tìm giá trị lớn nhất của biểu thức
A. maxT=
B. maxT=8
C. maxT=
D. maxT=4
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Phương pháp: Đưa biểu thức T về dạng biểu thức vector bằng cách tìm các vecto biểu diễn cho các số phức.
Cách giải:
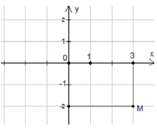
Tập hợp các điểm z thỏa mãn điều kiện ![]() là đường tròn (C) tâm I(1;0) bán kính R=
là đường tròn (C) tâm I(1;0) bán kính R=
![]()
Gọi M là điểm biểu diễn cho số phức z, A(0;-1) là điểm biểu diễn cho số phức -i, B(2;1) là điểm biểu diễn cho số phức 2+i
Dễ thấy A,BC và ![]()
![]() AB là đường kính của đường tròn (C)
AB là đường kính của đường tròn (C)
![]() vuông tại M
vuông tại M
![]()
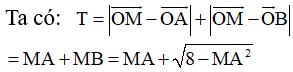
Đặt ![]()
Xét hàm số ![]() trên
trên ![]() ta có:
ta có:
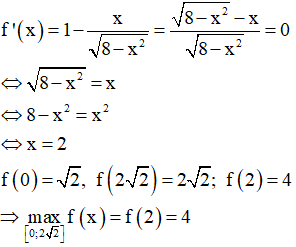
Vậy maxT=4
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho số phức z thỏa mãn z(2-i)+13i=1. Tính mô đun của số phức z.
Cho hai số phức và .
Tính tổng phần thực và phần ảo của số phức .
Gọi S là tập hợp các số thực m sao cho với mỗi có đúng một số phức thỏa mãn và là số thuần ảo. Tính tổng của các phần tử của tập S.
Cho số phức z và w thỏa mãn z+w=3+4i và .
Tìm giá trị lớn nhất của biểu thức .
Cho i là đơn vị ảo. Gọi S là tập hợp các số nguyên dương n có 2 chữ số thỏa mãn là số nguyên dương. Số phần tử của S là
Trong tập các số phức, cho phương trình (1). Gọi là một giá trị của m để phương trình (1) có hai nghiệm phân biệt thỏa mãn Hỏi trong khoảng (0;20) có bao nhiêu giá trị m ?
Cho số phức z có biểu diễn hình học là điểm M ở hình vẽ bên. Khẳng định nào sau đây đúng ?