Xét các số phức z = a + bi(a,b) thỏa mãn điều kiện |z-4-3i| = . Tính P = a + b khi giá trị biểu thức |z+1-3i| + |z-1+i| đạt giá trị lớn nhất.
A. P = 10
B. P = 4
C. P = 6
D. P = 8
Giải bởi Vietjack
Đáp án A.
Gọi M(x;y) là điểm biểu diễn số phức z.
Từ giả thiết, ta có 
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = . Khi đó P = MA + MB, với A(-1;3), B(1;-1)
Ta có: 
Gọi E(0;1) là trung điểm của AB 
Do đó 
mà 
suy ra 
Với C là giao điểm của đường thẳng EI với đường tròn (C).
Vậy 
Dấu “=” xảy ra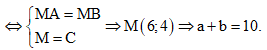 
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Gọi và là hai nghiệm phức của phương trình - 4z + 3 = 0. Giá trị của || + || bằng
Cho hai số phức = 1 - 2i, = 3 + i. Tìm phần thực và ảo của số phức z =
Cho hai số phức = 1 + 2i, = 3 - 2i. Tính mô đun của số phức - 2.
Cho số phức z = 3 - 2i. Tìm điểm biểu diễn của số phức w = z + i.
Cho số phức z thỏa mãn (3+i)z = 13 - 9i. Tìm tọa độ của điểm M biểu diễn z.
Cho số phức z thỏa mãn điều kiện 3 |z-3i+1|5. Tập hợp các điểm biểu diễn của
Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó.
Cho M(1;2) là điểm biểu diễn số phức z. Tìm tọa độ của điểm N biểu diễn số phức w = z + 2.
Gọi là hai nghiệm phức của phương trình + 2z + 1 = 0. Tính P = .
