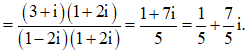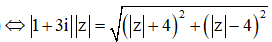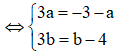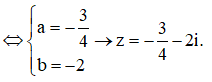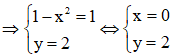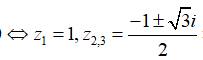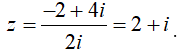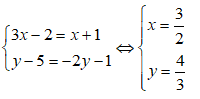25 câu hỏi trắc nghiệm thuộc 225 Bài tập Số phức ôn thi Đại học có lời giải (P5)

Câu 1:

Cho hai số phức $z_{1}, z_{2}$ . Chọn mệnh đề đúng

$A . N ế u | z_{1} | = | z_{2} | t h ì z_{1} = \bar{z_{2}}$

$B . N ế u z_{1} = \bar{z_{2}} t h ì | z_{1} | = | z_{2} |$

$C . N ế u | z_{1} | = | z_{2} | t h ì z_{1} = z_{2}$

$D . N ế u | z_{1} | = | z_{2} |$ thì thì các điểm biểu diễn cho $z_{1}$ và $z_{2}$ tương ứng trên mặt phẳng tọa độ sẽ đối xứng nhau qua gốc tọa độ O

Xem đáp án

Đáp án B

Lấy ví dụ dễ thấy A, C, D sai

Câu 2:

Gọi $z_{1}$ và $z_{2}$ là hai nghiệm phức của phương trình $4 z^{2}$ - 4z + 3 = 0. Giá trị của | $z_{1}$ | + | $z_{2}$ | bằng

$A . 3 \sqrt{2}$

$B . 2 \sqrt{3}$

$C . 3$

$D . \sqrt{3}$

Xem đáp án

Đáp án D.

Ta có $4 z^{2}$ - 4z + 3 = 0

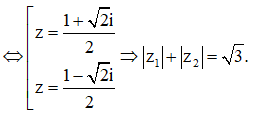
Câu 3:

Cho số phức z = a + bi(a,b $\in ℝ$ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b

A. P = -1

B. P = -5

C. P = 3

D. P = 7

Xem đáp án

Đáp án D.

Đặt z = a + bi

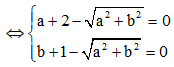
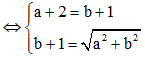
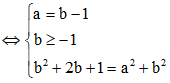
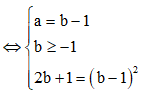
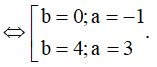
Câu 4:

Xét các số phức z = a + bi(a,b $\in ℝ$ ) thỏa mãn điều kiện |z-4-3i| = $\sqrt{5}$ . Tính P = a + b khi giá trị biểu thức |z+1-3i| + |z-1+i| đạt giá trị lớn nhất.

A. P = 10

B. P = 4

C. P = 6

D. P = 8

Xem đáp án

Đáp án A.

Gọi M(x;y) là điểm biểu diễn số phức z.

Từ giả thiết, ta có

=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = $\sqrt{5}$ . Khi đó P = MA + MB, với A(-1;3), B(1;-1)

Ta có:

Gọi E(0;1) là trung điểm của AB

Do đó mà suy ra

Với C là giao điểm của đường thẳng EI với đường tròn (C).

Vậy Dấu “=” xảy ra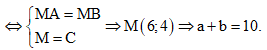

Câu 5:

Cho số phức z = 3 - 2i. Tìm điểm biểu diễn của số phức w = z + i. $\bar{z}$

A. M(1;1)

B. M(1;-5)

C. M(5;-5)

D. M(5;1)

Xem đáp án

Đáp án A

Ta có

Câu 6:

Cho các số phức $z_{1}$ = 1 + 2i, $z_{2}$ = 3 - i. Tìm số phức liên hợp của số phức w = $z_{1}$ + $z_{2}$

A. $\bar{w}$ = -4 + i

B. $\bar{w}$ = 4 + i

C. $\bar{w}$ = -4 - i

D. $\bar{w}$ = 4 - i

Xem đáp án

Đáp án D

Ta có:

Câu 7:

Tìm số phức z thỏa mãn (1-2i)z = 3 + i

A. z = 1 - i

B. z = 1 + i

C. z = $\frac{1}{5} + \frac{7}{5} i$

D. z = $\frac{1}{5} - \frac{7}{5} i$

Xem đáp án

Đáp án C

Ta có

Câu 8:

Tìm môđun của số phức z biết z-4 = (1+i)|z| - (4+3z)i.

A. |z| = 4

B. |z| = 1

C. |z| = $\frac{1}{2}$

D. |z| = 2

Xem đáp án

Đáp án D

Câu 9:

Cho số phức z = 2 + 3i. Gọi M là điểm biểu diễn số phức z, N là điểm biểu diễn số phức $\bar{z}$ và P là điểm biểu diễn số phức (1+i)z. Khẳng định nào sau đây là khẳng định sai?

A. M(2;3)

B. M(2;-3)

C. P(1;5)

D. |z| = $\sqrt{13}$

Xem đáp án

Đáp án C.

Ta có:

Câu 10:

Tìm số phức z thỏa mãn $\bar{z} = \frac{1}{3} [{\bar{(1 - 2 i)}}^{2} - z]$ .

A. - $\frac{3}{4}$ - 2i

B. - $\frac{3}{4}$ + 2i

C. 2 + $\frac{3}{4}$ i

D. 2 - $\frac{3}{4}$ i

Xem đáp án

Đáp án A.

Đặt

Câu 11:

Trên tập $ℂ$ , cho số phức z = $\frac{i + m}{i - 1}$ với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. $\bar{z}$ = 5

A. m = -3

B. m = 1

C. m = $\pm$ 2

D. m = $\pm$ 3

Xem đáp án

Đáp án D.

Ta có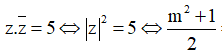

Câu 12:

Cho số phức z thỏa mãn $|\frac{z}{i + 2}|$ = 1. Biết rằng tập các điểm biễu diễn số phức z là một đường tròn (C). Tính bán kính r của đường tròn (C).

A. r = 1

B. r = $\sqrt{5}$

C. r = 2

D. r = $\sqrt{3}$

Xem đáp án

Đáp án B.

Ta có

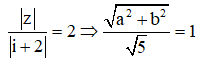
Câu 13:

Cho số phức z thỏa mãn điều kiện 3 $\leq$ |z-3i+1| $\leq$ 5. Tập hợp các điểm biểu diễn của

Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó.

A. S = 25 $π$

B. S = 8 $π$

C. S = 4 $π$

D. S = 16 $π$

Xem đáp án

Đáp án D.

Gọi M là điểm biểu diễn của số phức z. Xét điểm A(-1;3) thì theo điều kiện, ta có

Vậy tập hợp các điểm biểu diễn z là phần hình phẳng nằm giữa 2 đường tròn tâm A, bán kính lần lượt là 3 và 5

$\Rightarrow S = π (5^{2} - 3^{2}) = 16 π$

Câu 14:

Cho số phức z = ${(\sqrt{2} + i)}^{2} . (1 - \sqrt{2} i)$ . Tìm phần thực và ảo của số phức $\bar{z}$ .

A. Phần thực bằng 5 và Phần ảo bằng $\sqrt{2}$ .

B. Phần thực bằng 5 và Phần ảo bằng - $\sqrt{2}$ .

C. Phần thực bằng –5 và Phần ảo bằng $\sqrt{2}$ .

D. Phần thực bằng –5 và Phần ảo bằng - $\sqrt{2}$ .

Xem đáp án

Đáp án B

Vậy phẩn thực và phần ảo của $\bar{z}$ là 5 và $\sqrt{2}$

Câu 15:

Gọi $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $- 3 z^{2}$ + 2z + 1 = 0. Tính P = $\frac{1}{z_{1}} + \frac{1}{z_{2}}$ .

A. P = 9

B. P = 2

C. P = 3

D. P = 10

Xem đáp án

Đáp án B

$z_{1}, z_{2}$ là hai nghiệm phức của phương trình $- 3 z^{2}$ + 2z + 1 = 0 theo Định lý Viét ta có

Câu 16:

Tìm tất cả các số thực x, y sao cho 1 - $x^{2} - y . i = i^{3} - i^{2} - i$ .

A. x = $\sqrt{2}$ , y = 2

B. x = 0, y = 2

C. x = - $\sqrt{2}$ , y = 2

D. x = 2, y = 0

Xem đáp án

Đáp án B

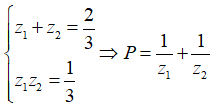
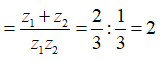
Câu 17:

Cho số phức z thỏa mãn (3+i)z = 13 - 9i. Tìm tọa độ của điểm M biểu diễn z.

A. M = (-3;4)

B. M = (3;-4)

C. M = (-3;-4)

D. M = (1;-3)

Xem đáp án

Đáp án B

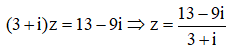
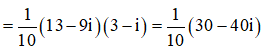
= 3 - 4i

Vậy tọa độ của M(3;-4)

Câu 18:

Cho hai số phức $z_{1}$ = 1 + 2i, $z_{2}$ = 3 - 2i. Tính mô đun của số phức $z_{1}$ - 2 $z_{2}$ .

A. | $z_{1}$ - 2 $z_{2}$ | = $\sqrt{61}$

B. | $z_{1}$ - 2 $z_{2}$ | = $\sqrt{71}$

C. | $z_{1}$ - 2 $z_{2}$ | = $\sqrt{17}$

D. | $z_{1}$ - 2 $z_{2}$ | = 4

Xem đáp án

Đáp án A

Câu 19:

Tính mô đun của số phức z, biết $\bar{z}$ = 1 + 3i.

A. |z| = $\sqrt{5}$

B. |z| = $\sqrt{10}$

C. |z| = 2 $\sqrt{5}$

D. |z| = $2 \sqrt{3}$

Xem đáp án

Đáp án B

Câu 20:

Cho hai số phức $z_{1}$ = 1 - 2i, $z_{2}$ = 3 + i. Tìm phần thực và ảo của số phức z = $z_{1}$ $z_{2}$

A. Phần thực bằng 3 và Phần áo bằng -5i.

B. Phần thực bằng 5 và Phần áo bằng -5i.

C. Phần thực bằng 3 và Phần áo bằng -5.

D. Phần thực bằng 5 và Phần áo bằng -5.

Xem đáp án

Đáp án D

Sử dụng MTBT

Câu 21:

Gọi $z_{1}, z_{2}, z_{3}$ là ba nghiệm phức của phương trình $z^{3}$ - 1 = 0. Tính P = | $z_{1} + z_{2} + z_{3}$ |

A. P = 10

B. P = 13

C. P = 93

D. P = 0

Xem đáp án

Đáp án D

Ta có

Câu 22:

Tìm số phức z thỏa mãn 2iz = -2 + 4i

A. z = 2 + i

B. z = 2 - i

C. z = 1 + 2i

D. z = 1 - 2i

Xem đáp án

Đáp án A

Ta có

Câu 23:

Cho M(1;2) là điểm biểu diễn số phức z. Tìm tọa độ của điểm N biểu diễn số phức w = z + 2 $\bar{z}$ .

A. N = (3;-2)

B. N = (2;-3)

C. N = (2;1)

D. N = (2;3)

Xem đáp án

Đáp án A

Ta có z = 1 + 2i

=> N(3;-2)

Câu 24:

Tìm phần thực và ảo của số phức z = ${(2 + 3 i)}^{2}$

A. Phần thực bằng -5 và Phần ảo bằng 12

B. Phần thực bằng 5 và Phần ảo bằng -12.

C. Phần thực bằng -5 và Phần ảo bằng $\sqrt{12}$

D. Phần thực bằng -5 và Phần ảo bằng - $\sqrt{12}$

Xem đáp án

Đáp án A

Sử dụng máy tính Casio ta có

Câu 25:

Tìm các số thực x, y biết 3x - 2 + (y-5)i = x + 1 - (2y+1)i

$A . x = - \frac{3}{2}; y = - \frac{4}{3}$

$B . x = \frac{2}{3}; y = \frac{3}{4}$

$C . x = - \frac{2}{3}; y = - \frac{3}{4}$

$D . x = \frac{3}{2}; y = \frac{4}{3}$

Xem đáp án

Đáp án D

Ta có

CHỌN BỘ SÁCH BẠN MUỐN XEM

225 Bài tập Số phức ôn thi Đại học có lời giải

225 Bài tập Số phức ôn thi Đại học có lời giải (P5)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm