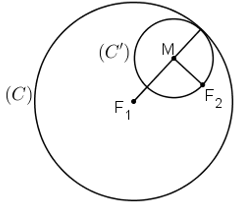
Cho đường tròn (C) tâm F₁ bán kính 2a và một điểm F₂ ở bên trong của (C). Tập hợp tâm M của các đường tròn (C') thay đổi nhưng luôn đi qua F₂ và tiếp xúc với (C)(hình dưới) là đường nào sau đây?

 

Cho hai điểm A(1; 1) và B(7; 5). Phương trình đường tròn đường kính AB là:

Phương trình tiếp tuyến tại M(3 ; 4) với đường tròn (C) : x² + y² – 2x – 4y – 3 = 0 là:

Tính góc giữa hai đường thẳng ∆₁ và ∆₂ trong các trường hợp sau:

a) Δ₁: 2x + y – 4 = 0 và Δ₂ : 5x – 2y + 3 = 0.

b) Δ₁: y = –2x + 4 và Δ₂: 

Cho hai đường thẳng:

$d_1$: 2x+y+4-m=0, $d_2$: (m+3)x+y-2m-1=0

$d_1$ song song với $d_2$ khi:

Phương trình nào sau đây là phương trình đường tròn?

Cho elip (E): 4x2 + 9y2 = 36. Tìm mệnh đề sai trong các mệnh đề sau:

Với giá trị nào của m thì phương trình sau đây là phương trình của đường tròn:

x² + y² – 2(m + 2).x + 4my + 19m – 6 = 0

Bán kính của đường tròn tâm I(0; -2) và tiếp xúc với đường thẳng Δ : 3x – 4y – 23 = 0 là:

Phương trình chính tắc của elip có hai đỉnh là (-3; 0); (3; 0) và hai tiêu điểm là (-1; 0); (1; 0) là:

Cho tam giác ABC có tọa độ các đỉnh là A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao của tam giác vẽ từ A?

Đường thẳng đi qua điểm M(1; 0) và song song với đường thẳng d: 4x + 2y +1 = 0 có phương trình tổng quát là:

Đường tròn (C): x² + y² – x + y – 1 = 0 có tâm I và bán kính R là:

Cho đường tròn (C) x² + y² – 4x – 2y = 0 và đường thẳng Δ: x + 2y + 1 = 0. Tìm mệnh đề đúng trong các mệnh đề sau :

Cho tam giác ABC với các đỉnh là A(-1; 1), B(4; 7) và C(3; -2), M là trung điểm của đoạn thẳng AB. Phương trình tham số của trung tuyến CM là:

Cho điểm M(0; 4) và đường tròn (C) có phương trình x² + y² – 8x – 6y + 21 = 0. Tìm phát biểu đúng trong các phát biểu sau: