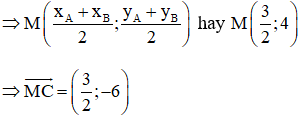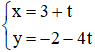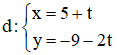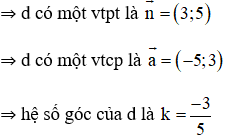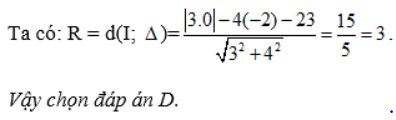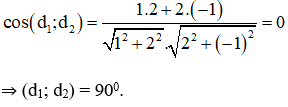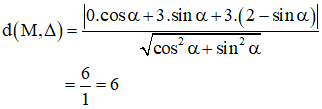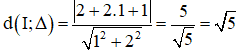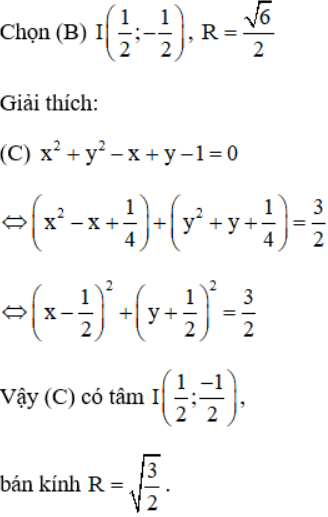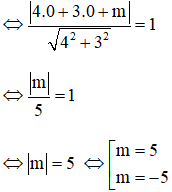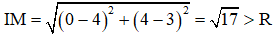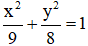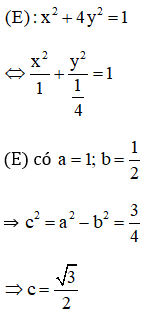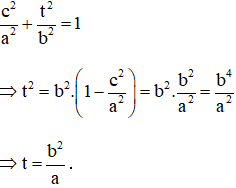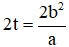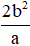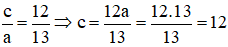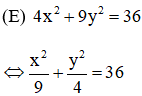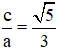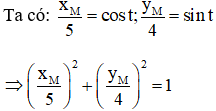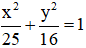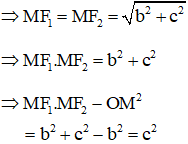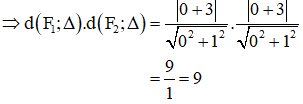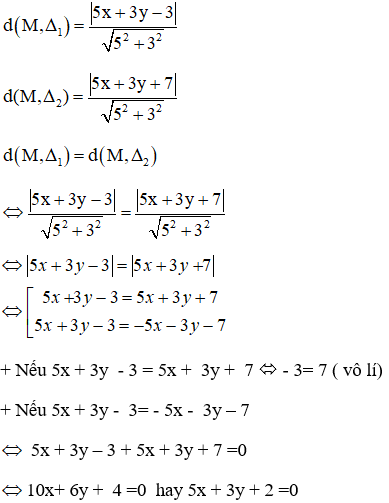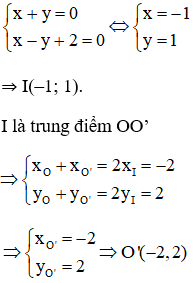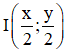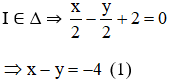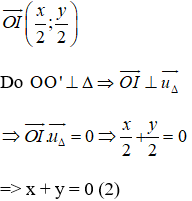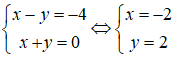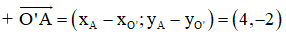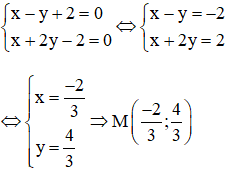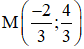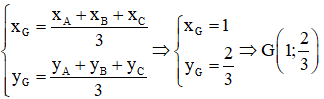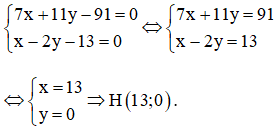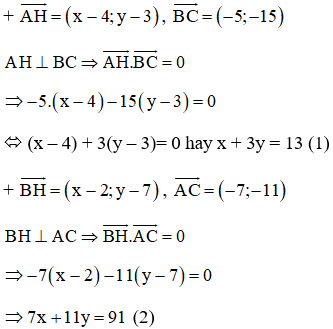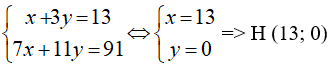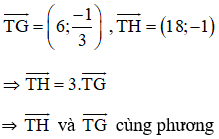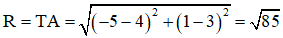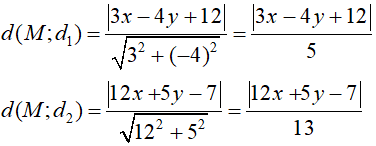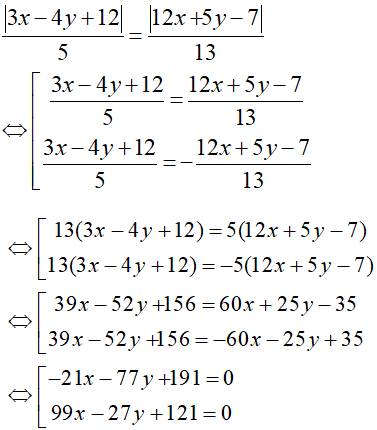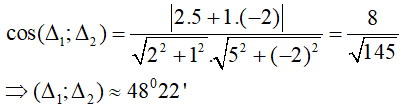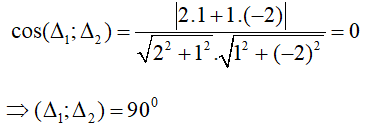Ôn tập chương 3 hình học - Toán 10
-
2212 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có tọa độ các đỉnh là A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao của tam giác vẽ từ A?
 Xem đáp án
Xem đáp án
Chọn A, 2x + 3y – 8 = 0
Giải thích:
Đường cao từ A vuông góc với BC nên nhận 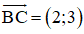
Đường cao đi qua A(1; 2)
⇒ Phương trình đường cao từ A: 2(x - 1) + 3(y – 2) = 0 hay 2x + 3y – 8 = 0.
Câu 2:
Cho tam giác ABC với các đỉnh là A(-1; 1), B(4; 7) và C(3; -2), M là trung điểm của đoạn thẳng AB. Phương trình tham số của trung tuyến CM là:
 Xem đáp án
Xem đáp án
Chọn (B)
Giải thích:
Đường thẳng MC nhận 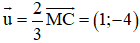
Đường thẳng MC đi qua C(3; –2) nên phương trình đường thẳng MC:
Câu 3:
Cho phương trình tham số của đường thẳng
Trong các phương trình sau, phương trình nào là phương trình tổng quát của đường thẳng (d) ?
 Xem đáp án
Xem đáp án
Chọn (A) 2x + y – 1 = 0
Giải thích :
d nhận 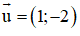
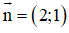
d đi qua A(5 ; –9)
⇒ Phương trình tổng quát của d: 2x + y – 1 = 0.
Câu 4:
Đường thẳng đi qua điểm M(1; 0) và song song với đường thẳng d: 4x + 2y +1 = 0 có phương trình tổng quát là:
 Xem đáp án
Xem đáp án
Chọn (C) 2x + y – 2 = 0.
Giải thích :
Trong các đường thẳng trên, chỉ có đường thẳng 2x + y – 2 = 0 đi qua điểm M(1 ; 0).
Câu 5:
Cho đường thẳng d có phương trình tổng quát: 3x + 5y + 2006 = 0. Tìm mệnh đề sai trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
Chọn (C) (d) có hệ số góc k = 5/3.
Giải thích :
d : 3x + 5y + 2006 = 0
Câu 7:
Cho hai đường thẳng:
: 2x+y+4-m=0, : (m+3)x+y-2m-1=0
song song với khi:
 Xem đáp án
Xem đáp án
Chọn (B) m = –1
Giải thích:
d1: 2x + y + 4 – m = 0;
d2: (m + 3).x + y – 2m – 1 = 0.
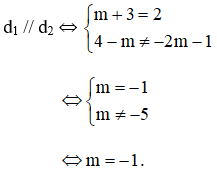
Câu 8:
Cho (d1): x + 2y + 4 = 0 và (d2) : 2x – y + 6 = 0. Số đo của góc giữa hai đường thẳng d1 và d2 là :
 Xem đáp án
Xem đáp án
Chọn (D) 90º
Giải thích :
Góc giữa hai đường thẳng d1 và d2 là :
Câu 9:
Cho hai đường thẳng Δ1: x + y + 5 = 0 và Δ2: y = –10. Góc giữa Δ1 và Δ2 là:
 Xem đáp án
Xem đáp án
Chọn (A) 45º
Giải thích :
Δ1: x + y + 5 = 0
Δ2: y = –10 ⇔ 0.x + y + 10 = 0
Góc giữa Δ1 và Δ2 là:
⇒ (Δ1; Δ2) = 45º.
Câu 10:
Khoảng cách từ điểm M(0; 3) đến đường thường:
 Xem đáp án
Xem đáp án
Chọn (B)
Giải thích:
Khoảng cách từ M đến Δ là:
Câu 11:
Phương trình nào sau đây là phương trình đường tròn?
 Xem đáp án
Xem đáp án
Chọn (D) x2 + y2 – 4x + 6y – 12 = 0.
Giải thích :
+ (A) và (B) không phải phương trình đường tròn vì hệ số của x2 và y2 khác nhau.
+ x2 + y2 – 2x – 8y + 20 = 0
⇔ (x2 – 2x + 1) + (y2 – 8y + 16) + 3 = 0
⇔ (x – 1)2 + (y – 4)2 = –3
–3 < 0 nên x2 + y2 – 2x – 8y + 20 = 0 không phải phương trình đường tròn.
+ x2 + y2 – 4x + 6y – 12 = 0
⇔ (x2 – 4x + 4) + (y2 + 6y + 9) = 25
⇔ (x – 2)2 + (y + 3)2 = 25
Vậy (D) là phương trình đường tròn có tâm là I(2 ; –3) và bán kính bằng 5.
Câu 12:
Cho đường tròn (C) : x2 + y2 + 2x + 4y – 20 = 0. Tìm mệnh đề sai trong các mệnh đề sau :
 Xem đáp án
Xem đáp án
Chọn (A) (C) có tâm I(1 ; 2)
Giải thích:
x2 + y2 + 2x + 4y – 20 = 0
⇔ (x2 + 2x + 1) + (y2 + 4y + 4) = 25
⇔ (x + 1)2 + (y + 2)2 = 25
⇒ (C) có tâm I(–1; –2), bán kính R = 5.
Thay M(2 ; 2) vào phương trình thấy thỏa mãn ⇒ M thuộc (C)
Thay A(1 ; 1) vào phương trình thấy không thỏa mãn ⇒ A không thuộc (C).
Câu 13:
Phương trình tiếp tuyến tại M(3 ; 4) với đường tròn (C) : x2 + y2 – 2x – 4y – 3 = 0 là:
 Xem đáp án
Xem đáp án
Chọn (A) x + y – 7 = 0
Giải thích :
x2 + y2 – 2x – 4y – 3 = 0
⇔ (x2 – 2x + 1) + (y2 – 4y + 4) = 8
⇔ (x – 1)2 + (y – 2)2 = 8
⇒ (C) có tâm I(1; 2)
Gọi d là phương trình tiếp tuyến tại M với (C)
⇒ IM ⊥ d
⇒ d nhận 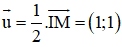
d đi qua M(3 ; 4) ⇒ Phương trình đường thẳng d: x + y – 7 = 0
Câu 14:
Cho đường tròn (C) x2 + y2 – 4x – 2y = 0 và đường thẳng Δ: x + 2y + 1 = 0. Tìm mệnh đề đúng trong các mệnh đề sau :
 Xem đáp án
Xem đáp án
Chọn (C) Δ tiếp xúc với (C) ;
Giải thích :
(C) : x2 + y2 – 4x – 2y = 0
⇔ (x2 – 4x + 4) + (y2 – 2y + 1) = 5
⇔ (x – 2)2 + (y – 1)2 = 5
⇒ (C) có tâm I(2; 1), bán kính R = √5.
Khoảng cách từ tâm I đến đường thẳng Δ bằng:
⇒ d(I; Δ) = R nên đường thẳng Δ tiếp xúc với đường tròn (C).
Câu 16:
Với giá trị nào của m thì phương trình sau đây là phương trình của đường tròn:
x2 + y2 – 2(m + 2).x + 4my + 19m – 6 = 0
 Xem đáp án
Xem đáp án
Chọn (C) m < 1 hoặc m > 2
Giải thích:
x2 + y2 – 2(m + 2).x + 4my + 19m – 6 = 0
⇔ (x2 – 2(m + 2).x + m2 + 4m + 4) + (y2 + 4my + 4m2) = 5m2 – 15m + 10
⇔ (x – m – 2)2 + (y + 2m)2 = 5m2 – 15m + 10
Phương trình trên là phương trình đường tròn
⇔ 5m2 – 15m + 10 > 0
⇔ m < 1 hoặc m > 2
Câu 17:
Đường thẳng Δ: 4x + 3y + m = 0 tiếp xúc với đường tròn (C): x2 + y2 = 1 khi:
 Xem đáp án
Xem đáp án
Chọn (B) m = 5
Giải thích:
(C) x2 + y2 = 1 có tâm O(0; 0) và bán kính R = 1.
Δ tiếp xúc với (C) ⇔ d(I; Δ) = R
Câu 18:
Cho hai điểm A(1; 1) và B(7; 5). Phương trình đường tròn đường kính AB là:
 Xem đáp án
Xem đáp án
Chọn (B) x2 + y2 – 8x – 6y + 12 = 0
Giải thích :
+ Tâm đường tròn là trung điểm I của đoạn thẳng AB
A(1 ; 1) ; B(7 ; 5) ⇒ I(4; 3)
+ Bán kính đường tròn R = AB/2 = √13
⇒ đường tròn đường kính AB là:
(x – 4)2 + (y – 3)2 = 13
⇔ x2 + y2 – 8x – 6y + 12 = 0.
Câu 19:
Đường tròn đi qua ba điểm A(0 ; 2), B(–2 ; 0) và C(2 ; 0) có phương trình là :
 Xem đáp án
Xem đáp án
Chọn (D) x2 + y2 – 4 = 0
Giải thích :
Ta dễ dàng nhận thấy :
xA2 + yA2 = 02 + 22 = 4 ;
xB2 + yB2 = (–2)2 + 02 = 4 ;
xC2 + yC2 = 22 + 02 = 4
Do đó A, B, C đều thuộc đường tròn x2 + y2 = 4.
Câu 20:
Cho điểm M(0; 4) và đường tròn (C) có phương trình x2 + y2 – 8x – 6y + 21 = 0. Tìm phát biểu đúng trong các phát biểu sau:
 Xem đáp án
Xem đáp án
Chọn (A) M nằm ngoài (C)
Giải thích:
(C) x2 + y2 – 8x – 6y + 21 = 0
⇔ (x2 – 8x + 16) + (y2 – 6y + 9) = 4
⇔ (x – 4)2 + (y – 3)2 = 4
⇒ (C) có tâm I(4; 3) và bán kính R = 2
Ta có :
Do đó M nằm ngoài đường tròn (C).
Câu 21:
Cho elip (E): 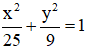
(I) (E) có các tiêu điểm F1(–4 ; 0) và F2(4 ; 0) ;
(II) (E) có các tỉ số 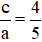
(III) (E) có đỉnh A1(–5 ; 0) ;
(IV) (E) có độ dài trục nhỏ bằng 3.
Tìm mệnh đề sai trong các mệnh đề trên:
 Xem đáp án
Xem đáp án
- Chọn đáp án
- Giải thích:
(E): 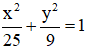
+ Các tiêu điểm của (E) là F1(–4; 0) và F2(4; 0) nên (I) đúng.
+ 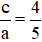
+ Các đỉnh của (E): A1(–5 ; 0); A2(5; 0); B1(0; -3); B2(0; 3) nên (III) đúng
+ Độ dài trục nhỏ bằng 2b = 6 nên (IV) sai.
Câu 22:
Phương trình chính tắc của elip có hai đỉnh là (-3; 0); (3; 0) và hai tiêu điểm là (-1; 0); (1; 0) là:
 Xem đáp án
Xem đáp án
Chọn (C)
Giải thích :
(E) có hai đỉnh A1(-3; 0) và A2(3; 0) nên a = 3
(E) có hai tiêu điểm F1(-1; 0) và F2(1; 0) nên c = 1
⇒ b2 = a2 – c2 = 8
Vậy phương trình chính tắc của (E) là:
Câu 23:
Cho elip (E) : x2 + 4y2 = 1 và cho các mệnh đề:
(I) (E) có trục lớn bằng 1;
(II) (E) có trục nhỏ bằng 4;
(III) (E) có tiêu điểm 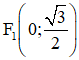
(IV) (E) có tiêu cự bằng √3.
Tìm mệnh đề đúng trong các mệnh đề trên:
 Xem đáp án
Xem đáp án
Chọn (D) (IV)
Giải thích:
+ độ dài trục lớn bằng 2a = 2 nên (I) sai
+ độ dài trục nhỏ bằng 2b = 1 nên (II) sai
+ Hai tiêu điểm là 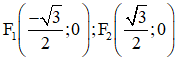
+ Tiêu cự bằng 2c = √3 nên (IV) đúng.
Câu 24:
Dây cung của elip (E) : 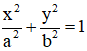
 Xem đáp án
Xem đáp án
Chọn (B)
Giải thích :
Gọi dây cung đó là CD vuông góc với trục lớn tại tiêu điểm F2(c ; 0) nên C, D có hoành độ đều bằng c
⇒ C(c; t) ; D(c; -t)
C, D nằm trên Elip nên ta có :
Độ dài đoạn thẳng CD bằng
Vậy độ dài dây cung cần tìm của (E) là
Câu 25:
Một elip có trục lớn bằng 26, tỉ số 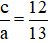
 Xem đáp án
Xem đáp án
Chọn (B) 10
Giải thích :
+ Độ dài trục lớn bằng 26 ⇒ 2a = 26 ⇒ a = 13
+ Tỉ số
⇒ b2 = a2 – c2 = 132 – 122 = 25 ⇒ b = 5
⇒ Độ dài trục nhỏ bằng 2b = 10.
Câu 26:
Cho elip (E): 4x2 + 9y2 = 36. Tìm mệnh đề sai trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
Chọn (C) (E) có tiêu cự bằng √5.
Giải thích:
⇒ (E) có a = 3; b = 2 ⇒ c2 = a2 – b2 = 5 ⇒ c = √5
+ (E) có trục lớn bằng 2a = 6, trục nhỏ bằng 2b = 4, tiêu cự bằng 2c = 2√5, tỉ số
Câu 27:
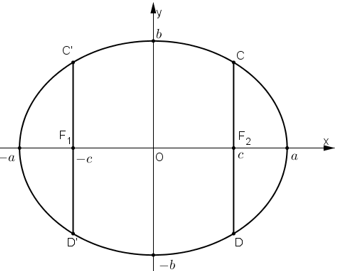
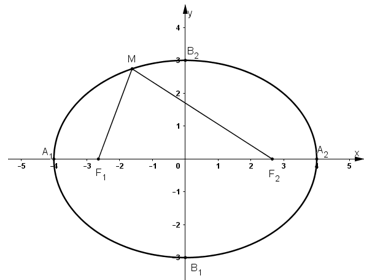
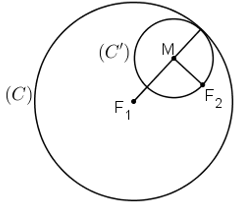
Cho đường tròn (C) tâm F1 bán kính 2a và một điểm F2 ở bên trong của (C). Tập hợp tâm M của các đường tròn (C') thay đổi nhưng luôn đi qua F2 và tiếp xúc với (C)(hình dưới) là đường nào sau đây?
 Xem đáp án
Xem đáp án
Chọn (C) Elip
Giải thích:
Đường tròn tâm M, bán kính R tiếp xúc trong với đường tròn (F1; 2a) nên ta có:
R + F1M = 2a
Đường tròn tâm M, bán kính R đi qua F2 nên R = MF2
Do đó ta có: MF1 + MF2 = 2a = const
Do đó M thuộc elip có hai tiêu điểm F1; F2 và độ dài trục lớn bằng 2a.
Câu 28:
Khi cho t thay đổi, điểm M(5cost; 4sint) di động trên đường nào sau đây?
 Xem đáp án
Xem đáp án
Chọn (A) Elip
Giải thích:
⇒ Với t thay đổi, M luôn thuộc đường elip:
Câu 29:
Cho elip (E): 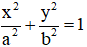
 Xem đáp án
Xem đáp án
Chọn (A)
Giải thích:
F1; F2 là hai tiêu điểm của elip nên F1(-c; 0) và F2(c; 0)
Câu 30:
Cho elip (E): và đường thẳng Δ: y + 3 = 0. Tích các khoảng cách từ hai tiêu điểm của (E) đến đường thẳng Δ bằng giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Chọn (B) 9
Giải thích:
(E): có a2 = 16; b2 = 9 ⇒ c2 = a2 – b2 = 7 ⇒ c = √7.
⇒ Hai tiêu điểm của (E) là F1(-√7 ; 0) và F2(√7 ; 0)
Câu 31:
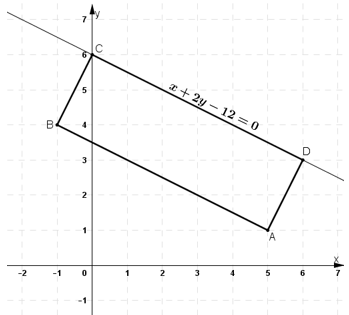
Cho hình chữ nhật ABCD. Biết các đỉnh A(5; 1), C(0; 6) và phương trình CD: x + 2y -12 = 0. Tìm phương trình đường thẳng chứa các cạnh còn lại.
 Xem đáp án
Xem đáp án
CD: x + 2y – 12 = 0 ⇒ CD nhận 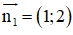
⇒ CD nhận 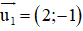
+ ABCD là hcn ⇒ AD ⊥ CD ⇒ AD nhận 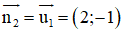
A(5 ; 1) ∈ AD
⇒ Phương trình đường thẳng AD: 2( x- 5) – 1(y – 1) = 0 hay 2x – y – 9 = 0.
+ ABCD là hcn ⇒ AB // CD ⇒ AB nhận 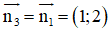
A(5;1) ∈ AB
⇒ Phương trình đường thẳng AB: 1( x- 5) + 2(y -1) = 0 hay x + 2y – 7 = 0
+ ABCD là hcn ⇒ BC ⊥ CD ⇒ BC nhận 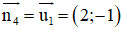
C(0, 6) ∈ CD
⇒ Phương trình đường thẳng BC: 2(x- 0)- 1(y – 6) =0 hay 2x – y + 6 = 0.
Câu 32:
Cho A(1; 2), B(-3; 1) và C(4; -2). Tìm tập hợp các điểm M sao cho MA2 + MB2= MC2
 Xem đáp án
Xem đáp án
Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.
Câu 33:
Tìm tập hợp các điểm cách đều hai đường thẳng: (Δ1): 5x + 3y – 3 = 0 và (Δ2) : 5x + 3y + 7 = 0.
 Xem đáp án
Xem đáp án
Gọi điểm cách đều hai đường thẳng (Δ1) và (Δ2) là M(x, y).
Ta có:
Vậy tập hợp các điểm M cách đều hai đường thẳng đã cho là
đường thẳng: 5x + 3y + 2 = 0.
Câu 34:
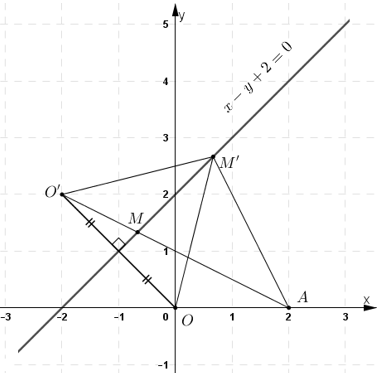
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0).
a, Tìm điểm đối xứng của O qua Δ.
b, Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
 Xem đáp án
Xem đáp án
a, Cách 1: Gọi O’ là điểm đối xứng với O qua (Δ)
⇒ OO’ ⊥ Δ tại trung điểm I của OO’.
+ (Δ) nhận 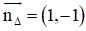
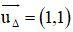
OO’ ⊥ Δ ⇒ OO’ nhận 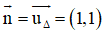
⇒ Phương trình đường thẳng OO’: x + y = 0.
+ I là giao OO’ và Δ nên tọa độ của I là nghiệm của hệ phương trình:
Cách 2: Gọi O’(x, y) là điểm đối xứng với O qua Δ.
+ Trung điểm I của OO’ là
+ (Δ) nhận 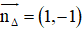
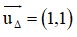
Từ (1) và (2) ta có hệ phương trình
Vậy O’(–2; 2).
b)
+ Vì O và A nằm cùng một nửa mặt phẳng
bờ là đường thẳng Δ nên đoạn thẳng OA không cắt Δ.
O’ và A thuộc hai nửa mặt phẳng khác nhau
bờ là đường thẳng Δ nên O’A cắt Δ.
Do O’ đối xứng với O qua đường thẳng ∆ nên
∆ là đường trung trực của đoạn thẳng OO’,
với mọi M ∈ Δ ta có MO = MO’.
Độ dài đường gấp khúc OMA bằng OM + MA = O’M + MA ≥ O’A.
⇒ O’M + MA ngắn nhất khi O’M + MA = O’A
⇔ M là giao điểm của O’A và Δ.
⇒ O’A nhận 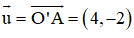
⇒ O’A nhận 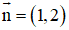
⇒ Phương trình đường thẳng
O’A : 1(x - 2) + 2(y - 0)= 0 hay x + 2y – 2 = 0.
M là giao điểm của O’A và Δ nên tọa độ điểm M là nghiệm của hệ :
Vậy điểm M cần tìm là
Câu 35:
Cho ba điểm A(4; 3), B(2; 7) và C(-3; -8).
a, Tìm tọa độ trọng tâm G và trực tâm H của tam giác ABC;
b, Gọi T là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh T, G và H thẳng hàng.
c, Viết phương trình đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
a)
– Tọa độ trọng tâm G của tam giác ABC là:
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận 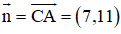
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng
BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận 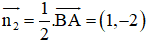
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng
CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE
nên tọa độ của H là nghiệm của hpt:
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
Từ (1) và (2) ta có hệ phương trình
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
Vậy phương trình đường tròn ngoại tiếp tam giác ABC :
(x + 5)2 + (y – 1)2 = 85
Câu 36:
Lập phương trình hai đường phân giác của các góc tạo bởi hai đường thẳng 3x – 4y + 12 = 0 và 12x + 5y – 7 = 0.
 Xem đáp án
Xem đáp án
Gọi M(x;y) là điểm thuộc đường phân giác của góc tạo bởi hai đường thẳng đã cho
+) Ta có:
+) Do điểm M thuộc đường phân giác của góc tạo bởi hai đường thẳng d1 và d2 nên điểm M cách đều hai đường thẳng trên: d( M; d1)= d(M, d2 )
Vậy phương trình 2 đường phân giác của góc tạo bởi hai đường thẳng đã cho là:
-21 x – 77y + 191= 0 và 99x – 27y + 121 =0
Câu 37:
Cho đường tròn (C) có tâm I(1; 2) và bán kính bằng 3. Chứng minh rằng tập hợp các điểm M mà từ đó vẽ được hai tiếp tuyến với (C) tạo với nhau một góc 60o là một đường tròn. Hãy viết phương trình đường tròn đó.
 Xem đáp án
Xem đáp án
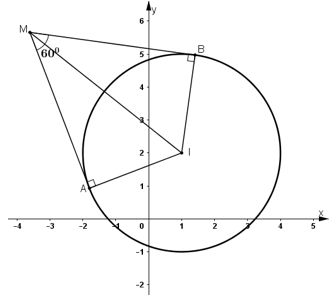
Gọi A, B là hai tiếp điểm của tiếp tuyến kẻ từ M đến (C).
Mà điểm I là cố định nên tập hợp các điểm M là đường tròn tâm I,
bán kính R = 6 và có phương trình: (x – 1)2 + (y – 2)2 = 36.
Câu 38:
Tính góc giữa hai đường thẳng ∆1 và ∆2 trong các trường hợp sau:
a) Δ1: 2x + y – 4 = 0 và Δ2 : 5x – 2y + 3 = 0.
b) Δ1: y = –2x + 4 và Δ2:
 Xem đáp án
Xem đáp án
a) Hai đường thẳng Δ1 và Δ2 có
vecto pháp tuyến lần lượt là: n1→(2;1); n2→(5;-2)
Góc giữa hai đường thẳng (Δ1) và (Δ2) là:
b) Cách 1:
Δ1: y = –2x + 4 ⇔ 2x + y – 4 = 0
Δ2: 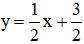
Hai đường thẳng Δ1 và Δ2 có
vecto pháp tuyến lần lượt là: n1→(2;1); n2→(1;-2)
Góc giữa (Δ1) và (Δ2):
Cách 2:
Δ1: y = –2x + 4 có hệ số góc k1 = –2
Δ2: 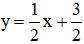
Nhận thấy k1.k2 = –1 nên Δ1 ⊥ Δ2 ⇒ (Δ1, Δ2) = 90°.
Câu 39:
Cho elip (E): 
 Xem đáp án
Xem đáp án
Elip (E): 
+ Các đỉnh của elip là: A1(–4; 0); A2(4; 0); B1(0; –3); B2(0; 3).
+ Tiêu điểm của elip: F1(–√7; 0); F2(√7; 0).
+ Vẽ elip:
Câu 40:
Ta biết rằng Mặt Trăng chuyển động quang Trái Đất theo một quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có chiều dài trục lớn và trục nhỏ lần lượt là 769 266 km và 768 106 km. Tính khoảng cách ngắn nhất và khoảng cách dài nhất từ Trái Đất đến Mặt Trăng, biết rằng các khoảng cách đó đạt được khi Trái Đất và Mặt Trăng nằm trên trục lớn của elip
 Xem đáp án
Xem đáp án
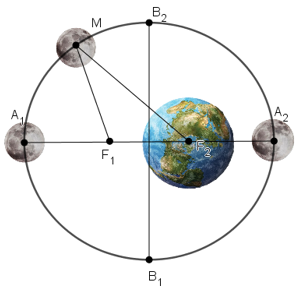
Theo đề bài có:
Độ dài trục lớn của elip bằng 769266km
⇒ A1A2 = 2a = 769266 ⇒ a = 384633
Độ dài trục nhỏ của elip bằng 768106km
⇒ B1B2 = 2b = 768106 ⇒ b = 384053
⇒ c2 = a2 – b2 = 445837880 ⇒ c ≈ 21115
⇒ F1F2 = 2c = 42230
⇒ A1F1 = A2F2 = (A1A2 – F1F2)/2 = 363518
+ Trái Đất gần Mặt Trăng nhất khi Mặt Trăng ở điểm A2
⇒ khoảng cách ngắn nhất giữa Trái Đất và Mặt Trăng bằng A2F2 = 363518 km
+ Trái Đất xa Mặt Trăng nhất khi Mặt Trăng ở điểm A1
⇒ khoảng cách xa nhất giữa Trái Đất và Mặt Trăng bằng:
A1F2 = A1F1 + F1F2 = 405748 km.