Cho ba điểm A(4; 3), B(2; 7) và C(-3; -8).
a, Tìm tọa độ trọng tâm G và trực tâm H của tam giác ABC;
b, Gọi T là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh T, G và H thẳng hàng.
c, Viết phương trình đường tròn ngoại tiếp tam giác ABC.
 Giải bởi Vietjack
Giải bởi Vietjack
a)
– Tọa độ trọng tâm G của tam giác ABC là:
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận 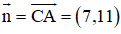
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng
BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận 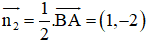
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng
CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE
nên tọa độ của H là nghiệm của hpt:
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
Từ (1) và (2) ta có hệ phương trình
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
Vậy phương trình đường tròn ngoại tiếp tam giác ABC :
(x + 5)2 + (y – 1)2 = 85
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hai điểm A(1; 1) và B(7; 5). Phương trình đường tròn đường kính AB là:
Phương trình tiếp tuyến tại M(3 ; 4) với đường tròn (C) : x2 + y2 – 2x – 4y – 3 = 0 là:
Tính góc giữa hai đường thẳng ∆1 và ∆2 trong các trường hợp sau:
a) Δ1: 2x + y – 4 = 0 và Δ2 : 5x – 2y + 3 = 0.
b) Δ1: y = –2x + 4 và Δ2:
Cho hai đường thẳng:
: 2x+y+4-m=0, : (m+3)x+y-2m-1=0
song song với khi:
Cho elip (E): 4x2 + 9y2 = 36. Tìm mệnh đề sai trong các mệnh đề sau:
Với giá trị nào của m thì phương trình sau đây là phương trình của đường tròn:
x2 + y2 – 2(m + 2).x + 4my + 19m – 6 = 0
Bán kính của đường tròn tâm I(0; -2) và tiếp xúc với đường thẳng Δ : 3x – 4y – 23 = 0 là:
Phương trình chính tắc của elip có hai đỉnh là (-3; 0); (3; 0) và hai tiêu điểm là (-1; 0); (1; 0) là:
Cho tam giác ABC có tọa độ các đỉnh là A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao của tam giác vẽ từ A?
Đường thẳng đi qua điểm M(1; 0) và song song với đường thẳng d: 4x + 2y +1 = 0 có phương trình tổng quát là:
Đường tròn (C): x2 + y2 – x + y – 1 = 0 có tâm I và bán kính R là:
Cho đường tròn (C) x2 + y2 – 4x – 2y = 0 và đường thẳng Δ: x + 2y + 1 = 0. Tìm mệnh đề đúng trong các mệnh đề sau :
Đường tròn đi qua ba điểm A(0 ; 2), B(–2 ; 0) và C(2 ; 0) có phương trình là :
Cho điểm M(0; 4) và đường tròn (C) có phương trình x2 + y2 – 8x – 6y + 21 = 0. Tìm phát biểu đúng trong các phát biểu sau: