Cho hàm số y=f(x) có đạo hàm \[f\prime (x) = (x - 1)({x^2} - 2)({x^4} - 4)\] Số điểm cực trị của hàm số y=f(x) là:
A.3
B.2
C.4
D.1
Giải bởi Vietjack
Ta có: \[f'\left( x \right) = 0\]
\[\begin{array}{l} \Leftrightarrow (x - 1)({x^2} - 2)({x^4} - 4) = 0\\ \Leftrightarrow (x - 1){({x^2} - 2)^2}({x^2} + 2) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = \sqrt 2 }\\{x = - \sqrt 2 }\end{array}} \right.\end{array}\]Một điểm được gọi là cực trị của hàm số khi đạo hàm của hàm số đổi dấu qua điểm đó.
Ta nhận thấy đạo hàm của hàm số chỉ đổi dấu qua x=1 và không đổi dấu qua \[x = \pm \sqrt 2 \]
Vậy hàm số có 1 điểm cực trị.
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Điều kiện để hàm số bậc ba không có cực trị là phương trình y′=0 có:
Cho hàm số \[y = f\left( x \right)\;\]có đạo hàm \[f\prime \left( x \right) = {x^2}({x^2} - 1).\] Điểm cực tiểu của hàm số \[y = f\left( x \right)\;\] là:
Hình vẽ dưới đây mô tả số người nhiễm Covid-19 đang được điều trị ở Việt Nam tính từ ngày 23/01/2020 đến ngày 13/02/2021.
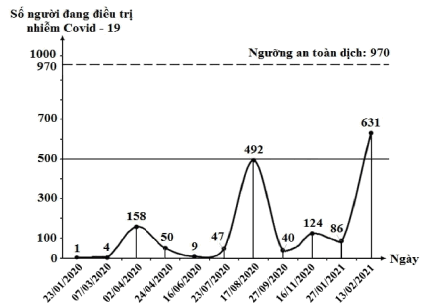
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người được điều trị Covid-19 nhiều nhất?
Cho các phát biểu sau:
1. Hàm số y=f(x) đạt cực đại tại \[{x_0}\] khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua \[{x_0}\].
2. Hàm số y=f(x) đạt cực trị tại \[{x_0}\] khi và chỉ khi \[{x_0}\] là nghiệm của đạo hàm.
3. Nếu \[f\prime (x0) = 0\;\] và \[f\prime \prime (x0) = 0\;\] thì \[{x_0}\] không phải là cực trị của hàm số y=f(x) đã cho.
4. Nếu f′(x0)=0 và \[f\prime \prime (xo) > 0\;\] thì hàm số đạt cực đại tại \[{x_0}\].
Các phát biểu đúng là:
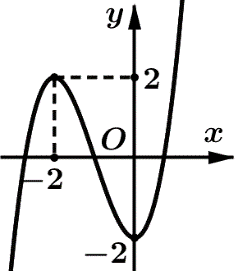
Cho hàm số \[f\left( x \right) = a{x^3} + b{x^2} + cx + d\] (với \[a,b,c,d \in \mathbb{R}\;\] và \[a \ne 0\]) có đồ thị như hình vẽ. Số điểm cực trị của hàm số \[g(x) = f( - 2{x^2} + 4x)\;\] là
Cho hàm số y=f(x) có bảng biến thiên như sau:
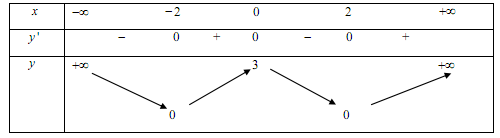
Khẳng định nào sau đây là khẳng định sai:
Cho hàm số y=f(x) có đạo hàm trên (a;b). Nếu \[f\prime (x)\;\] đổi dấu từ âm sang dương qua điểm \[{x_0}\] thuộc (a;b) thì
Số điểm cực trị của đồ thị hàm số \[y = \frac{{x - 1}}{{2 - x}}\] là:
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số \[y = {x^3} - 3{x^2} + 1\] là:
Cho hàm số f(x) có đạo hàm \[f\prime (x) = x(x - 1){(x + 4)^3},\forall x \in \mathbb{R}.\] Số điểm cực tiểu của hàm số đã cho là:
Cho hàm số \[y = \frac{{ - {x^2} + 3x + 6}}{{x + 2}}\], chọn kết luận đúng:
Giả sử \[y = f(x)\;\] có đạo hàm cấp hai trên (a;b). Nếu \(\left\{ {\begin{array}{*{20}{c}}{f'\left( {{x_0}} \right) = 0}\\{f''\left( {{x_0}} \right) > 0}\end{array}} \right.\) thì
