Cho hai số thực dương $a >1,\,\,b >1$ và biết phương trình ${a^{{x^2}}}{b^{x + 4}} = 1$ có nghiệm thực. Giá trị nhỏ nhất của biểu thức $P = {\log _a}\left( {\frac{b}{{{a^3}}}} \right) + \frac{{16}}{{{{\log }_a}b}}$ nằm trong khoảng nào?

Tập xác định của hàm số $y = {\log _3}\left( {x - 1} \right)$ là

Trong mặt phẳng cho 40 điểm tạo thành đa giác đều. Lấy ngẫu nhiên 4 điểm, tính xác suất sao cho 4 điểm này tạo thành hình chữ nhật mà không phải là hình vuông.

Lớp 12A có 18 học sinh nữ và 17 học sinh nam. Giáo viên Chọn đáp án 1 học sinh trong lớp làm tình nguyện viên tham gia phong trào thanh niên của nhà trường. Hỏi có bao nhiêu cách chọn

Thể tích khối chóp có đường cao bằng $a$ và diện tích đáy bằng $2{a^2}\sqrt 3$ là

Phương trình ${4^x} - {3.2^x} + 2 = 0$ có nghiệm thuộc khoảng

Đạo hàm của hàm số $y = {7^x}$ trên $\mathbb{R}$ là

Cho cấp số nhân

$\left( {{u_n}} \right)$ với ${u_1} = \,3$ và ${u_2} = 12$. Công bội của cấp số nhân đã cho bằng

Cho tứ diện đều $ABCD$ .Cosin của góc giữa hai mặt phẳng $\left( {ABC} \right)$ và $\left( {DBC} \right)$ bằng

Gọi $S$ là tập hợp các giá trị nguyên của $m$ để hàm số $f\left( x \right) = - 9{x^3} + 9\left( {m + 1} \right){x^2} - 3\left( {2m + 5} \right)x + \frac{{22}}{7}$ nghịch biến trên $\mathbb{R}$. Tìm số phần tử của tập $S$.

Cho hình trụ có chiều cao $8a$. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song song với trục và cách trục một khoảng bằng $2a$ thì thiết diện thu được là một hình chữ nhật có diện tích bằng $48{a^2}$. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng

Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$. Góc giữa $CA'$ và mặt $(AA'B'B)$ bằng $30^\circ$. Gọi $I$ là trung điểm $AB$. Tính khoảng cách giữa $A'I$ và $AC$

Cho $a$ và $b$ là hai số thực dương, biết rằng ${\log _3}\left( {ab} \right) = {\log _{81}}\left( {\frac{b}{a}} \right)$. Mệnh đề nào dưới đây đúng ?

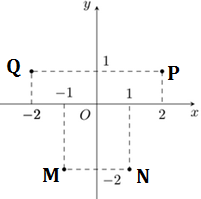
Cho số phức $z$ thỏa mãn điều kiện $z - \left( {2 + 3i} \right)\bar z = 1 - 9i$. Số phức $w = \frac{5}{{iz}}$ có điểm biểu diễn là điểm nào trong các điểm $M$, $N$, $P$, $Q$ ở hình sau ?

Cho hai số phức ${z_1} = 1 - 2i$ và ${z_2} = 5 + i$. Điểm biểu diễn của số phức ${z_1} - {z_2}$ là