Cho hai số phức \[{z_1}\], \[{z_2}\] thỏa mãn \[\left| {{z_1} + 2 - 3i} \right| = 2\] và \[\left| {\overline {{z_2}} - 1 - 2i} \right| = 1\]. Tìm giá trị lớn nhất của \[\left| {{z_1} - {z_2}} \right|\].
A.\[3 + \sqrt {34} .\]
B.\[3 + \sqrt {10} .\]
C.\[6.\]
D.\[3.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án B
Ta có \({\left[ {f'\left( x \right)} \right]^3} + {x^2}.f'\left( x \right) = 2{x^3} + 4{x^2} + 3x + 1 = {\left( {x + 1} \right)^3} + {x^2}\left( {x + 1} \right)\)
\( \Rightarrow {\left[ {f'\left( x \right)} \right]^3} - {\left( {x + 1} \right)^3} + {x^2}\left[ {f'\left( x \right) - x - 1} \right] = 0\)
\( \Rightarrow \left[ {f'\left( x \right) - x - 1} \right].\left[ {{{\left( {f'\left( x \right)} \right)}^2} + \left( {x + 1} \right).f'\left( x \right).{{\left( {x + 1} \right)}^2} + {x^2}} \right] = 0\)(1)
Lại có \({\left( {f'\left( x \right)} \right)^2} + \left( {x + 1} \right).f'\left( x \right).{\left( {x + 1} \right)^2} + {x^2} = {\left[ {f'\left( x \right) + \frac{{x + 1}}{2}} \right]^2} + \frac{3}{4}{\left( {x + 1} \right)^2} + {x^2} \ge 0,\forall x \in \mathbb{R}.\)
Dấu “=” xảy ra \( \Leftrightarrow {\left[ {f'\left( x \right) + \frac{{x + 1}}{2}} \right]^2} = \frac{3}{4}{\left( {x + 1} \right)^2} = {x^2} = 0.\)
Đây là điều kiện vô lý nên dấu “=” không xảy ra \( \Rightarrow {\left[ {f'\left( x \right) + \frac{{x + 1}}{2}} \right]^2} + \frac{3}{4}{\left( {x + 1} \right)^2} + {x^2} >0,\forall x \in \mathbb{R}\)
Do đó (1) \( \Leftrightarrow f'\left( x \right) = x + 1 \Rightarrow f\left( x \right) = \int {\left( {x + 1} \right)dx} = \frac{{{x^2}}}{2} + x + C.\)
Mà \[f\left( 0 \right) = 2 \Rightarrow C = 2 \Rightarrow f\left( x \right) = \frac{{{x^2}}}{2} + x + 2 \Rightarrow \int\limits_0^6 {f\left( x \right)dx} = \left. {\left( {\frac{{{x^3}}}{6} + \frac{{{x^2}}}{2} + 2x} \right)} \right|_0^6 = 66.\]
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz,cho đường thẳng \[d:\frac{{x - 2}}{2} = \frac{{y + 3}}{1} = \frac{{z - 1}}{{ - 2}}.\] Vectơ nào dưới đây là một vectơ chỉ phương của d?
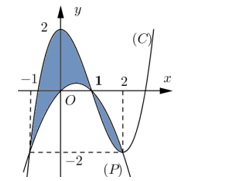
Hình phẳng \[\left( H \right)\] được giới hạn bởi đồ thị (C) của hàm số đa thức bậc ba và parabol \[\left( P \right)\] có trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng
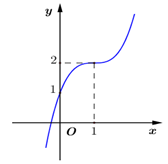
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
Cho phương trình phức \[{z^2} - bz + c = 0\] (\[b,{\rm{ }}c \in \mathbb{R}\]) có một nghiệm \[z = 3 + i.\] Tính \[b + c.\]
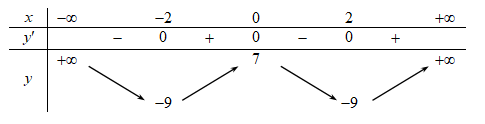
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn số phức z thỏa mãn \[\left| {z - 1 + 4i} \right| = 2.\]
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \[\left( P \right):2x - 5y - z = 0\] và đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y + 1}}{1} = \frac{{z - 3}}{{ - 1}}.\] Viết phương trình đường thẳng Δ vuông góc mặt phẳng (P) tại giao điểm của đường thẳng dvà mặt phẳng (P).
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] và có đồ thị (C) như hình vẽ. Diện tích S của hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 1,{\rm{ }}x = 2\] được tính theo công thức?
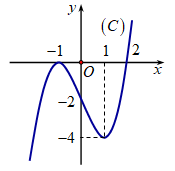
Tính đạo hàm của hàm số \[y = \ln \left( {1 + \sqrt {2x + 1} } \right).\]
Trong không gian Oxyz,cho mặt phẳng \[\left( P \right):x - 6y + 12 = 0.\] Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Tích phân \[\int\limits_0^{\frac{\pi }{{12}}} {\sin 3xdx} \] bằng
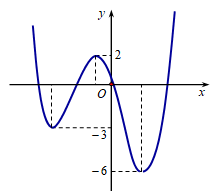
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số \[y = \left| {f\left( {x - 2020} \right) + m} \right|\] có đúng 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
Giải phương trình \[{\log _2}\left( {x + 12} \right).{\log _x}2 = 2.\]
Cho hình thang \[ABCD\] có \[\widehat {BAD} = \widehat {ADC} = 90^\circ \] và \[AB = 8,{\rm{ }}CD = BC = 5.\] Tính thể tích V của khối tròn xoay, nhận được khi quay hình thang \[ABCD\] xung quanh trục \[AB.\]