Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường vuông góc chung của hai đường chéo nhau \({d_1}\) và \({d_2}\) biết \({d_1}:\frac{{x - 2}}{1} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 2}}{{ - 1}}\) và \({d_2}:\left\{ \begin{array}{l}x = t\\y = 3\\z = - 2 + t\end{array} \right.\).
A. \(\left\{ \begin{array}{l}x = 2 + t\\y = 1 + 2t\\z = 2 - t\end{array} \right..\)
B. \(\left\{ \begin{array}{l}x = - 3 - t\\y = - 3 - 2t\\z = - 1 + t\end{array} \right..\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Gọi \(\Delta \) là đường vuông góc chung của \({d_1}\) và \({d_2}\)
Vectơ chỉ phương của đường thẳng \({d_1}\) và \({d_2}\) lần lượt là \(\overrightarrow {{u_1}} \left( {1; - 1; - 1} \right)\) và \(\overrightarrow {{u_2}} \left( {1;0;1} \right).\)
Suy ra \(\overrightarrow {{u_\Delta }} = \left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right] = \left( { - 1; - 2;1} \right)\)
Gọi \(A\left( {2 + t;1 - t;2 - t} \right) \in {d_1}\) và \(B\left( {u;3; - 2 + u} \right) \in {d_2}\) suy ra \(\overrightarrow {AB} \left( {u - t - 2;2 + t;u + t - 4} \right)\)
Giải: \(\overrightarrow {AB} = k.\overrightarrow {{u_\Delta }} = k\left( { - 1; - 2;1} \right) \Leftrightarrow \left\{ \begin{array}{l}u - t - 2 = - k\\2 + t = - 2k\\u + t - 4 = k\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u = 3\\t = 0\\k = - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A\left( {2;1;2} \right)\\B\left( {3;3;1} \right)\end{array} \right..\)
Phương trình đường thẳng AB là \(\left\{ \begin{array}{l}x = 2 + t\\y = 1 + 2t\\z = 2 - t\end{array} \right..\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với \(AB = 2a,AD = 3a.\) Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD, tính khoảng cách giữa BE và SA
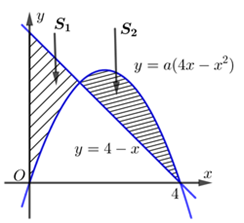
Cho đường thẳng \(y = 4 - x\) và Parabol \(y = a\left( {4x - {x^2}} \right)\) (a là tham số thực dương). Gọi \({S_1}\) và \({S_2}\) lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi \({S_1} = {S_2}\) thì a thuộc khoảng nào sau đây
Trong không gian với hệ tọa độ Oxyz, điều kiện cần và đủ để phương trình \({x^2} + {y^2} + {z^2} + 2x + 4y - 6z + {m^2} - 9m + 4 = 0\) là phương trình mặt cầu.
Giả sử \({z_1},{z_2}\) là hai trong các số phức z thỏa mãn \(\left( {z - 6} \right)\left( {8 + \overline {zi} } \right)\) là số thực. Biết rằng \(\left| {{z_1} - {z_2}} \right| = 4.\) Tập hợp điểm biểu diễn số phức \[w = {z_1} + {z_2}\] là một đường tròn có bán kính bằng
Cho biểu thức \(P = \sqrt[3]{{x.\sqrt[4]{{{x^3}\sqrt x }}}},\) với \(x > 0.\) Mệnh đề nào dưới đây đúng?
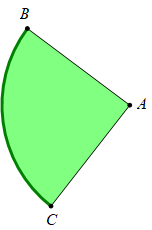
Một mảnh giấy hình quạt như hình vẽ có bán kính \(AB = AC = 8\,\,cm.\) Người ta dán mép AB và AC lại với nhau để được một hình nón đỉnh A. Biết độ dài cung BC bằng \(8\pi \sqrt 3 \,\,cm,\) tính thể tích V của khối nón thu được (xem phần giấy dán không đáng kể)
Cho khối nón có bán kính đáy \(r = \sqrt 3 \) và chiều cao \(h = 4.\) Tính thể tích V của khối nón đã cho
Giải bóng chuyền VTV Cup gồm 12 đội bóng tham dự, trong đó có 9 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C mỗi bảng 4 đội. Tính xác suất để 3 đội bóng của Việt Nam ở ba bảng khác nhau.
Cho số phức z thỏa mãn \(4\left( {\overline z - i} \right) - \left( {3 - i} \right)z = - 1 - 29i.\) Mô đun của z bằng
Cho phương trình \(\log _2^2x - 2{\log _2}x - \sqrt {m + {{\log }_2}x} = m.\) Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 20;20} \right]\) để phương trình đã cho có nghiệm \(x \in \left( {0;1} \right).\)
Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
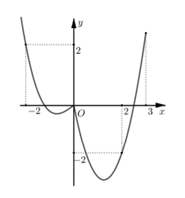
Cho hàm số \(f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) được cho như hình vẽ bên. Hàm số \(y = \left| {f\left( x \right) + \frac{1}{2}{x^2} - f\left( 0 \right)} \right|\) có nhiều nhất bao nhiêu điểm cực trị trong khoảng \(\left( { - 2;3} \right)\)?
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với đáy. Biết rằng \(\left( {SBC} \right)\) tạo với đáy một góc \(45^\circ .\) Thể tích khối cầu ngoại tiếp khối chóp là:
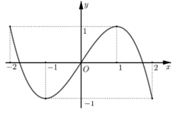
Cho hàm số \(f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) được cho như hình vẽ bên. Hàm số \(y = f\left( {\cos x} \right) + {x^2} - x\) đồng biến trên khoảng
Tập tất cả các số thực x thỏa mãn \({\left( {\frac{2}{3}} \right)^{4x}} \le {\left( {\frac{3}{2}} \right)^{2 - x}}\) là: