Một công ty cần xây dựng một cái kho chứa hàng dạng hình hộp chữ nhật (có nắp) bằng vật liệu gạch và xi măng có thể tích 2000 \[{m^3}\], đáy là hình chữ nhật có chiều dài bằng hai lần chiều rộng. Người ta cần tính toán sao cho chi phí xây dựng là thấp nhất, biết giá xây dựng là 500.000 đồng/\[{m^2}\]. Khi đó chi phí thấp nhất gần với số nào dưới đây?
Giải bởi Vietjack
Đáp án D
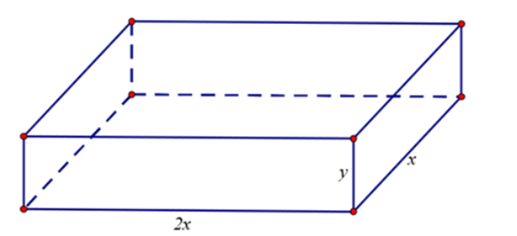
Gọi kích thước đáy của cái kho cần xây dựng là \(x\left( m \right)\) và \(2x\left( m \right),\) chiều cao của kho là \(y\left( m \right),\) (với \(x,y > 0\))
Ta có \(V = 2{x^2}y = 2000 \Rightarrow y = \frac{{1000}}{{{x^2}}}\left( m \right)\)
Diện tích toàn phần của hình hộp chữ nhật là
\({S_{tp}} = 2\left( {x.2x + x.y + 2x.y} \right) = 4{x^2} + 6xy = 4{x^2} + \frac{{6000}}{x}\)
\( = 4{x^2} + \frac{{3000}}{x} + \frac{{3000}}{x} \ge 3\sqrt[x]{{4{x^2}.\frac{{3000}}{x}.\frac{{3000}}{x}}} = 300\sqrt[3]{{36}}\left( {{m^2}} \right)\)
Dấu đẳng thức xảy ra khi và chỉ khi \(4{x^2} = \frac{{3000}}{x} \Leftrightarrow x = \sqrt[3]{{750}}\left( m \right)\)
Chi phí xây dựng thấp nhất khi đó sấp sỉ là \(300\sqrt[3]{{36}}.500000 \approx 495289087\) đồng
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho phương trình \[{\log _3}^2\left( {9x} \right) - \left( {m + 5} \right){\log _3}x + 3m - 10 = 0\]. Số giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc \[\left[ {1;81} \right]\] là
Cho \[\int\limits_0^3 {f\left( x \right)dx} = 2\]. Tính giá trị của tích phân \[L = \int\limits_0^3 {\left[ {2f\left( x \right) - {x^2}} \right]dx} \].
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \[{d_1}:\;\frac{{x - 2}}{{ - 1}} = \frac{{y - 1}}{3} = \frac{{z - 1}}{2}\] và \[{d_2}:\;\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + t\\z = - 1 - t\end{array} \right..\] Phương trình đường thẳng \[\Delta \] nằm trong mặt phẳng \[\left( P \right):\;x + 2y - 3z - 2 = 0\] cắt cả hai đường thẳng \[{d_1}\] và \[{d_2}\] là
Kí hiệu \[{z_1},{z_2},{z_3},{z_4}\] là bốn nghiệm phức của phương trình \[{z^4} + 3{z^2} - 4 = 0.\] Tính tổng \[T = \left| {{z_1}} \right| + {\left| z \right|_2} + \left| {{z_3}} \right| + \left| {{z_4}} \right|.\]
Biết \[\int\limits_4^5 {\frac{{dx}}{{{x^2} + 3x + 2}} = a\ln 2 + b\ln 3 + c\ln 5 + d\ln 7} \] với \[a,b,c,d\] là các số nguyên. Tính \[P = ab + cd.\]
Bất phương trình \[{4^x} - \left( {m + 1} \right){2^{x + 1}} + m \ge 0\] nghiệm đúng với mọi \[x \ge 0\]. Tập tất cả các giá trị của m là
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \[B,AB = 3a,BC = 4a\]. Cạnh bên SA vuông góc với mặt phẳng đáy. Góc tạo bởi giữa SC và mặt phẳng đáy bằng \[{60^0}\]. Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng:
Cho cấp số cộng có \[{u_1} = - 3;{u_{10}} = 24\]. Tìm công sai d?
Cho hàm số f(x) liên tục trên \[\left[ {0;{\mkern 1mu} 1} \right].\] Biết \[\int\limits_0^1 {\left[ {x.{\mkern 1mu} f'\left( {1 - x} \right) - f\left( x \right)} \right]{\mkern 1mu} {\rm{d}}x} = \frac{1}{2},\] tính \[f\left( 0 \right).\]
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):2x - y + z + 4 = 0\]. Khi đó mặt phẳng (P) có một vectơ pháp tuyến là
Có bao nhiêu số phức z thỏa mãn \[\left| {z - 2 + i} \right| = \left| {z + 1 - 2i} \right|\] và \[\left| {z + 4 - 2i} \right| = 3\sqrt 2 ?\]
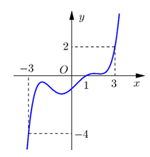
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có đồ thị \[y = f'\left( x \right)\] như hình vẽ. Đặt \[g\left( x \right) = 2f\left( x \right) - {\left( {x - 1} \right)^2}.\] Khi đó giá trị nhỏ nhất của hàm số \[y = g\left( x \right)\] trên đoạn \[\left[ { - 3;3} \right]\] bằng
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng \[x = 1\] và \[x = 4\], biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \[x\] (\[1 \le x \le 4\]) thì được thiết diện là một hình lục giác đều có độ dài cạnh là \[2x\].
