Cho A là tập các số tự nhiên có 7 chữ số. Lấy một số bất kỳ của tập A. Tính xác suất để lấy được số lẻ và chia hết cho 9.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Có tất cả \[9.10.10.10.10.10.10 = {9.10^6}\] số tự nhiên có 7 chữ số.
Ta có \[\overline {abcdefg} \; \vdots \;9 \Leftrightarrow \left( {a + b + c + d + e + f + g} \right) \vdots 9\]. Các số lẻ chia hết cho 9 là 1000017, 1000035, 100053,…,9999999.
Đây là một cấp số cộng có \[{u_1} = 1000017\] và công sai \[d = 18\].
Số phần tử của dãy này là \[\frac{{999999 - 1000017}}{{18}} + 1 = 500000\].
Vậy xác suất cần tìm là \[\frac{{500000}}{{{{9.10}^6}}} = \frac{1}{{18}}.\]
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho \[a,{\rm{ }}b\] là các số thực dương thỏa mãn \[{a^2} + {b^2} = 8ab.\] Mệnh đề nào dưới đây là đúng?
Biết rằng \[\int\limits_2^3 {\frac{{x + 1}}{{x\left( {x - 2} \right) + 1}}dx} = a + b\ln 2,\] với \[a,{\rm{ }}b \in \mathbb{Z}.\] Tính \[S = a + 2b.\]
Tính thể tích của khối lập phương \[ABCD.A'B'C'D'\], biết \[AC' = 2a\sqrt 3 .\]
Cho hàm số \[y = {x^3} - 3m{x^2} + 3\left( {2{m^2} - 10m + 9} \right)x\]. Có bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có hai điểm cực trị?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, \[AC = \frac{{a\sqrt 2 }}{2}.\] Cạnh bên SA vuông góc với mặt phẳng đáy và đường thẳng SB tạo với mặt phẳng \[\left( {ABCD} \right)\] một góc \[60^\circ .\] Khoảng cách giữa hai đường thẳng \[AD\] và \[SC\] bằng
Tính môđun của số phức z thỏa mãn \[z\left( {1 - i} \right) + 2i = 1.\]
Tìm số tiệm cận đứng của đồ thị hàm số \[y = \frac{{\sqrt {x + 1} + \sqrt {x + 4} - 3}}{{{x^3} - x}}.\]
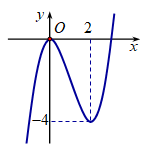
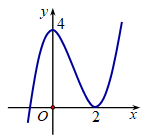
Cho hàm số f(x) có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số \[y = f\left[ {f\left( x \right)} \right]\].
Cho hàm số f(x) có bảng biến thiên như sau:
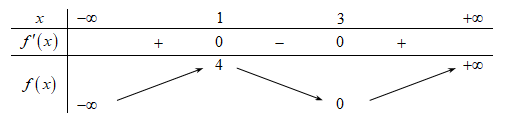
Phương trình \[3f\left( x \right) - 2 = 0\] có số nghiệm thực là
Trong không gian Oxyz, cho hai đường thẳng \[{d_1}:\frac{{x - 1}}{1} = \frac{y}{1} = \frac{{z - 1}}{{ - 1}}\] và \[{d_2}:\frac{{x + 4}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z + 3}}{1}.\] Mặt phẳng \[\left( Q \right):ax + by + cz - 4 = 0\] chứa đường thẳng \[{d_1}\] và song song với đường thẳng \[{d_2}.\] Tính \[a + b + c.\]
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):x + 2y - 3z + 3 = 0.\] Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Tập nghiệm của phương trình \[\frac{1}{2}{\log _3}{\left( {x + 2} \right)^2} + \frac{1}{3}{\log _3}{\left( {4x - 1} \right)^3} = 2\] là
Cho hai số phức z, w thỏa mãn \[\left| {z + 2w} \right| = 3\], \[\left| {2z + 3w} \right| = 6\] và \[\left| {z + 4w} \right| = 7\]. Tính giá trị của biểu thức \[P = z.\bar w + \bar z.w\].
Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và đồ thị hàm số \[y = f'\left( x \right)\] như hình vẽ. Bất phương trình \[f\left( x \right) > {x^3} + 4x + m\] nghiệm đúng với mọi \[x \in \left( {0;2} \right)\] khi và chỉ khi
Cho hàm số \[y = f\left( x \right)\] có đạo hàm tại \[x = 1\] và \[f'\left( 1 \right) \ne 0.\] Gọi \[{d_1}\], \[{d_2}\] lần lượt là hai tiếp tuyến của đồ thị hàm số \[y = f\left( x \right)\] và \[y = g\left( x \right) = x.f\left( {2x - 1} \right)\] tại điểm có hoành độ \[x = 1.\] Biết rằng hai đường thẳng \[{d_1}\], \[{d_2}\] vuông góc với nhau. Khẳng định nào sau đây đúng?