Cho hàm số $f\left(x\right)$ liên tục và nhận giá trị dương trên $\left[0;1\right].$ Biết $f\left(x\right).f\left(1-x\right)=1$ với $\forall x\in \left[0;1\right].$  Tính giá trị  $I=\underset{0}{\overset{1}{\int }}\frac{dx}{1+f\left(x\right)}$

Tập nghiệm của bất phương trình ${\log }_1\frac{1-2\text{x}}{x}>0$ là

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Mặt phẳng $\left(\alpha \right)$  đi qua A, B và trung điểm M của SC. Mặt phẳng $\left(\alpha \right)$ chia khối chóp đã cho thành hai phần có thể tích lần lượt là $V_1,V_2$  với $V_1<V_2.$   Tính tỉ số  $\frac{V_1}{V_2}.$

Tìm giá trị của tham số m sao cho đồ thị của hàm số $\mathrm{y}={\mathrm{x}}^3-3{\mathrm{x}}^2+\mathrm{m}$ nhận điểm A(1;3) làm tâm đối xứng

 Trong không gian vói hệ tọa độ Oxyz, đường thẳng đi qua điểm $\mathrm{A}\left(1;4;-7\right)$ và vuông góc với mặt phẳng $\left(\mathrm{P}\right):\mathrm{x}+2\mathrm{y}-2\mathrm{z}-3=0$ có phương trình là

 Cho cấp số cộng có  ${\text{u}}_1=2018,\mathrm{d}=-3.$Khi đó ${\mathrm{u}}_2$ bằng

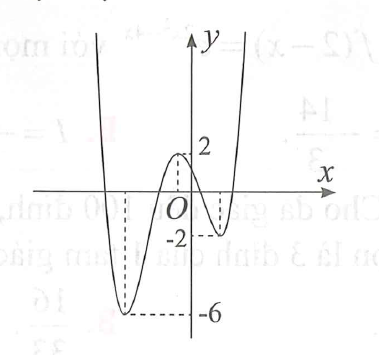
Cho đồ thị hàm số $y=f\left(x\right)$ như hình vẽ dưới đây. Có bao nhiêu giá trị nguyên của tham số m để hàm số$y=\left[f\left(x+2018\right)+m^2\right]$ có 5 điểm cực trị?

Tìm tập xác định của hàm số  $y={\log }_2\left(2x^2-x-1\right)$

 Cho hình nón có bán kính đáy $\mathrm{r}=\sqrt{3}$ và độ dài đường sinh $\mathrm{l}=4.$ Tính diện tích xung quanh ${\mathrm{S}}_{\mathrm{xq}}$ của hình nón đã cho.

 Một khối trụ có bán kính R, chiều cao h và thể tích V₁ Tăng bán kính đáy lên gấp đôi, chiều cao khối trụ không đổi thì thể tích khối trụ khi đó

Tìm phần ảo của số phức $\mathrm{z}=2\mathrm{i}\left(2-\mathrm{i}\right).$ 

Tìm tất cả các giá trị của tham số m để hàm số $y=\frac{2\cos x+3}{2\cos x-m}$ nghịch biến trên khoảng $\left(0;\frac{\pi }{3}\right).$   

Cho tập $X=\left\{\mathrm{1,2,3,4,5,6,7,8,9}\right\}.$ Hỏi có tất cả bao nhiêu mệnh đề đúng trong các mệnh đề sau

(I) “Có $A_9^4$ số có 4 chữ số được lập từ tập X”

(II) “ $A_{10}^5$ là một tổ hợp chập 3 của X”

(III) “Mỗi hoán vị các phần tử của X là một chỉnh hợp chập 9 của X”

Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau?

Hàm số nào sau đây đồng biến trên khoảng $\left(-\infty ;+\infty \right)$ 

Biết F(x) là nguyên hàm của $\mathrm{f}\left(\mathrm{x}\right)=4{\mathrm{x}}^3-\frac{1}{{\mathrm{x}}^2}+3\mathrm{x}$ thỏa mãn $5\mathrm{F}\left(1\right)+\mathrm{F}\left(2\right)=43$ Tính F(2)