Trong không gian với hệ tọa độ Oxyz, cho các đường thẳng và đường thẳng Viết phương trình đường thẳng đi qua cắt d1 và d2 vuông góc
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C.
Ta có:
Gọi
Do
Vậy
Phương trình đường thẳng cần tìm là:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ và Giá trị của biểu thức bằng
Cho hàm số bậc bốn y=f(x) có đồ thị như hình vẽ dưới đây.
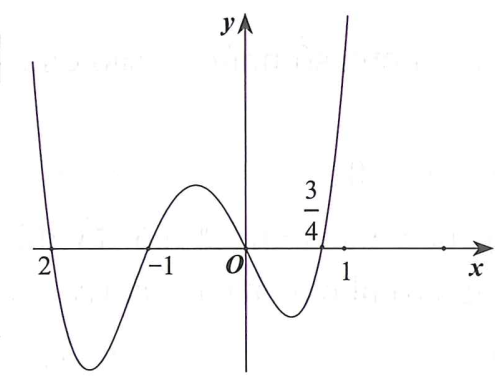
Số điểm cực trị của hàm số là
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm có vectơ pháp tuyến là:
Cho khối cầu (S) ngoại tiếp tứ diện OABC có OA = OB = OC = a và OA, OB, OC đôi một vuông góc. Thể tích của (S) bằng

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
Hệ thức liên hệ giữa giá trị cực đại và giá trị cực tiểu của hàm số là