Một hộp chứa 5 bi trắng, 6 bi đỏ và 7 bi xanh, tất cả các bi có kích thước và khối lượng như nhau. Chọn ngẫu nhiên 6 bi từ hộp đó. Tính xác suất để 6 bi lấy được có đủ ba màu đồng thời hiệu của số bi đỏ và trắng, hiệu của số bi xanh và đỏ, hiệu của số bi trắng và xanh theo thứ tự lập thành cấp số cộng
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Số phần tử của không gian mẫu chính là số cách lấy ngẫu nhiên 6 viên bi bất kì trong 18 viên nên .
Gọi A là biến cố “6 bi lấy được có đủ ba màu đồng thời hiệu của số bi đỏ và trắng, hiệu của số bi xanh và đỏ, hiệu của số bi trắng và xanh tạo thành cấp số cộng”.
Gọi lần lượt là số bi trắng, bi đỏ và bi xanh trong 6 viên bi được chọn ra.
Theo đề bài ta có: lập thành một cấp số cộng.
Do đó: . Lại có nên ta có các trường hợp.
Trường hợp 1: và . Khi đó số cách chọn 6 viên bi là cách.
Trường hợp 2: . Khi đó số cách chọn 6 viên bi là cách.
Vậy số phần tử của biến cố A là .
Do đó xác suất của biến cố A là .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
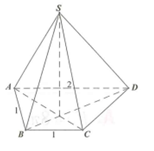
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; AB=BC=1 , AD=2 . Các mặt chéo (SAC) và (SBD) cùng vuông góc với mặt đáy (ABCD) . Biết góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 60 độ (tham khảo hình vẽ bên). Khoảng cách từ điểm D đến mặt phẳng (SAB) là
Cho 3 số phức thỏa mãn , , . Tính giá trị nhỏ nhất của biểu thức .
Cho là các hàm số có đạo hàm liên tục trên R, số và C là một hằng số tùy ý. Xét 4 mệnh đề sau
(I):
(II):
(III):
(IV):
Số mệnh đề đúng là
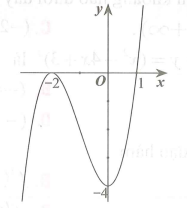
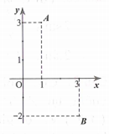
Gọi A, B lần lượt 2 điểm biểu diễn số phức trong mặt phẳng phức ở hình vẽ bên. Tính .
Trong không gian Oxyz, cho đường thẳng và mặt phẳng . Đường thẳng nằm trong mặt phẳng , cắt và vuông góc với đường thẳng d có phương trình là