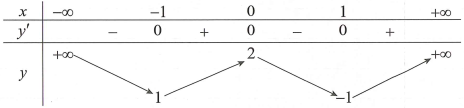
Cho hàm số có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của m ( ) sao cho . Số phần tử của tập S là
![Cho hàm số f(x)= ã^3+bx^2+cx+d có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của m ( m thuộc R) sao cho (x-1)[m^3f(2x-1)-mf(x)+f(x+1)]>=0, với mọi x thuộc R . Số phần tử của tập S là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/06/screenshot-2022-06-15-225048-1655308048.png)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Từ giả thiết suy ra: .
Với ta có: (đúng)
Với ta có: (đúng)
Với .
Xét ta có:
đủ lớn sao cho
(mâu thuẫn (*)) (loại).
Vậy .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
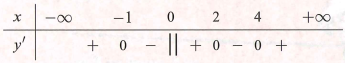
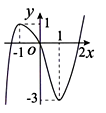
Hàm số đã cho có bao nhiêu điểm cực trị?
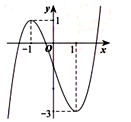
Cho hàm số liên tục trên R và có đồ thị như hình vẽ. Số nghiệm thực của phương trình là:
Cho a, b, c theo thứ tự này là ba số hạng liên tiếp của một cấp số cộng. Biết . Giá trị của b bằng:
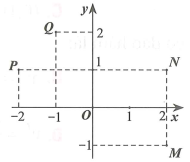
Cho . Điểm nào trong hình vẽ bên dưới là điểm biểu diễn số phức ?
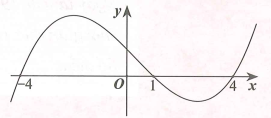
Khẳng định nào dưới đây sai?
Gọi S là tập hợp tất cả các giá trị thực của m để tồn tại 4 số phức z thỏa mãn và là số thuần ảo. Tổng các phần tử của S là:
Bán kính của mặt cầu ngoại tiếp chóp đều S.ABC có tất cả các cạnh bằng a là:
Với , trong đó a, b là các số thực dương tùy ý và a khác 1. Khi đó mệnh đề nào dưới đây đúng?
Cho hình lăng trụ và M, N là hai điểm lần lượt bên cạnh CA, CB sao cho MN song song với AB và . Mặt phẳng chia khối lăng trụ thành hai phần có thể tích (phần chứa điểm C) và sao cho . Khi đó giá trị của k là: