Gọi (H) là hình phẳng giới hạn bởi parabol , cung tròn và trục hoành (phần tô đậm trong hình vẽ). Diện tích của hình bằng
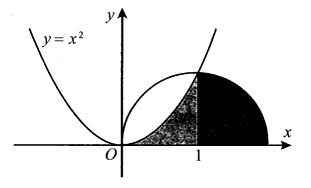
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
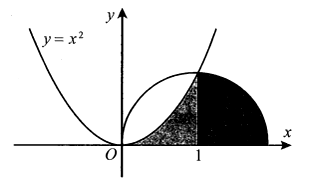
Phương trình hoành độ giao điểm giữa parabol và cung tròn: .
Khi đó: .
Đặt .
Đổi cận: .
Suy ra .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
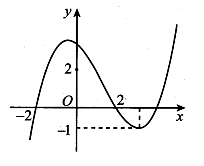
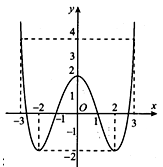
Cho hàm số bậc ba có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình có 10 nghiệm phân biệt?
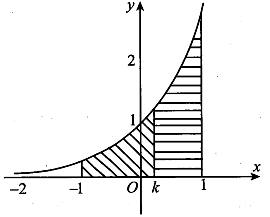
Cho hàm số có đồ thị như hình vẽ bên. Gọi là diện tích hình phẳng giới hạn bởi các đường và là diện tích hình phẳng giới hạn bởi các đường . Xác định k để .
Cho hàm số có đồ thị như hình vẽ. Số các giá trị nguyên của tham số m để đồ thị hàm số có tổng số 9 đường tiệm cận ngang và tiệm cận đứng là
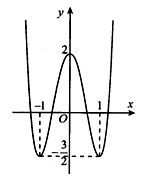
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Tìm tham số a để hàm số y=|f(x)+a| có ba điểm cực trị.
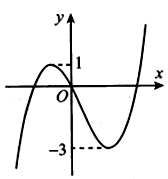
Xét số phức z thỏa mãn . Gọi P; p tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của |z|. Giá trị của bằng
Cho hàm số f(x) có đạo hàm liên tục trên [-1;1] và thỏa mãn f(1) = 0, với mọi x thuộc
Gọi là số nguyên để phương trình ,
có hai nghiệm phân biệt thỏa mãn . Với đó giá trị của biểu thức thuộc vào khoảng nào dưới đây?
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây:
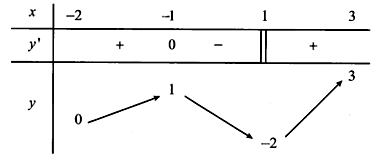
Khẳng định nào sau đây sai?
Trong không gian Oxyz, cho điểm và đường thẳng . Đường thẳng đi qua M, cắt và vuông góc với d có phương trình là