Cho số tự nhiên \(n\) thỏa mãn \(C_n^0 + C_n^1 + C_n^2 = 11.\) Số hạng chứa \({x^7}\) trong khai triển \({\left( {{x^3} - \frac{1}{{{x^2}}}} \right)^n}\) bằng
A. \( - 4.\)
B.\( - 12{x^7}.\)
C.\(9{x^7}.\)
D. \( - 4{x^7}.\)
Giải bởi Vietjack
Với \(n \ge 2,n \in \mathbb{N}*\) ta có:
\(n = 4 \Rightarrow {\left( {{x^3} - \frac{1}{{{x^2}}}} \right)^n} = {\left( {{x^3} - \frac{1}{{{x^2}}}} \right)^4}\)
\({\left( {{x^3} - \frac{1}{{{x^2}}}} \right)^4} = \sum\limits_{k = 0}^4 {C_4^k.{{\left( {{x^3}} \right)}^{4 - k}}.\frac{{{{\left( { - 1} \right)}^k}}}{{{{\left( {{x^2}} \right)}^k}}} = } \sum\limits_{k = 0}^4 {{{\left( { - 1} \right)}^k}.C_4^k.{x^{12 - 5k}}\left( {0 \le k \le 4,k \in \mathbb{N}} \right)} \)
Số hạng tổng quát \({\left( { - 1} \right)^k}C_4^k.{x^{12 - 5k}}\)
Phải có \({x^{12 - 5k}} = {x^7} \Rightarrow 12 - 5k = 7 \Leftrightarrow k = 1.\)
Số hạng chứa \({x^7}\) trong khai triển là: \({\left( { - 1} \right)^1}C_4^1.{x^7} = - 4{x^7}.\)
Đáp án D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
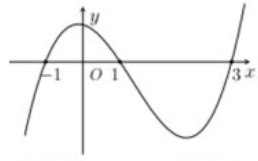
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}.\) Biết hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Gọi \(S\) là tập hợp các giá trị nguyên \(m \in \left[ { - 2021;2021} \right]\) để hàm số \(g\left( x \right) = f\left( {x + m} \right)\) nghịch biến trên khoảng \(\left( {1;2} \right).\) Hỏi \(S\) có bao nhiêu phần tử?
Cho hàm số \(y = {x^4} - 2m{x^2} + m,\) có đồ thị \(\left( C \right)\) với \(m\) là tham số thực. Gọi \(A\) là điểm thuộc đồ thị \(\left( C \right)\) có hoành độ bằng 1. Tìm \(m\) để tiếp tuyến \(\Delta \) với đồ thị \(\left( C \right)\) tại \(A\) cắt đường tròn tạo thành một dây cung có độ dài nhỏ nhất.
Cho hình chóp \(S.ABC\) có \(AB = AC = 4,BC = 2,SA = 4\sqrt 3 ;\angle SAB = \angle SAC = {30^0}.\) Gọi \({G_1},{G_2},{G_3}\) lần lượt là trọng tâm của các tam giác \(\Delta SBC;\Delta SCA;\Delta SAB\) và \(T\) đối xứng \(S\) qua mặt phẳng \(\left( {ABC} \right).\) Thể tích của khối chóp \(T.{G_1}{G_2}{G_3}\) bằng \(\frac{a}{b}\) với \(a,b \in \mathbb{N}\) và \(\frac{a}{b}\) tối giản. Tính giá trị \(P = 2a - b.\)
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {n^2} + n + 1\) với \(n \in \mathbb{N}*\). Số 21 là số hạng thứ bao nhiêu của dãy số đã cho?
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác \(ABC\) vuông tại \(B;AB = 2a,BC = a,AA' = 2a\sqrt 3 .\) Thể tích khối lăng trụ \(ABC.A'B'C'\) là
Cho tứ diện đều \(ABCD,M\) là trung điểm của \(BC.\) Khi đó cosin của góc giữa hai đường thẳng nào sau đây có giá trị bằng \(\frac{{\sqrt 3 }}{6}?\)
Cho hình chóp \(S.ABC\) có cạnh \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right),\) biết \(AB = AC = a,BC = a\sqrt 3 .\) Tính góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right).\)
Có bao nhiêu giá trị nguyên của tham số \(m\) trong \(\left[ { - 2020;2020} \right]\) để phương trình \(\log \left( {mx} \right) = 2\log \left( {x + 1} \right)\) có nghiệm duy nhất?
Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm thuộc đồ thị hàm số \(y = {\log _3}x.\) Tìm điều kiện của \({x_0}\) để điểm \(M\) nằm phía trên đường thẳng \(y = 2.\)
Gọi \(\left( S \right)\) là tập hợp các giá trị nguyên \(m\) để đồ thị hàm số \(y = \left| {3{x^4} - 8{x^3} - 6{x^2} + 24x - m} \right|\) có 7 điểm cực trị. Tính tổng các phần tử của \(S.\)
Cho hình trụ có bán kính đáy bằng \(a\) và chiều cao gấp 2 lần đường kính đáy của hình trụ. Tính diện tích xung quanh của hình trụ.
Cho mặt cầu \(S\left( {O;r} \right)\), mặt phẳng \(\left( P \right)\) cách tâm \(O\) một khoảng bằng \(\frac{r}{2}\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là một đường tròn. Hãy tính theo \(r\) chu vi của đường tròn là giao tuyến của mặt phẳng \(\left( P \right)\) và mặt cầu \(\left( S \right).\)
Tính tổng tất cả các nghiệm của phương trình \({5^{{{\sin }^2}x}} + {5^{{{\cos }^2}x}} = 2\sqrt 5 \) trên đoạn \(\left[ {0;2\pi } \right].\)
