Bất phương trình \(x\sqrt {x + 1} \le \left( {2x - 3} \right){.2^{\frac{{ - {x^3} + 16{x^2} - 48x + 36}}{{{x^2}}}}}\) có bao nhiêu nghiệm nguyên?
A. 8.
B. 10.
C. 9.
D. Vô số.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A.
Điều kiện: \(\left\{ \begin{array}{l}x \ge - 1\\x \ne 0\end{array} \right..\)
Ta chỉ xét với các giá trị nguyên của \(x.\)
Với \(x = \pm 1\) thay vào bất phương trình không thỏa mãn.
Với \(x \ge 2,\) bất phương trình tương đương với:
\(2x\sqrt {x + 1} \le \left( {4x - 6} \right){.2^{\frac{{16{x^2} - 48x + 36}}{{{x^2}}} - x}} \Leftrightarrow \sqrt {x + 1} {.2^{{{\left( {\sqrt {x + 1} } \right)}^2}}} \le \frac{{4x - 6}}{x}{.2^{{{\left( {\frac{{4x - 6}}{x}} \right)}^2}}}\left( * \right)\)
Xét hàm số \(f\left( t \right) = {2^{{t^2}}}.t\) trên khoảng \(\left( {0; + \infty } \right)\) ta có: \(f'\left( t \right) = {2^{{t^2}}} + 2{t^2}{.2^{{t^2}}}.\ln 2 >0,\forall t >0.\)
Vậy hàm số \(f\left( t \right)\) đồng biến trên khoảng \(\left( {0; + \infty } \right),\) khi đó:
\(\left( * \right) \Leftrightarrow f\left( {\sqrt {x + 1} } \right) \le f\left( {\frac{{4x - 6}}{x}} \right) \Leftrightarrow \sqrt {x + 1} \le \frac{{4x - 6}}{x}\)
\( \Leftrightarrow {x^2}\left( {x + 1} \right) \le 16{x^2} - 48x + 36 \Leftrightarrow {x^3} - 15{x^2} + 48x - 36 \le 0\)
\( \Leftrightarrow \left( {x - 3} \right)\left( {{x^2} - 12x + 12} \right) \le 0 \Leftrightarrow \left[ \begin{array}{l}x \le 6 - 2\sqrt 5 \left( { \approx 1,101} \right)\\3 \le x \le 6 + 2\sqrt 5 \left( { \approx 10,898} \right)\end{array} \right..\)
Vậy bất phương trình có 8 nghiệm nguyên.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
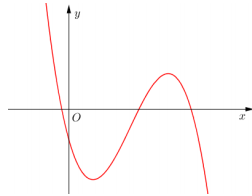
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) đồ thị là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
Cho hai hàm số \(y = {2^x}\) và \(y = {\log _2}x\) lần lượt có đồ thị \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\) Gọi \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\) là hai điểm lần lượt thuộc \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) sao cho tam giác \(IAB\) vuông cân tại \(I,\) trong đó \(I\left( { - 1; - 1} \right).\) Giá trị của \(P = \frac{{{x_A} + {y_A}}}{{{x_B} + {y_B}}}\) bằng
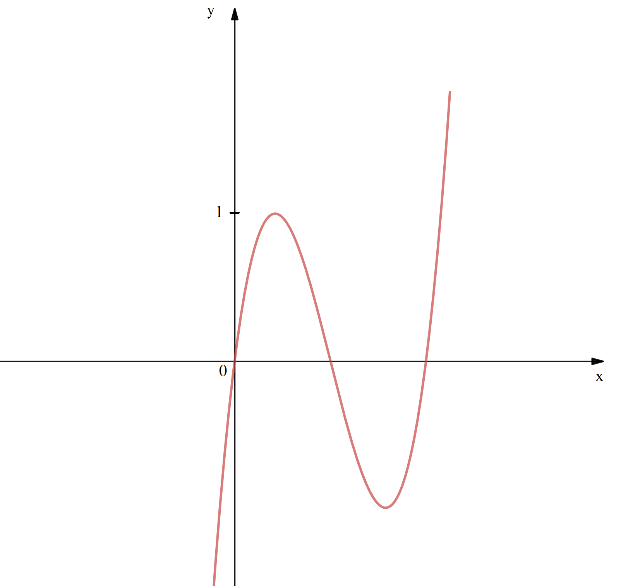
Cho hàm số \[f(x)\] có \[f(0) = 0\]. Biết rằng \[y = f'(x)\] là hàm số bậc ba và có đồ thị là đường cong trong hình dưới đây, hàm số \[g(x) = f(f(x) - x)\] có bao nhiêu điểm cực trị ?
Trong các hàm số dưới đây, hàm số nào nghịch biến trên khoảng \(\mathbb{R}?\)
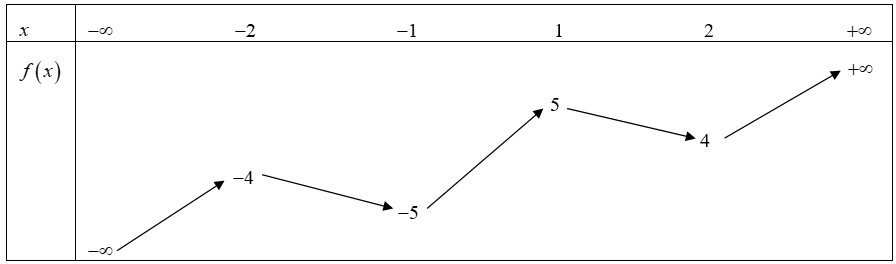
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số \(m\) để trên đoạn \(\left[ { - 1;2} \right]\) phương trình \(3f\left( {{x^2} - 2x - 1} \right) = m\) có đúng hai nghiệm thực phân biệt?
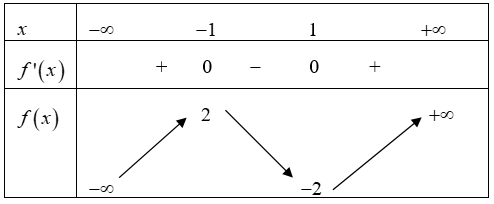
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Số nghiệm thực của phương trình \(3f\left( x \right) + 1 = 0\) là
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} - 36x\) trên đoạn \(\left[ {2;20} \right]\) bằng