Cho hình trụ có bán kính bằng \(\sqrt 5 .\) Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được là một hình vuông. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
A.\(10\pi .\)
B.\(\frac{{20\pi }}{3}.\)
C.\(20\pi .\)
D.\(\frac{{10\pi }}{3}.\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C.
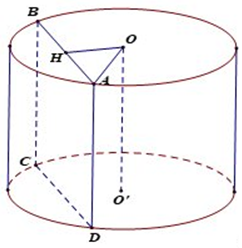
Gọi thiết diện thu được là hình vuông \(ABCD\)
Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB\)
Mặt khác \(AD \bot OH\)
\( \Rightarrow OH \bot \left( {ABCD} \right)\)
Ta có \(OO'//\left( {ABCD} \right) \Rightarrow d\left( {OO';\left( {ABCD} \right)} \right) = d\left( {O,\left( {ABCD} \right)} \right) = OH = 1\)
\(HA = \sqrt {O{A^2} - O{H^2}} = 2 \Rightarrow AB = 4 \Rightarrow AD = 4\)
Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
\(V = \pi .OA'.AD = \pi .{\left( {\sqrt 5 } \right)^2}.4 = 20\pi .\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
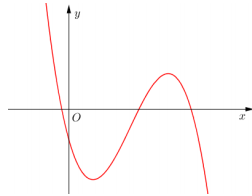
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) đồ thị là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
Cho hai hàm số \(y = {2^x}\) và \(y = {\log _2}x\) lần lượt có đồ thị \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\) Gọi \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\) là hai điểm lần lượt thuộc \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) sao cho tam giác \(IAB\) vuông cân tại \(I,\) trong đó \(I\left( { - 1; - 1} \right).\) Giá trị của \(P = \frac{{{x_A} + {y_A}}}{{{x_B} + {y_B}}}\) bằng
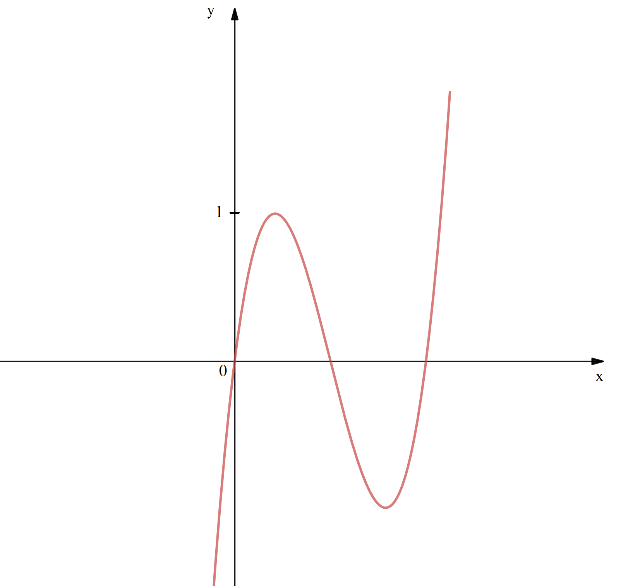
Cho hàm số \[f(x)\] có \[f(0) = 0\]. Biết rằng \[y = f'(x)\] là hàm số bậc ba và có đồ thị là đường cong trong hình dưới đây, hàm số \[g(x) = f(f(x) - x)\] có bao nhiêu điểm cực trị ?
Trong các hàm số dưới đây, hàm số nào nghịch biến trên khoảng \(\mathbb{R}?\)
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
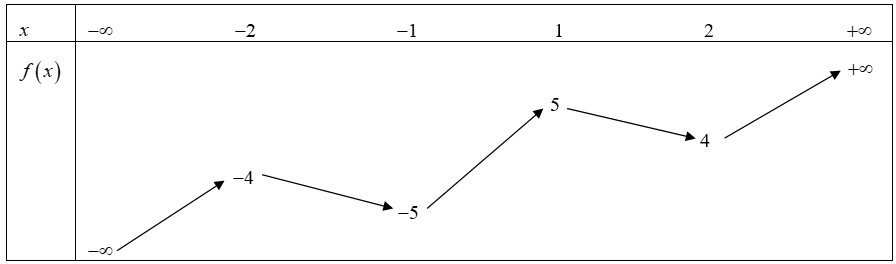
Có bao nhiêu giá trị nguyên của tham số \(m\) để trên đoạn \(\left[ { - 1;2} \right]\) phương trình \(3f\left( {{x^2} - 2x - 1} \right) = m\) có đúng hai nghiệm thực phân biệt?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
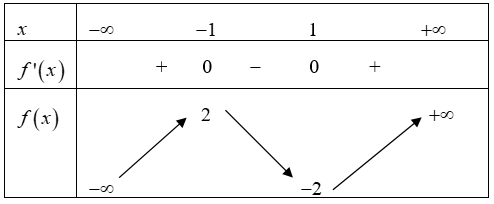
Số nghiệm thực của phương trình \(3f\left( x \right) + 1 = 0\) là
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} - 36x\) trên đoạn \(\left[ {2;20} \right]\) bằng