Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, cạnh BC = 2a và Biết tứ giác BCC'B' là hình thoi có là góc nhọn. Mặt phẳng (BCC'B') vuông góc với (ABC) và mặt phẳng (ABB'A') tạo với mặt phẳng (ABC) một góc Thể tích khối lăng trụ ABC.A'B'C' bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
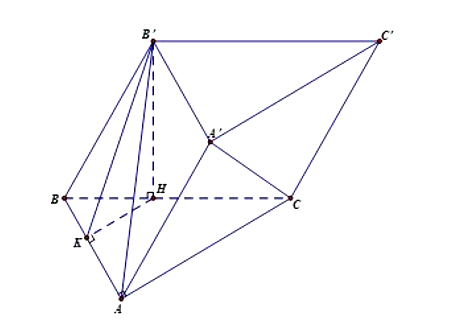
Kẻ tại H (do là góc nhọn nên H thuộc đoạn tại K và giả sử B'H = x với x > 0.
Ta có:
Do nên .
Từ đó suy ra vuông cân tại H.
Trong tam giác BKH vuông tại K có:
Do tứ giác BCC'B' là hình thoi nên BB' = BC = 2a
Trong tam giác B'HB vuông tại H có:
Trong tam giác ABC vuông tại A có:
Vậy thể tích khối lăng trụ ABC.A'B'C' là
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
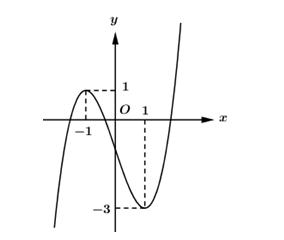
Cho hàm số y = f(x) là hàm đa thức bậc ba có đồ thị như hình vẽ bên dưới. Khẳng định nào sau đây là sai?
Cho hàm số với m là tham số thực. Tìm tất cả các giá trị của ![]() để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.
để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và Thể tích của khối tứ diện đó là
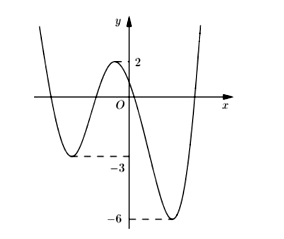
Cho y = f(x) là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-12; 12] để hàm số có 5 điểm cực trị?
Điều kiện cần và đủ để hàm số có hai điểm cực đại và một điểm cực tiểu là
Hình nón có đường sinh l = 2a và hợp với đáy góc Diện tích toàn phần của hình nón bằng
Xếp ngẫu nhiên 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C vào sáu ghế quanh một bàn tròn (mỗi học sinh ngồi đúng một ghế). Tính xác suất để học sinh lớp C ngồi giữa 2 học sinh lớp B