Một lớp có 38 học sinh, trong đó có 20 học sinh nam. Chọn ngẫu nhiên một học sinh. Tính xác suất để chọn được một học sinh nữ.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B.
Xét phép thử: “Chọn ngẫu nhiên một học sinh từ 38 học sinh trong lớp”
Gọi biến cố A: “Chọn được một học sinh nữ”
Trong lớp có 18 học sinh nữ, nên có (cách) chọn một học sinh nữ.
Vậy
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz, cho hai điểm Phương trình mặt phẳng trung trực của đoạn thẳng AB là:
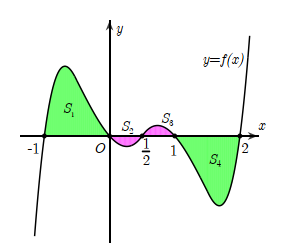
Cho hàm số y = f(x) liên tục trên có đồ thị tạo với trục hoành các miền có diện tích (như hình vẽ) và Biết tích phân với là phân số tối giản. Tính tích ab?
Trong không gian tọa độ Oxyz, phương trình mặt phẳng (P) đi qua điểm M(1; 1; 1) và có vectơ pháp tuyến là:
Cho hàm số f(x) có bảng xét dấu của đạo hàm f'(x) như sau:
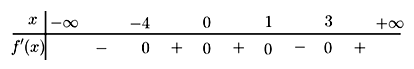
Số điểm cực trị của hàm số f(x) đã cho là:
Biết giá trị lớn nhất của hàm số trên đoạn [0; 2] bằng 5, tìm giá trị của tham số m
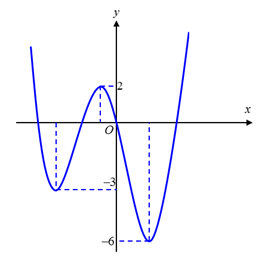
Cho hàm số f(x) liên tục trên và đồ thị hàm số y = f(x) cắt trục hoành tại các điểm có hoành độ lần lượt là (như hình bên dưới). Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số trên [a; c] bằng 2021. Tổng tất cả các phần tử của S bằng:
Cho hai số phức thỏa mãn và Gọi số phức z = a + bi thỏa mãn 3a - 2b = 12. Giá trị nhỏ nhất của bằng
Cho hàm số f(x) có bảng biến thiên như sau:
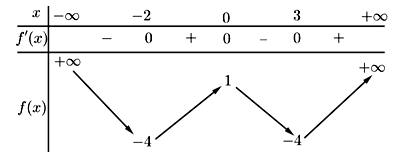
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây?
Trong không gian tọa độ Oxyz, cho ba điểm và C(0; 2; 3). Trọng tâm G của tam giác ABC có tọa độ là: