Tìm tất cả các giá trị của a để bất phương trình ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\)
A. a = 0;
B. a < 0;
C. \(0 < a \le \frac{1}{2}\).
D. \(a \ge \frac{1}{2}\).
Giải bởi Vietjack
Đáp án đúng là: D
ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\) \( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta = {\left( { - 1} \right)^2} - 4.a.a \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\1 - 4{a^2} \le 0\end{array} \right.\)
Xét tam thức bậc hai f(a) = 1 – a2, có ∆ = 02 – 4.(-4).1 = 16 > 0. Do đó f(a) có hai nghiệm phân biệt \(a = \frac{1}{2}\) và \(a = - \frac{1}{2}\)
Ta có bảng xét dấu
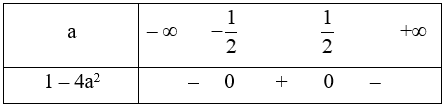
Dựa vào bảng xét dấu ta có 1 – 4a2 ≤ 0 \( \Leftrightarrow a \in \left( { - \infty ; - \frac{1}{2}} \right] \cup \left[ {\frac{1}{2}; + \infty } \right)\).
Kết hợp với điều kiện a > 0 suy ra a ∈ \(\left[ {\frac{1}{2}; + \infty } \right)\).
Vậy để ax2 – x + a ≥ 0, \(\forall x \in \mathbb{R}\) thì a ∈ \(\left[ {\frac{1}{2}; + \infty } \right)\) hay a ≥ \(\frac{1}{2}\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng \(\forall x \ge 3\)?
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x2 + 12x + 36 là:
Các giá trị m làm cho biểu thức f(x) = x2 + 4x + m – 5 luôn dương là:
Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
Cho hàm số f(x) = mx2 – 2mx + m + 1. Giá trị của m để f(x) > 0, \(\forall x \in \mathbb{R}\).
Phương trình x2 – 2(m – 1)x + m – 3 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
Bất phương trình: \[\left( {{x^2} - 3x - 4} \right).\sqrt {{x^2} - 5} < 0\] có bao nhiêu nghiệm nguyên dương?
Bài 17: Dấu của tam thức bậc hai
