Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng \(\forall x \ge 3\)?
A. m ≥ – 11;
B. m > – 11;
C. m < – 11;
D. m < 11.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Ta có: a = 2 > 0. Do đó, 2x2 – 4x + m + 5 > 0, \(\forall x \ge 3\) sẽ có trường hợp sau:
Trường hợp 1. ∆ < 0 \( \Leftrightarrow \) (– 4)2 – 4.2.(m + 5) < 0 \( \Leftrightarrow \) m > – 3, khi đó
2x2 – 4x + m + 5 > 0 với \(\forall x \in \mathbb{R}\).
Do đó 2x2 – 4x + m + 5 > 0 với \(\forall x \ge 3\).
Trường hợp 2. ∆ ≥ 0, khi đó phương trình 2x2 – 4x + m + 5 = 0 sẽ có hai nghiệm x1; x2.
Do đó, để 2x2 – 4x + m + 5 > 0, \(\forall x \ge 3\)\[ \Leftrightarrow \left\{ \begin{array}{l}\Delta \ge 0\\{x_1} \le {x_2} < 3\end{array} \right.\]
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta \ge 0\\a\,f\left( 3 \right) > 0\\\frac{S}{2} < 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \le - 3\\2\left( {{{2.3}^2} - 4.3 + m + 5} \right) > 0\\1 < 3\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \le - 3\\m > - 11\end{array} \right.\)\( \Leftrightarrow \). – 11 < m ≤ – 3
Kết hợp hai trường hợp lại ta được m > – 11 thì thì 2x2 – 4x + m + 5 > 0 với \(\forall x \ge 3\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
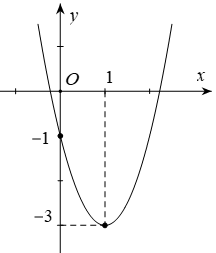
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
Phương trình x2 – (m – 1)x + m2 – 3m + 2 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x ∈ ℝ.
Tập xác định của hàm số \[y = \frac{{x - 1}}{{{x^2} - x + 3}}\] là
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
Bất phương trình: \[\left( {{x^2} - 3x - 4} \right).\sqrt {{x^2} - 5} < 0\] có bao nhiêu nghiệm nguyên dương?
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
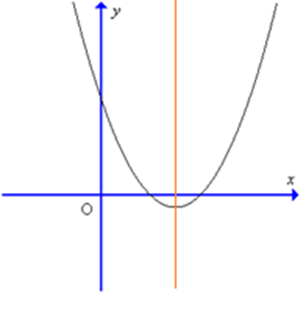
Kết luận nào sau đây đúng về hệ số a, b:
Cho hàm số y = f(x) có đồ thị như hình sau:
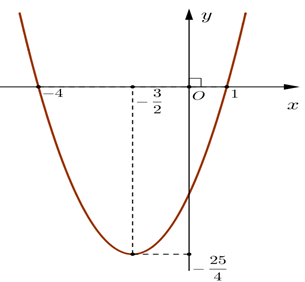
Hàm số đồng biến trên khoảng
Bài tập cuối chương VI