Cho đường thẳng d và điểm O cố định không thuộc d, M là điểm di động trên d. Tìm tập hợp điểm N sao cho tam giác MON đều.

Cho số phức $z=x+yi\left(x,y\in \mathrm{ℝ}\right)$. Tập hợp các điểm biểu diễn của số phức z sao cho số phức $\frac{z+i}{z-i}$ là một số thực âm là:

Tính tổng $S=\frac{1}{2!2017!}+\frac{1}{4!2015!}+\frac{1}{6!2013!}+...+\frac{1}{2016!3!}+\frac{1}{2018!}$ theo n ta được:

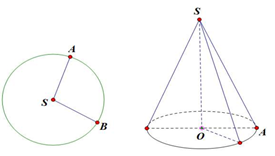
Cho hình tròn tâm S, bán kính R = 2 . Cắt đi $\frac{1}{4}$ hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích toàn phần của hình nón đó.

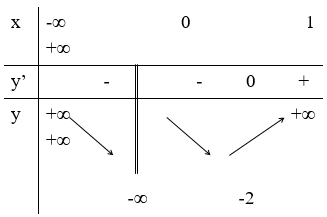
Cho hàm số f (x) có bảng biến thiên dưới đây. Mệnh đề nào sau đây là sai?

Đặt ${\log }_{2}3=a, {\log }_{3}4=b$. Biểu diễn $T={\log }_{27}8+{\log }_{256}81$ theo a và b ta được $T=\frac{x{a}^2+y{b}^2+4}{z{a}^{2}b+a{b}^2}$ với x, y, z là các số thực. Hãy tính tổng $4x^2+y-z^3$.

Gọi $z_1,z_2$ là các nghiệm của phương trình $z^2-4z+9=0$. Giả sử M, N là các điểm biểu diễn hình học của $z_1$ và $z_2$ trên mặt phẳng phức. Khi đó độ dài của MN là:

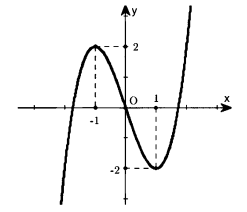
Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số sau.

Trong không gian Oxyz, cho hai điểm A (1;2;4), B (0;0;1) và mặt cầu $\left(S\right):\hspace{0.17em}{\left(x+1\right)}^2+{\left(y-1\right)}^2+z^2=4$. Mặt phẳng $\left(P\right): ax+by+cz+3=0$ đi qua A, B và cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính $T=a+b+c$

Một vật chuyển động theo quy luật $S=-\frac{1}{3}{t}^3+6t^2$ với t(s) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và S(m) là quảng đường vật duy chuyển được trong khoảng thời gian đó. Hỏi trong khoảng 9 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?

Cho phương trình $m.2^{x^2-5x+6}+2^{1-x^2}=2.2^{6-5x}$. Tìm tất cả các giá trị thực của tham số m để phương trình có 4 nghiệm phân biệt.

Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình $2\sin 2x - 2\cos 2x =\sqrt{2}$ bằng:

Đồ thị hàm số $y=3x^4-4x^3-6x^2+12x+1$ đạt cực tiểu tại điểm $M\left(x_1;y_1\right)$. Tính tổng của $T=x_1+y_1$

Đạo hàm của hàm số $y=\left(2x+1\right)\ln \left(1-x\right)$ là

Cho hàm số $y=\frac{\ln \left(2x-a\right)-2m}{\ln \left(2x-a\right)+2}$ (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức

${\log }_2\left(x^2+a^2\right)+{\log }_{\sqrt{2}}\left(x^2+a^2\right)+{\log }_{\sqrt{\sqrt{2}}}\left(x^2+a^2\right)+...+{\log }_{\underset{n căn}{\underset{⏝}{\sqrt{\sqrt{...\sqrt{2}}}}}}\left(x^2+a^2\right)-\left(2^{n+1}-1\right)\left({\log }_{2}xa+1\right)=0$ (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn $\underset{\left[1;e^2\right]}{Max}y=1$. Số phần tử của S là:/

Rút gọn biểu thức $P=\frac{a^{\sqrt{7}+1}.a^{2-\sqrt{7}}}{{\left(a^{\sqrt{2}-2}\right)}^{\sqrt{2}+2}}$, với a > 0 ta được