Tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 11 cm.

    a) Tính $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AC}}$ và chứng tỏ rằng tam giác ABC có góc A tù.

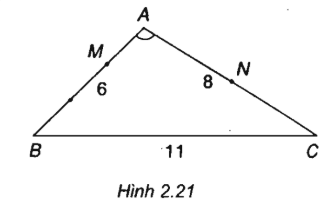
    b) Trên cạnh AB lấy điểm M sao cho AM = 2 cm và gọi N là trung điểm của cạnh AC. Tính $\overrightarrow{\mathrm{AM}}.\overrightarrow{\mathrm{AN}}$

Cho hai véc tơ $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{b}} \mathrm{có} \left|\overrightarrow{\mathrm{a}}\right|=5,\left|\overrightarrow{\mathrm{b}}\right|=12 \mathrm{và} \left|\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}\right|=13$ . Tính tích vô hướng $\overrightarrow{\mathrm{a}}. (\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}})$ và suy ra góc giữa hai vec tơ $\overrightarrow{\mathrm{a}} \mathrm{và} \overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}$

Cho hai vectơ a và vectơ b đều khác vectơ 0. Tích vô hướng $\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}$ khi nào dương, khi nào âm và khi nào bằng 0

Cho tam giác ABC. Gọi H là trực tâm của tam giác và M là trung điểm của cạnh BC. Chứng minh rằng

$\overrightarrow{\mathrm{MH}}.\overrightarrow{\mathrm{MA}}=\frac{1}{4}{\mathrm{BC}}^2$

Cho tam giác ABC có AB = 5 cm, BC = 7 cm, CA = 8 cm.

    a) Tính $\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AC}}$ rồi suy ra giá trị của góc A;

    b) Tính $\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{CB}}$

Trong mặt phẳng Oxy cho ba điểm A(-1; -1), B(3; 1) và C(6; 0).

    a) Chứng minh ba điểm A, B, C không thẳng hàng.

    b) Tính góc B của tam giác ABC.

Trong mặt phẳng Oxy cho hai điểm A(5;4) và B(3;-2). Một điểm M di động trên trục hoành Ox. Tìm giá trị nhỏ nhất của $\left|\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}\right|$

Cho tam giác đều ABC cạnh a. Tính:

$\overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AC}} \mathrm{và} \overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{BC}}$

Trong mặt phẳng Oxy cho tam giác ABC với A = (2;4), B = ( - 3;1) và C = (3;1). Tính:

    a) Tọa độ điểm D để tứ giác ABCD là hình bình hành;

    b) Tọa độ chân của đường cao vẽ từ đỉnh A.

Trong mặt phẳng Oxy, cho tam giác ABC có A = (-1; 1), B = (1; 3) và C = (1; -1)

Chứng minh tam giác ABC là tam giác vuông cân tại A.

Trong mặt phẳng Oxy cho bốn điểm A(3; 4), B(4; 1), C(2; -3), D(-1; 6). Chứng minh tứ giác ABCD nội tiếp được trong một đường tròn.

Tam giác ABC vuông tại A và có AB = AC = a. Tính:

$$\begin{gathered} \mathrm{a}) \overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{AC}} \\ \mathrm{b}) \overrightarrow{\mathrm{BA}}.\overrightarrow{\mathrm{BC}} \\ \mathrm{c}) \overrightarrow{\mathrm{AB}}.\overrightarrow{\mathrm{BC}} \end{gathered}$$

Trong mặt phẳng Oxy cho bốn điểm A(-1; 1), B(0; 2), C(3; 1) và D(0; -2). Chứng minh rằng tứ giác ABCD là hình thang cân.

Cho tam giác ABC cân (AB = AC). Gọi H là trung điểm của cạnh BC, D là hình chiếu vuông góc của H trên cạnh AC, M là trung điểm của đoạn HD. Chứng minh rằng AM vuông góc với BD.

Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau và cắt nhau tại M. Gọi P là trung điểm của cạnh AD. Chứng minh rằng MP vuông góc với BC khi và chỉ khi $\overrightarrow{\mathrm{MA}}.\overrightarrow{\mathrm{MC}}=\overrightarrow{\mathrm{MB}}.\overrightarrow{\mathrm{MD}}$

Áp dụng tính chất giao hoán và tính chất phân phối của tích vô hướng hãy chứng minh các kết quả sau đây:

$$\begin{gathered} {(\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}})}^2 = {\left|\overrightarrow{\mathrm{a}}\right|}^2+{\left|\overrightarrow{\mathrm{b}}\right|}^2+2\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}} \\ {(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}})}^2 = {\left|\overrightarrow{\mathrm{a}}\right|}^2+{\left|\overrightarrow{\mathrm{b}}\right|}^2-2\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}} \\ (\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}})(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}})= {\left|\overrightarrow{\mathrm{a}}\right|}^2-{\left|\overrightarrow{\mathrm{b}}\right|}^2 \end{gathered}$$