Điểm nào sau đây thuộc đồ thị hàm số \[y = \frac{{2x - 1}}{{x\left( {3x - 4} \right)}}\]?
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Ta đặt \[f\left( x \right) = \frac{{2x - 1}}{{x\left( {3x - 4} \right)}}\].
Biểu thức f(x) có nghĩa khi và chỉ khi x(3x – 4) ≠ 0.
Tức là khi x ≠ 0 và 3x – 4 ≠ 0.
Do đó x ≠ 0 và \(x \ne \frac{4}{3}\).
Vì vậy hàm số có tập xác định là \(D = \mathbb{R}\backslash \left\{ {0;\frac{4}{3}} \right\}\).
Các điểm M, P có hoành độ lần lượt là 0 và \(\frac{4}{3}\) đều không thuộc tập xác định D của hàm số đã cho.
Do đó ta loại phương án A, C.
⦁ Ta xét điểm \(N\left( {2; - \frac{3}{4}} \right)\), ta có hoành độ 2 ∈ D.
Ta có \[f\left( 2 \right) = \frac{{2.2 - 1}}{{2\left( {3.2 - 4} \right)}} = \frac{3}{4} \ne - \frac{3}{4}\].
Do đó điểm \(N\left( {2; - \frac{3}{4}} \right)\) không thuộc đồ thị hàm số \[y = \frac{{2x - 1}}{{x\left( {3x - 4} \right)}}\].
Vì vậy ta loại phương án B.
⦁ Ta xét điểm \(Q\left( { - 2; - \frac{1}{4}} \right)\), ta có –2 ∈ D.
Ta có \[f\left( { - 2} \right) = \frac{{2.\left( { - 2} \right) - 1}}{{ - 2\left[ {3.\left( { - 2} \right) - 4} \right]}} = - \frac{1}{4}\].
Do đó điểm \(Q\left( { - 2; - \frac{1}{4}} \right)\) thuộc đồ thị hàm số \[y = \frac{{2x - 1}}{{x\left( {3x - 4} \right)}}\].
Vậy ta chọn phương án D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hàm số y = f(x) có đồ thị như hình vẽ bên.
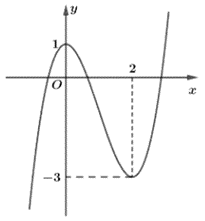
Khẳng định nào sau đây đúng?
Xét tính đồng biến, nghịch biến của hàm số \(y = \sqrt[3]{x} + 3\).