Cặp đường thẳng nào sau đây vuông góc với nhau?

Một gương có mặt cắt là một hypebol có phương trình $\frac{x^2}{144}-\frac{y^2}{16}=1$  được dùng để chụp ảnh toàn cảnh. Máy ảnh hướng về phía đỉnh của gương và được đặt ở vị trí sao cho ống kính trùng với một tiêu điểm của gương như hình vẽ.

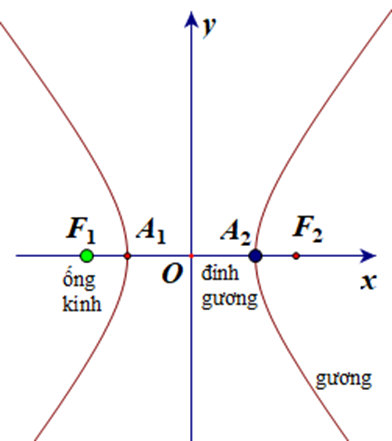
Biết rằng x, y được đo theo inch. Khoảng cách từ ống kính tới đỉnh gương bằng khoảng:

Đường thẳng ∆ đi qua giao điểm của hai đường thẳng d₁: 2x + y – 3 = 0 và d₂: x – 2y + 1 = 0, đồng thời tạo với d₃: y – 1 = 0 một góc $\frac{\pi }{4}.$  Phương trình đường thẳng ∆ là:

Một anten gương đơn hình parabol có phương trình y² = 20x. Ống thu của anten được đặt tại tiêu điểm của nó. Ta sẽ đặt ống thu tại điểm có tọa độ là:

Cho M(x; y) nằm trên elip (E): $\frac{x^2}{121}+\frac{y^2}{81}=1$ . Tỉ số giữa tiêu cự và độ dài trục lớn bằng:

Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng  là:

Đường tròn (C) có tâm I(–2; 3) và đi qua điểm M(2; –3) có phương trình là:

Cho ∆ABC có A(2; –1), B(4; 5), C(–3; 2). Phương trình tổng quát của đường trung tuyến AM là:

Tọa độ tâm I của đường tròn đi qua ba điểm A(0; 4), B(2; 4), C(4; 0) là:

Giao điểm M của hai đường thẳng (d): $\{\begin{array}{l}x=1-2t\\ y=-3+5t\end{array}$  và (d’): 3x – 2y – 1 = 0 là:

Trong mặt phẳng Oxy, cho hai điểm A(2; 4) và B(–2; 10). Giá trị k để điểm D(k; k + 1) thuộc đường thẳng AB là:

Trong mặt phẳng Oxy, cho đường thẳng d: x + 2y – 3 = 0 và hai điểm A(–1; 2). B(2; 1). Điểm C thuộc đường thẳng d sao cho diện tích ∆ABC bằng 2. Tọa độ điểm C là:

Cho $\overrightarrow{a}=(1;2), \overrightarrow{b}=(-2;3)$. Góc giữa hai vectơ $\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}$và $\overrightarrow{v}=\overrightarrow{a}-5\overrightarrow{b}$   bằng

Cho phương trình x² + y² – 2mx – 4(m – 2)y + 6 – m = 0. Điều kiện của m để phương trình đã cho là một phương trình đường tròn là:

Trong mặt phẳng Oxy, cho ∆ABC có A(–4; 1), B(2; 4), C(2; –2). Tọa độ trọng tâm I của ∆ABC là:

Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là: