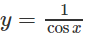Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [2;4]

(Đề thi tốt nghiệp THPT năm 2008)

Giá trị lớn nhất của hàm số y = -x2 + 4x - 5 trên đoạn [0;3] bằng:

Một chất điểm chuyển động theo quy luật s = 6t2 – t3. Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.

Tìm các giá trị của m để phương trình : x3 – 3x2 – m = 0 có ba nghiệm phân biệt.

Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0).

Cho số dương m. Hãy phân tích m thành tổng của hai số dương sao cho tích của chúng là lớn nhất.

Giá trị nhỏ nhất của hàm số sau trên khoảng (0; $\frac{\mathrm{\pi }}{2}$) là:

Giá trị nhỏ nhất của hàm số f(x) = x3 + 3x2 - 9x - 7 trên đoạn [-4;3] bằng:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) f(x) = √(25−x2) trên đoạn [-4; 4]

b) f(x) = |x2 – 3x + 2| trên đoạn [-10; 10]

c) f(x) = $\frac{1}{\mathrm{sinx}}$ trên đoạn [$\frac{\mathrm{\pi }}{3}$; $\frac{5\mathrm{\pi }}{6}$]

d) f(x) = 2sinx + sin2x trên đoạn [0; $\frac{3\mathrm{\pi }}{2}$]

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [0;2] bằng

Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) 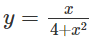 trên khoảng (−∞;+∞);

b)  trên khoảng 

Giá trị lớn nhất của hàm số sau trên khoảng (-∞; +∞) là: