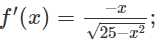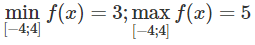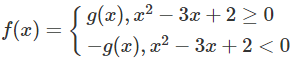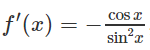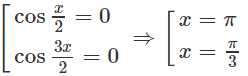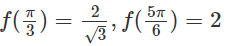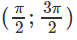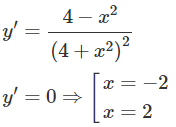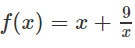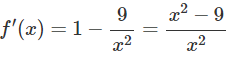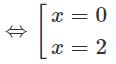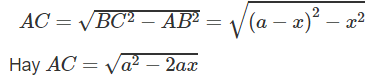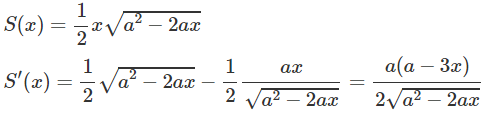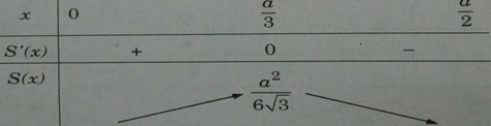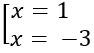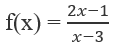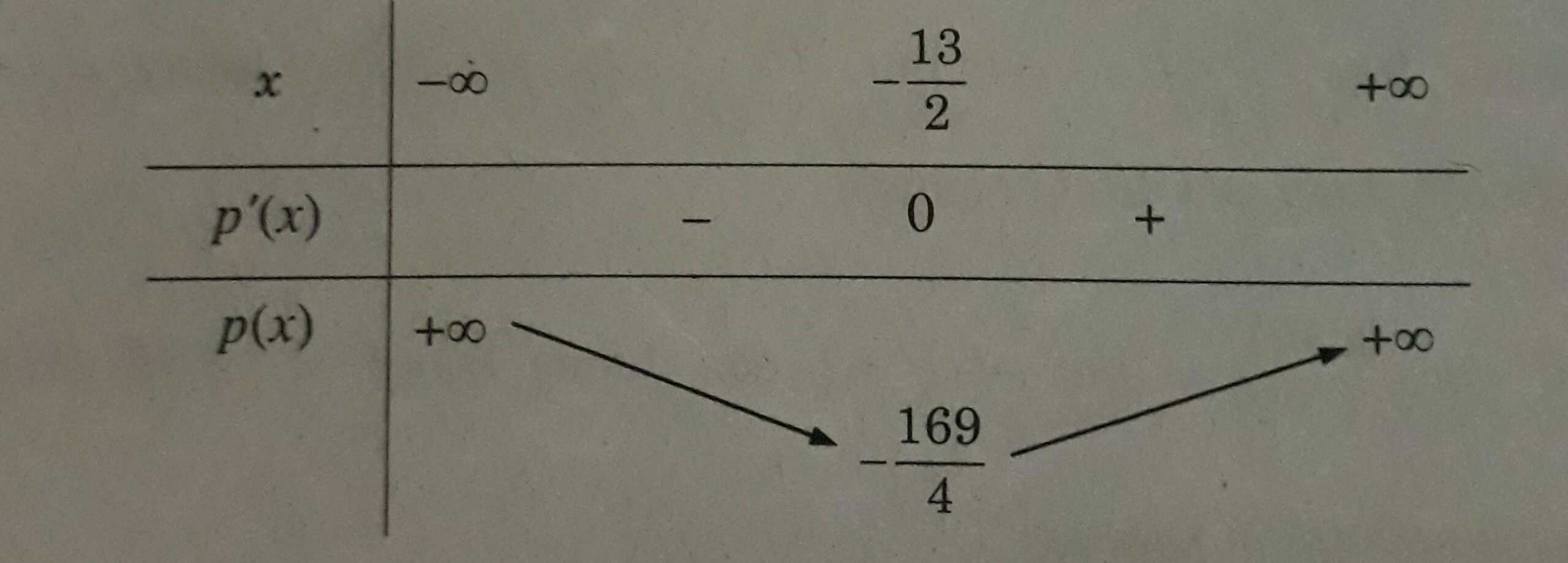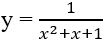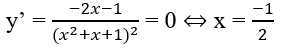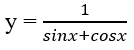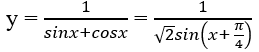13 câu hỏi trắc nghiệm thuộc Giải sbt Giải tích 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Giải SBT Toán 12 Giải tích - Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Giải sbt Giải tích 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

1085 lượt thi
13 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) f(x) = √(25−x2) trên đoạn [-4; 4]

b) f(x) = |x2 – 3x + 2| trên đoạn [-10; 10]

c) f(x) = $\frac{1}{sinx}$ trên đoạn [ $\frac{π}{3}$ ; $\frac{5 π}{6}$ ]

d) f(x) = 2sinx + sin2x trên đoạn [0; $\frac{3 π}{2}$ ]

Xem đáp án

f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).

Hàm số đạt cực đại tại x = 0 và fCĐ = 5

Mặt khác, ta có f(-4) = f(4) = 3

Vậy

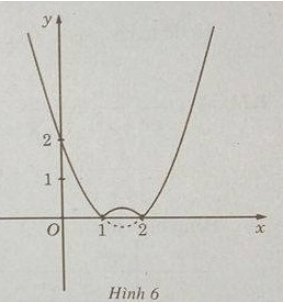
d) f(x) = |x2 − 3x + 2| trên đoạn [-10; 10]

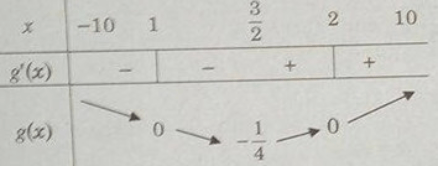
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x2 – 3x + 2.

Ta có:

g′(x) = 2x − 3; g′(x) = 0 ⇔ x = $\frac{3}{2}$

Bảng biến thiên:

Vì

nên ta có đồ thị f(x) như sau:

Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132

f′(x) < 0 nên và f’(x) > 0 trên ( $\frac{π}{2}$ ; $\frac{5 π}{6}$ ] nên hàm số đạt cực tiểu tại x = $\frac{π}{2}$ và

fCT = f( $\frac{π}{2}$ ) = 1

Mặt khác, f( $\frac{π}{3}$ ) = 2√3, f( $\frac{5 π}{6}$ ) = 2

Vậy min f(x) = 1; max f(x) = 2

g) f(x) = 2sinx + sin2x trên đoạn [0; $\frac{3 π}{2}$ ]

f′(x) = 2cosx + 2cos2x = 4cos( $\frac{x}{2}$ ).cos3( $\frac{x}{2}$ )

f′(x) = 0

⇔

Ta có: f(0) = 0,

Từ đó ta có: min f(x) = −2 ; max f(x) = $\frac{3 \sqrt{3}}{2}$

Câu 2:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) 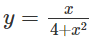trên khoảng (−∞;+∞);

b) 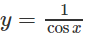trên khoảng

Xem đáp án

a) 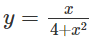trên khoảng (−∞;+∞);

Từ đó ta có min f(x) = −1/4; max f(x) = 1/4

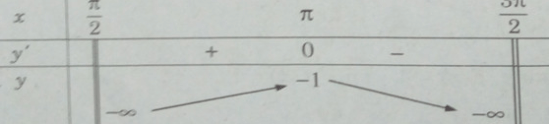
b) 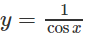trên khoảng

y′ = 0 ⇔ x = π

Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là:

max y = y(π) = −1.

Câu 3:

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [2;4]

(Đề thi tốt nghiệp THPT năm 2008)

Xem đáp án

TXĐ: D = R\{0}

f′(x) = 0 ⇔ x = 3 hoặc x = -3

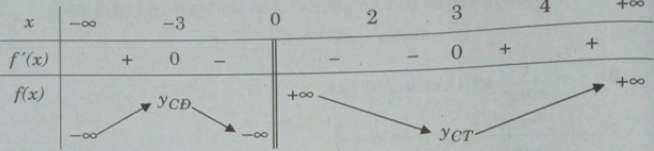
Hàm số nghịch biến trong các khoảng (-3;0), (0;3) và đồng biến trong các khoảng (−∞;3), (3;+∞)

Bảng biến thiên:

Ta có: [2;4] ⊂ (0; +∞); f(2) = 6,5; f(3) = 6; f(4) = 6,25

Suy ra

min f(x) = f(3) = 6; max f(x) = f(2) = 6,5

Câu 4:

Tìm các giá trị của m để phương trình : x3 – 3x2 – m = 0 có ba nghiệm phân biệt.

Xem đáp án

Đặt f(x) = x3 – 3x2 (C1)

y = m (C2)

Phương trình x3 – 3x2 – m = 0 có ba nghiệm phân biệt khi và chỉ khi (C1) và (C2) có ba giao điểm.

Ta có:

f′(x) = 3x2 − 6x = 3x(x − 2) = 0

Bảng biến thiên:

Suy ra (C1), (C2) cắt nhau tại 3 điểm khi -4 < m < 0

Kết luận : Phương trình x3 – 3x2 – m = 0 có ba nghiệm phân biệt với những giá trị của m thỏa mãn điều kiện: -4 < m < 0.

Câu 5:

Cho số dương m. Hãy phân tích m thành tổng của hai số dương sao cho tích của chúng là lớn nhất.

Xem đáp án

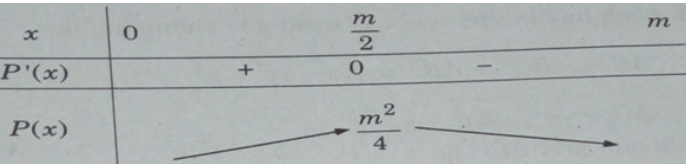
Cho m > 0. Đặt x là số thứ nhất, 0 < x < m , số thứ hai là m – x

Xét tích P(x) = x(m – x)

Ta có: P’(x) = -2x + m

P′(x) = 0 ⇔ x = $\frac{m}{2}$

Bảng biến thiên

Từ đó ta có giá trị lớn nhất của tích hai số là: max P(x) = P( $\frac{m}{2}$ ) = $\frac{m^{2}}{4}$

Câu 6:

Một chất điểm chuyển động theo quy luật s = 6t2 – t3. Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.

Xem đáp án

S = 6t2 − t3, t > 0

Vận tốc chuyển động là v = s’ , tức là v = 12t – 3t2

Ta có: v’ = 12 – 6t

v’ = 0 ⇔ t = 2

Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+∞).

Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó max V = VCD = v(2) = 12(m/s).

Câu 7:

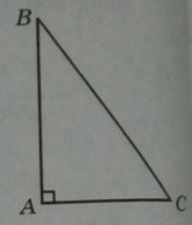
Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0).

Xem đáp án

Kí hiệu cạnh góc vuông AB là x, 0 < x < $\frac{a}{2}$

Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là:

Diện tích tam giác ABC là:

S′(x) = 0 ⇔ x = $\frac{a}{3}$

Bảng biến thiên:

Tam giác có diện tích lớn nhất khi AB = $\frac{a}{3}$ ; BC = $\frac{2 a}{3}$

Câu 8:

Giá trị lớn nhất của hàm số y = -x2 + 4x - 5 trên đoạn [0;3] bằng:

A. -1

B. 1

C. 2

D. 0

Xem đáp án

Đáp án: A.

Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2

⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.

Cách khác: Vì a = -1 nên parabol y = -x2 + 4x - 5 đạt cực đạt tại đỉnh (2; -1). Vì vậy giá trị lớn nhất của hàm số trên đoạn [0;3] là y(2) = -1.

Câu 9:

Giá trị nhỏ nhất của hàm số f(x) = x3 + 3x2 - 9x - 7 trên đoạn [-4;3] bằng:

A. -5

B. 0

C. 7

D. -12

Xem đáp án

Đáp án: D.

Ta có f(x) = x3 + 3x2 - 9x - 7 ⇒ f'(x) = 3x2 + 6x - 9 = 0

⇔

f(-4) = 13, f(-3) = 30, f(1) = -12, f(3) = 20

Vậy min f(x) = -12.

Câu 10:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [0;2] bằng

A. $\frac{1}{3}$ và -3

B. $\frac{3}{2}$ và -1

C. 2 và -3

D. $\frac{1}{2}$ và 5

Xem đáp án

Đáp án: A.

Tập xác định: D = R \{3}

∀x ∈ D.

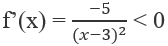
Do đó f(x) nghịch biến trên (-∞; 3) và (3; +∞).

Ta thấy [0;2] ⊂ (-∞;3). Vì vậy

max f(x) = f(0) = 1/3, min f(x) = f(2) = -3.

Câu 11:

Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất

A. 13 và 0

B. $\frac{13}{2}$ và $- \frac{13}{2}$

C. 15 và 2

D. 30 và 15

Xem đáp án

Đáp án: B.

Gọi một trong hai số phải tìm là x, ta có số kia là x + 13

Xét tích p(x) = x(x + 13) = x2 + 13x;

p'(x) = 2x + 13; p'(x) = 0 ⇔ x = $- \frac{13}{2}$ .

Bảng biến thiên

Vậy tích hai số là bé nhất khi một số là x = $- \frac{13}{2}$ và số kia là x + 13 = $\frac{13}{2}$ .

Câu 12:

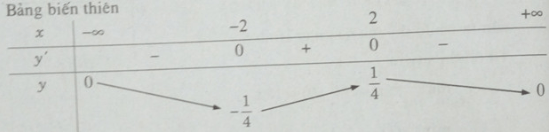
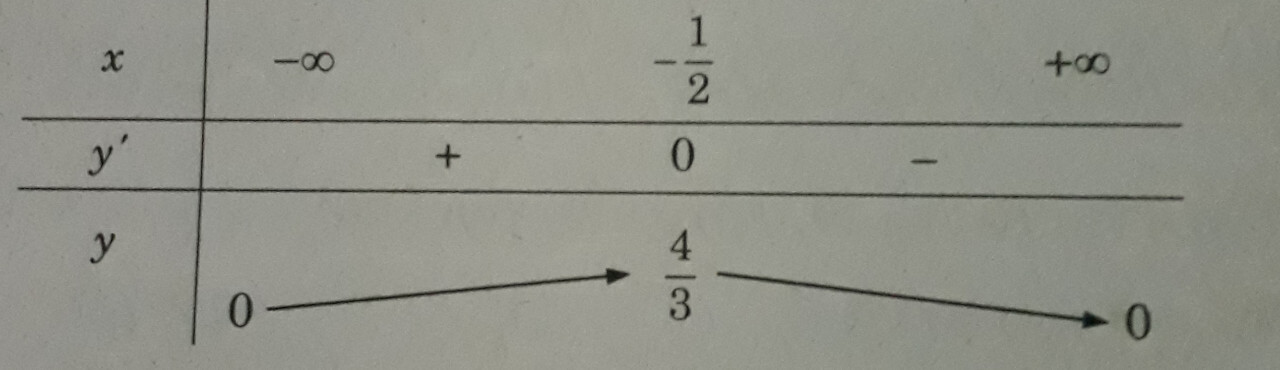
Giá trị lớn nhất của hàm số sau trên khoảng (-∞; +∞) là:

A. 1

B. $\frac{4}{3}$

C. $\frac{5}{3}$

D. 0

Xem đáp án

Đáp án: B.

Bảng biến thiên

max y = $\frac{4}{3}$ .

Câu 13:

Giá trị nhỏ nhất của hàm số sau trên khoảng (0; $\frac{π}{2}$ ) là:

A. 1

B. 2√2

C. -√2

D. 2√/2

Xem đáp án

Đáp án: D.

Trên khoảng (0; π/2), sin(x + π/4) ≤ 1;

Dấu "=" xảy ra ⇔ x = $\frac{π}{4}$

Suy ra giá trị nhỏ nhất của hàm số là min y = y( $\frac{π}{4}$ ) = $\frac{\sqrt{2}}{2}$ .

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 12 Giải tích - Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Giải sbt Giải tích 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Danh sách câu hỏi

Bài thi liên quan