Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:

a) y² = 12x;                       

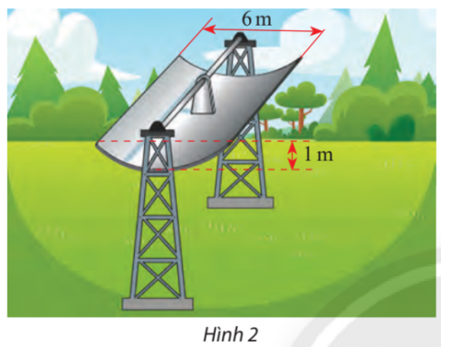
Cổng chào của một thành phố có dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (Hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc vẽ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng.

d) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 8.

c) Đi qua hai điểm A(4; 1), B(6; 5) và có tâm nằm trên đường thẳng 4x + y – 16 = 0;

d) Đi qua gốc tọa độ và cắt hai trục tọa độ tại các điểm có hoành độ là a, tung độ là b.

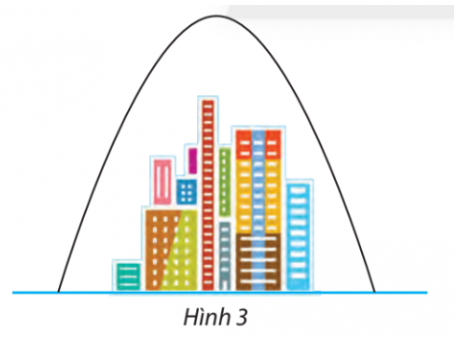
Một gương lõm có mặt cắt hình parabol như Hình 1, có tiêu điểm cách đỉnh 5 cm. Cho biết bề sâu của gương là 45 cm, tính khoảng cách AB.

b) Tính khoảng cách từ tâm đường ống đến đỉnh của parabol.

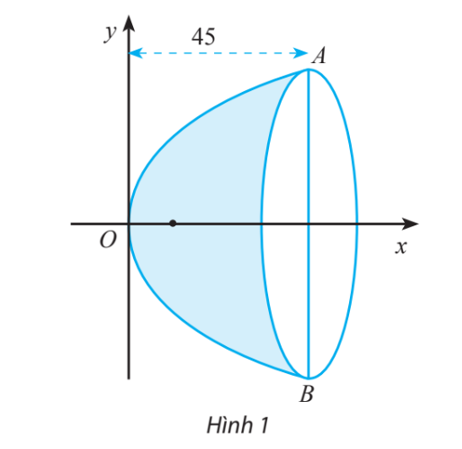
Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol (Hình 2). Nước sẽ chảy thông qua một dường ống nằm ở tiêu điểm của parabol.

a) Viết phương trình chính tắc của parabol.

Viết phương trình chính tắc của parabol thỏa mãn từng điều kiện sau:

a) Tiêu điểm (4; 0);

Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2).

a) Chứng minh ABCD là hình vuông. 

Viết phương trình tiếp tuyến của đường tròn (C): (x − 5)² + (y − 3)² = 100 tại điểm M(11; 11).

Tính khoảng cách giữa hai đường thẳng: Δ: 6x + 8y – 13 = 0 và Δ′: 3x + 4y – 27 = 0.

Viết phương trình chính tắc của elip thỏa mãn từng điều kiện:

a) Đỉnh (5; 0), (0; 4);

a) Có tâm I(−2; 4) và bán kính bằng 9;

b) Đỉnh (5; 0), tiêu điểm (3; 0);

Tính bán kính của đường tròn tâm M(−2; 3) và tiếp xúc với đường thẳng d: 14x − 5y + 60 = 0.