Giải bài tập Toán 7 Bài tập cuối chương 3 trang 59

Video giải bài tập Toán 7 Bài tập cuối chương 3 trang 59

Bài 3.32 trang 59 Toán 7 Tập 1: Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A vuông góc với d, tức là nếu có hai đường thẳng đi qua A vuông góc với d thì chúng phải trùng nhau.

Lời giải:

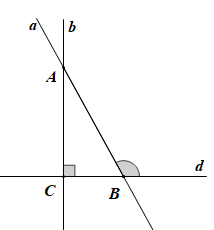
Chứng minh (Hình vẽ trên):

Theo giả thiết ta có $a\perp d$ tại B nên $\widehat{ABd}=90°$; $b\perp d$ tại C nên $\widehat{ACd}=90°.$ 

 Do đó $\widehat{ABd}=\widehat{ACd}=90°.$

Mà hai góc này ở vị trí đồng vị nên a // b (dấu hiệu nhận biết hai đường thẳng song song).

Do hai đường thẳng a và b cùng đi qua A mà a // b nên hai đường thẳng này trùng nhau.

Vậy a ≡ b. 

Bài 3.33 trang 59 Toán 7 Tập 1: Vẽ ba đường thẳng phân biệt a, b, c sao cho a // b, b // c và hai đường thẳng phân biệt m, n cùng vuông góc với a. Hỏi trên hình có bao nhiêu cặp đường thẳng song song, có bao nhiêu cặp đường thẳng vuông góc?

Lời giải:

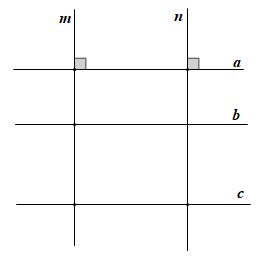
Áp dụng các tính chất của hai đường thẳng song song, ta có:

Vì a // b, b // c nên a // c. 

Do m ⊥ a, n ⊥ a nên m // n. 

Ta có: a // b, m ⊥ a nên m ⊥ b.

Có a // c, m ⊥ a nên m ⊥ c.

Vì a // b, n ⊥ a nên n ⊥ b. 

Lại có a // c, n ⊥ a nên n ⊥ c.

Vậy:

Trên hình vẽ trên có 4 cặp đường thẳng song song là: a // b; b // c; a // c; m // n.

Trên hình vẽ trên có 6 cặp đường thẳng vuông góc là: $m\perp a,$ $m\perp b,$ $m\perp c,$ $n\perp a,$ $n\perp b,$ $n\perp c.$ 

Bài 3.34 trang 59 Toán 7 Tập 1: Cho Hình 3.50, trong đó hai tia Ax, By nằm trên hai đường thẳng song song. Chứng minh rằng $\widehat{C}=\widehat{A}+\widehat{B}.$

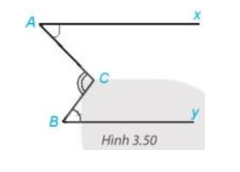
Lời giải:

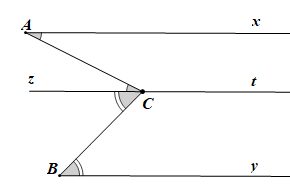
Chứng minh (Hình vẽ trên):

Theo giả thiết Ax và By nằm trên hai đường thẳng song song nên Ax // By.

Qua C vẽ đường thẳng zt song song với đường thẳng chứa tia Ax.

Khi đó zt // By (hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau).

Từ zt // Ax ta có $\widehat{xAC}=\widehat{ACz}$ (hai góc so le trong).

Từ zt // By ta có $\widehat{zCB}=\widehat{CBy}$ (hai góc so le trong).

Suy ra $\widehat{ACB}=\widehat{ACz}+\widehat{zCB}=\widehat{xAC}+\widehat{CBy}.$  (điều phải chứng minh)

Vậy $\widehat{ACB}=\widehat{xAC}+\widehat{CBy}.$

Bài 3.35 trang 59 Toán 7 Tập 1: Cho Hình 3.51, trong đó Ox và Ox' là hai tia đối nhau.

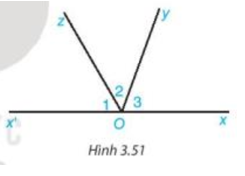
a) Tính tổng số đo ba góc O₁, O₂, O₃.

Gợi ý: $\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=\left(\widehat{O_1}+\widehat{O_2}\right)+\widehat{O_3},$ trong đó $\widehat{O_1}+\widehat{O_2}=\widehat{x^{\text{'}}Oy}.$

$\widehat{x^{\text{'}}Oy},\widehat{yOx}$ là hai góc kề bù.

b) Cho $\widehat{O_1}=60°,\widehat{O_3}=70°.$ Tính $\widehat{O_2}.$

Lời giải:

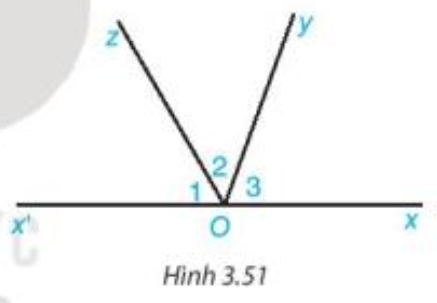
Chứng minh (Hình vẽ trên):

a) Theo giả thiết ta có Ox và $O{x}^{\text{'}}$ là hai tia đối nhau nên $\widehat{x^{\text{'}}Oy},\widehat{yOx}$ là hai góc kề bù.

Suy ra $\widehat{x^{\text{'}}Oy}+\widehat{yOx}=180°$ (tính chất hai góc kề bù).

Hay $\widehat{x^{\text{'}}Oy}+\widehat{O_3}=180°.$ 

Trong hình vẽ trên, tia Oz nằm giữa hai tia $O{x}^{\text{'}}$ và tia Oy nên $\widehat{x^{\text{'}}Oy}=\widehat{x^{\text{'}}\text{Oz}}+\widehat{zOy}$ hay $\widehat{x^{\text{'}}Oy}=\widehat{O_1}+\widehat{O_2}.$ 

Do đó từ $\widehat{x^{\text{'}}Oy}+\widehat{O_3}=180°$ suy ra $\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=180°.$

Vậy $\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=180°.$

b) Theo câu a ta có $\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=180°.$

Suy ra $\widehat{O_2}=180°-\widehat{O_1}-\widehat{O_3}.$ 

Mà $\widehat{O_1}=60°,\widehat{O_3}=70°.$

Do đó $\widehat{O_2}=180°-60°-70°.$ 

$\widehat{O_2}=120°-70°$ 

$\widehat{O_2}=50°.$ 

Vậy $\widehat{O_2}=50°.$ 

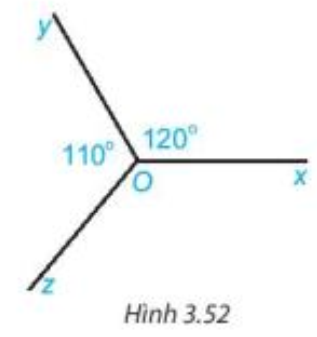
Bài 3.36 trang 59 Toán 7 Tập 1: Cho Hình 3.52, biết $\widehat{xOy}=120°,\widehat{y\text{O}z}=110°.$ Tính số đo góc zOx.

(Gợi ý: Kẻ thêm tia đối của tia Oy).

Lời giải:

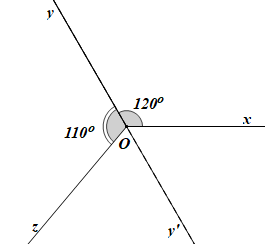
Chứng minh (Hình vẽ trên):

Kẻ tia Oy' là tia đối của tia Oy.

+) Góc y'Ox và góc xOy là hai góc kề bù nên $\widehat{y^{\text{'}}Ox}+\widehat{xOy}=180°$ (tính chất hai góc kề bù).

Suy ra $\widehat{y^{\text{'}}Ox}=180°-\widehat{xOy}$

$\widehat{y^{\text{'}}Ox}=180°-120°$ 

$\widehat{y^{\text{'}}Ox}=60°$

+) Góc yOz và góc zOy' là hai góc kề bù nên $\widehat{yOz}+\widehat{zO{y}^{\text{'}}}=180°$ (tính chất hai góc kề bù).

Suy ra $\widehat{zO{y}^{\text{'}}}=180°-\widehat{yOz}$

$\widehat{zO{y}^{\text{'}}}=180°-110°$ 

$\widehat{zO{y}^{\text{'}}}=70°$

+) Tia Oy' nằm giữa hai tia Ox và Oz nên $\widehat{zOx}=\widehat{zO{y}^{\text{'}}}+\widehat{y^{\text{'}}\text{Ox}}.$ 

Mà $\widehat{zO{y}^{\text{'}}}=70°$ và $\widehat{y^{\text{'}}Ox}=60°.$

Suy ra $\widehat{zOx}=70°+60°$ 

$\widehat{zOx}=130°.$ 

Vậy $\widehat{zOx}=130°.$