Một người bán gà lần thứ nhất bán $\frac{4}{9}$  số gà lần thứ 2 bán $\frac{3}{5}$  số gà còn lại, như thế, lần thứ nhất bán nhiều hơn lần thứ hai 4 con. Hỏi người đó bán tất cả bao nhiêu con gà ?

Có bao nhiêu số nguyên là tổng của ba phần tử phân biệt của tập hợp {1; 4; 7; 10; 13; 16; 19}.

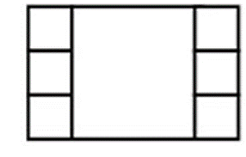
Hình chữ nhật dưới đây được cắt thành 7 hình vuông. Biết chu vi của hình chữ nhật là 160 cm, tính diện tích của hình vuông lớn.

Cho tam giác ABC vuông tại A, $\widehat{ACB}=30°$ . Tia phân giác của $\widehat{ABC}$  cắt cạnh AC tại M. Lấy K trên cạnh BC sao cho BK = BA.

a) Chứng minh tam giác ABM và tam giác KBM.

Một cái thùng hình hộp chữ nhật có chiều dài 12dm, chiều rộng 9dm, chiều cao 6dm. Người ta xếp vào đó các khối hình lập phương bằng nhau, sao cho vừa đầy khít thùng. Tính số khối lập phương có thể xếp được như vậy.

Số nguyên tố nhỏ hơn 1000000 là số bao nhiêu ?

Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau. Điểm E thuộc OC, nối AE cắt (O) tại M.

a) Chứng minh tứ giác OBME nội tiếp.

Nếu tăng chiều dài hình chữ nhật thêm 10% và giảm chiều rộng đi 10% thì diện tích của hình chữ nhật sẽ thay đổi như thế nào ?

Cho đường tròn (O; R) và điểm A nằm bên ngoài đường tròn. Kẻ tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

1. Chứng minh ABOC là tứ giác nội tiếp.

Hai số có tổng là 346. Biết số bé là số có hai chữ số và khi viết thêm chữ số 2 vào trước số bé thì được số lớn.Tìm số lớn.

Chứng tỏ rằng các tổng, hiệu sau không chia hết cho 10.

a) A= 98 × 96 × 94 × 92 – 91 × 93 × 95 × 97.

Cho dãy số: 2; 6; 12; 20;.... Tìm số hạng tiếp theo của dãy.

Số hạng tiếp theo của dãy số sau: 2, 3, 5, 9, 17..., là ?

Một thửa ruộng hình chữ nhật có chiều dài hơn chiều rộng 30 m và chiều rộng bằng $\frac{2}{5}$  chiều dài. Trung bình cứ 1 m² thu hoạch được $\frac{3}{5}$  kg thóc. Hỏi thửa ruộng đó thu hoạch được bao nhiêu tạ thóc.

Tìm hai số có tổng là 234, biết rằng nếu lấy số thứ nhất trừ đi số thứ hai rồi cộng với hiệu của chúng thì được 172.