Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 12)
-
2063 lượt thi
-
105 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Chứng minh rằng mọi số tự nhiên có 3 chữ số giống nhau đều chia hết cho 37.
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có 3 chữ số giống nhau là . Ta có:
Mà a.37.3 chia hết cho 37
Vậy mọi tự nhiên có 3 chữ số giống nhau luôn chia hết cho 37.
Câu 2:
Có bao nhiêu số lẻ có 3 chữ số mà các chữ số khác nhau ?
 Xem đáp án
Xem đáp án
Gọi số cần tìm là
Chữ số c có 5 cách chọn (vì là số lẻ)
Chữ số a có 8 cách chọn (khác 0 và khác chữ số c)
Chữ số b có 8 cách chọn (khác chữ số a và chữ số c)
Vậy số số thỏa mãn yêu cầu đề bài là: 5.8.8 = 320 (số).
Câu 3:
Có bao nhiêu số có 2 chữ số đều chia hết cho cả 2 và 3.
 Xem đáp án
Xem đáp án
Chia hết cho cả 2 và 3 tức là chia hết cho 6.
Ta có dãy số : 12 ; 18 ... 96
Số các số chia hết cho cả 2 và 3 là
(96 – 12) : 6 + 1 = 15 số.
Câu 4:
Có bao nhiêu số lẻ có 3 chữ số mà các chữ số khác nhau ?
 Xem đáp án
Xem đáp án
Gọi số cần tìm là .
Chữ số c có 5 cách chọn (vì là số lẻ)
Chữ số a có 8 cách chọn (khác 0 và khác chữ số c)
Chữ số b có 8 cách chọn (khác chữ số a và chữ số c)
Vậy số số thỏa mãn yêu cầu đề bài là: 5.8.8 = 320 (số).
Câu 5:
Khẩu phần ăn nhẹ buổi chiều của các bé mẫu giáo là một cái bánh. Nếu trường có 537 cháu thì phải mở bao nhiêu hộp bánh,biết rằng mỗi hộp có 16 chiếc bánh?
 Xem đáp án
Xem đáp án
Ta có: 537 : 16 = 33 (dư 9)
Cần phải mở số hộp bánh là: 33 + 1 = 34 (hộp bánh).
Câu 6:
Một cái thùng hình hộp chữ nhật có chiều dài 12dm, chiều rộng 9dm, chiều cao 6dm. Người ta xếp vào đó các khối hình lập phương bằng nhau, sao cho vừa đầy khít thùng. Tính số khối lập phương có thể xếp được như vậy.
 Xem đáp án
Xem đáp án
Để có số khối lập phương xếp vừa khít thùng thì số đo các canh của hình lập phương là số tự nhiên lớn nhất mà các số 12, 9, 6 đều chia hết cho số đó.
Vì: 12 = 3.4; 9 = 3.3 và 6 =2.3
Vậy cạnh của khối lập phương là: 3 dm
Thể tích thùng là: 12.9.6 = 648 dm3.
Thể tích của hình lập phương là: 3.3.3 = 27 dm3.
Số khối lập phương ít nhất là: 648 : 27 = 24 khối.
Câu 7:
Một hình chữ nhật có chu vi 28 cm, chiều dài hơn chiều rộng 2 cm. Tìm diện tích hình chữ nhật ?
 Xem đáp án
Xem đáp án
Tổng của chiều dài và chiều rộng là:
28 : 2 = 14 (cm)
Chiều dài là:
(14 + 2) : 2 = 8 (cm)
Chiều rộng là:
(14 – 2) : 2 = 6 (cm)
Diện tích là:
8 × 6 = 48 (cm2).
Câu 8:
Một mảnh đất hình chữ nhật có chiều dài là m. Chiều rộng bằng chiều dài. Tính diện tích hình chữ nhật đó dưới dạng số thập phân.
 Xem đáp án
Xem đáp án
Chiều dài là: = 0,8 m
Chiều rộng là: (m)
Diện tích hình chữ nhật là: 0,8.0,6 = 0,48 (m2).
Câu 9:
Một thửa ruộng hình chữ nhật có chiều dài hơn chiều rộng 30 m và chiều rộng bằng chiều dài. Trung bình cứ 1 m2 thu hoạch được kg thóc. Hỏi thửa ruộng đó thu hoạch được bao nhiêu tạ thóc.
 Xem đáp án
Xem đáp án
Hiệu số phần bằng nhau là: 5 – 2 = 3
Chiều dài thửa ruộng là: 30 : 3 × 5 = 50 (m)
Chiều rộng thửa ruộng là: 30 : 3 × 2 = 20 (m)
Diện tích thửa ruộng là: 50 × 20 = 1000 (m2)
Thửa ruộng đó thu hoạch được số ki–lo–gam thóc là:
(kg) = 6 (tạ)
Đáp số: 6 tạ thóc.
Câu 10:
Người ta dùng các tấm nhựa xốp hình vuông cạnh 30 cm để trải kín nên một căn phòng hình chữ nhật có chiều dài là 6 m và chiều rộng 4 m 5 dm. Biết rằng mỗi tấm đó giá 2000 đồng. Hỏi phải tốn bao nhiêu nhiều tiền để mua đủ các tấm nhựa xốp đó ?
 Xem đáp án
Xem đáp án
Đổi: 6 m = 600 cm; 4 m 5 dm = 450 cm
Diện tích căn phòng là:
600 × 450 = 270000 (cm2)
Diện tích một tấm xốp là:
30 × 30 = 900 (cm2)
Số tấm xốp cần dùng là:
270000 : 900 = 300 (tấm)
Số tiền cần dùng là:
300 × 2000 = 600000 (đồng)
Đáp số: 600 000 đồng.
Câu 11:
. Người ta muốn chia 374 quyển vở, 68 thước kẻ va 340 nhãn vở thành một số phần thưởng như nhau. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng, mỗi phần thưởng có bao nhiêu quyển vở, thước kẻ, nhãn vở ?
 Xem đáp án
Xem đáp án
Tìm ƯCLN của cả ba loại. Ta có:
374 = 2.11.17
68 = 22.17
340 = 17. 22.5
ƯCLN(374, 68, 340) = 34.
Do đó, số phần thưởng được chia nhiều nhất là 34.
Mỗi phần có:
374 : 34 = 11 (quyển vở)
68 : 34 = 2 (thước kẻ)
340 : 34 = 10 (nhãn vở).
Câu 12:
Nếu tăng chiều dài hình chữ nhật thêm 10% và giảm chiều rộng đi 10% thì diện tích của hình chữ nhật sẽ thay đổi như thế nào ?
 Xem đáp án
Xem đáp án
Gọi chiều dài ban đầu của hình chữ nhật là 100% thì chiều dài mới là:
100% + 10% = 110% (chiều dài ban đầu)
Gọi chiều rộng ban đầu của hình chữ nhật là 100% thì chiều rộng mới là:
100% – 10% = 90% (chiều rộng ban đầu)
Vậy diện tích mới so với diện tích cũ có tỷ số là:
x = 110% . 90% = 99/100
Vậy diện tích của hình chữ nhật sẽ giảm đi số % là:
(100 – 99) : 100 = 1%.
Câu 14:
Cho dãy số: 2; 6; 12; 20;.... Tìm số hạng tiếp theo của dãy.
 Xem đáp án
Xem đáp án
Ta có:
2 = 1 × 2
6 = 2 × 3
12 = 3 × 4
20 = 4 × 5
Quy luật dãy số: Mỗi số hạng trong dãy đều bằng tích của 2 số tự nhiên liên tiếp
Vậy số hạng tiếp theo của dãy là:
5 × 6 = 30
Ta có dãy số đầy đủ là: 2; 6; 12; 20; 30;....
Câu 15:
Tám hình chữ nhật y hệt nhau đều có chu vi là 36 cm được ghép thành hình vuông như sau. Tính chu vi của hình vuông đó.
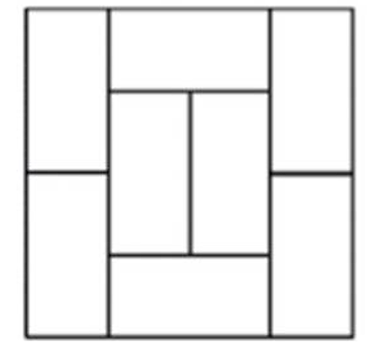
 Xem đáp án
Xem đáp án
Gọi chiều dài và chiều rộng của những hcn con lần lượt là a, b
Theo bài ra:
a + b = 36 : 2 = 18
Theo hình ta sẽ thấy độ dài cạnh hình vuông lớn sẽ bằng: 2 × a = b + a + b
2 × a – a = b + b
a = 2 × b
Vậy chiều dài gấp đôi chiều rộng. Mà tổng chiều dài và chiều rộng là 18 cm nên:
Chiều dài là:
18 : (2 + 1) × 2 = 12 (cm)
Độ dài cạnh hình vuông:
12 × 2 = 24 (cm)
Chu vi hình vuông:
24 × 4 = 96 (cm)
Đáp số: 96 cm.
Câu 16:
 Xem đáp án
Xem đáp án
Điều kiện xác định: x ≠ 3
Để là số hữu tỉ dương thì: (x + 2)(x – 3) > 0
TH1:
TH2:
Vậy x > 3 hoặc x < –2 thỏa mãn yêu cầu đề bài.
Câu 17:
Cho .
a) Tìm x để A là số hữu tỉ dương.
b) Tìm x ∈ ℤ để A ∈ ℤ
 Xem đáp án
Xem đáp án
a)
Để A là số hữu tỉ dương thì x – 1 > 0 hay x > 1
b)
Để A ∈ ℤ thì (x – 1) là ước của 2
Do đó, ta có:
x – 1 ∈ {–1; 1; 2; –2}
x ∈ {0; 2; 3; –1}.
Câu 18:
Tìm số nguyên tố p biết p + 1 cũng là số nguyên tố.
 Xem đáp án
Xem đáp án
Nếu p = 2 ⇒ p + 1 = 2 + 1 = 3 là số nguyên tố (Thỏa mãn)
+ Nếu p > 2 ⇒ p có dạng 2k + 1
Nếu p = 2k + 1 thì
p + 1 = 2k + 1 + 1
= 2k + (1 + 1)
= 2k + 2
= 2(k + 1) chia hết cho 2 và lớn hơn 2 (Loại)
Vậy số nguyên tố p cần tìm là 2.
Câu 19:
Trong một phép chia hai số tự nhiên. có thương là 3 dư 7. Tổng của hai số bị chia và số chia là 243. Tìm số bị chia và số chia ?
 Xem đáp án
Xem đáp án
4 lần số chia là : 243 – 7 = 236
Số bị chia là : 236 : 4 × 3 + 7 = 184
Số chia là : 243 – 184 = 59.
Câu 20:
 Xem đáp án
Xem đáp án
Tổng của 2 số đó là:
123 × 2 = 246
Vì trung bình cộng của hai số tự nhiên là 123, mà số bé là 24, nên số lớn là:
246 – 24 = 222
Vậy số lớn là: 222.
Câu 21:
Trung bình cộng số học sinh của lớp 2 lớp lớp 4A là 39 em số học sinh lớp 4A ít hơn số học sinh lớp 4B là 6 em. Hỏi mỗi lớp có bao nhiêu học sinh ?
 Xem đáp án
Xem đáp án
Tổng số học sinh của hai lớp 4A và 4B là:
39 × 2 = 78 (học sinh)
Lớp 4A có số học sinh là:
(78 − 6) : 2 = 36 (học sinh)
Lớp 4B có số học sinh là:
36 + 6 = 42 (học sinh)
Câu 22:
Người ta trồng ngô trên một mảnh đất hình chữ nhật có chu vi là 500m, chiều rộng kém chiều dài 50m.
a. Tính diện tích mảnh đất đó.
 Xem đáp án
Xem đáp án
a) Tổng chiều dài và rộng mảnh đất:
500 : 2 = 250 (m)
Chiều dài mảnh đất:
(250 + 50) : 2 = 150 (m)
Chiều rộng mảnh đất: 150 – 50 = 100 (m)
Diện tích mảnh đất:
150.100 = 15000 (m2)
Câu 23:
b. Biết rằng cứ trung bình 100m2 thu hoạch được 30kg ngô. Hỏi trên cả thửa ruộng đó, người ta thu hoạch được bao nhiêu tạ ngô ?
 Xem đáp án
Xem đáp án
b) Trung bình cứ 100 m2 thì thu được 30kg ngô.
Thửa ruộng đó thu được: 15000 : 100 × 30 = 4500 (kg) = 45 tạ.
Câu 24:
Tìm hai số có tổng là 234, biết rằng nếu lấy số thứ nhất trừ đi số thứ hai rồi cộng với hiệu của chúng thì được 172.
 Xem đáp án
Xem đáp án
ST1 : Số thứ nhất
ST2 : Số thứu hai
ST1 – ST2 + Hiệu = 172
⇒ ST1 là số lớn ; ST2 là số bé
⇒ Hiệu + Hiệu = 172
⇒ 172 : 2 = 86 = Hiệu
Số thứ nhất là :
(234 + 86) : 2 = 160
Số thứ hai là :
234 – 160 = 74.
Câu 26:
 Xem đáp án
Xem đáp án
Số các số tự nhiên từ 1 đến 1000000 là:
(1000000 – 1) : 1 + 1 = 1000000 (số).
Câu 27:
Số hạng tiếp theo của dãy số sau: 2, 3, 5, 9, 17..., là ?
 Xem đáp án
Xem đáp án
Ta thấy khoảng cách của số 1 với số 2 ra khoảng cách của số 2 với số 3
2 + 1 = 3
1 × 2 = 2
3 + 2 = 5
2 × 2 = 4
5 + 4 = 9
4 × 2 = 8
9 + 8 = 17
8 × 2 = 16
16 + 17 = 33
Vậy số tiếp theo là 33.
Câu 28:
Chứng tỏ rằng các tổng, hiệu sau không chia hết cho 10.
a) A= 98 × 96 × 94 × 92 – 91 × 93 × 95 × 97.
 Xem đáp án
Xem đáp án
Số chia hết cho 10 là số có hàng đơn vị tận cùng là 0.
a)
Hàng đơn vị của phép nhân:
98 × 96 × 94 × 92 là 4 (lấy 8 × 6 × 4 × 2 = 384)
91 × 93 × 95 × 97 là 5 (lấy 1 × 3 × 5 × 7 = 105)
Hiệu số hàng đơn vị là 9 vậy nên A không chia hết cho 10.
Câu 29:
Chứng tỏ rằng các tổng, hiệu sau không chia hết cho 10.
b) B = 405n + 2405 + m2 (m, n ∈ ℕ, n ≠ 0).
 Xem đáp án
Xem đáp án
b)
Ta có:
25 =32
210 =1024
⇒ hàng đơn vị của 2100 là 410 = 6
⇒ hàng đơn vị của 2400 là 64 = 6
⇒ hàng đơn vị của 25 là 2
⇒ hàng đơn vị của 2405 là 2
Hàng đơn vị của 405n là 5
Hàng đơn vị của m2 là 2 hoặc 4 hoặc 6 hoặc 8
Ta thấy không tổng nào 3 hàng đơn vị trên bằng 0.
Vậy B không chia hết cho 10.
Câu 30:
Cho biểu thức A = (x – 4)(x + 3) – (3 – x).
a) Rút gọn biểu thức A.
 Xem đáp án
Xem đáp án
a)
A = (x – 4)(x + 3) – (3 – x)
= x2 + 3x – 4x – 12 – 3 + x
= x2 – 15
Câu 31:
b) Tính giá trị của A khi |x – 1| = 0,5.
 Xem đáp án
Xem đáp án
b)
Khi |x – 1| = 0,5
Với x = 1,5 thì A = 1,52 – 15 = –12,75
Với x = 0,5 thì A = 0,52 – 15 = –14,75
Câu 33:
Ba bạn Hà, Hồng, Đào có tất cả 420 000 đồng. Biết số tiền của Hà bằng số tiền của Hồng và bằng số tiền của Đào. Hỏi Hồng có bao nhiêu tiền ?
 Xem đáp án
Xem đáp án
Quy đồng tử số:
Nếu số tiền của Hà là 12 phần thì số tiền của Hồng là 15 phần, số tiền của Đào là 8 phần
Tổng số phần bằng nhau là:
12 + 15 + 8 = 35 (phần)
Giá trị mỗi phần là:
420000 : 35 = 12000 (đồng)
Hồng có số tiền là:
12000 × 15 = 180000 (đồng)
Đáp số: 180 000 đồng.
Câu 34:
Tìm hai số có tổng là 132. Biết rằng nếu lấy số lớn trừ đi số bé rồi cộng vó tổng của chúng thì được 178.
 Xem đáp án
Xem đáp án
Hiệu 2 số là:
178 – 132 = 46
Số bé là:
(132 – 46) : 2 = 43
Số lớn là:
132 – 43 = 89.
Câu 35:
Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của cắt AD ở K. Chứng minh rằng: AK + CE = BE.
 Xem đáp án
Xem đáp án
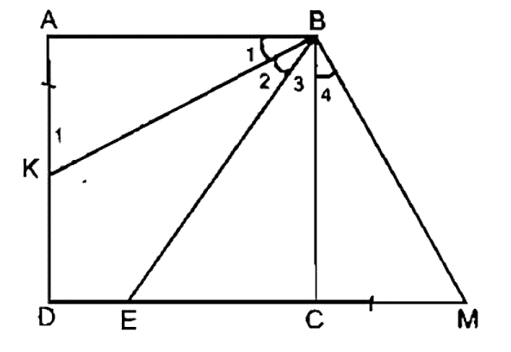
Trên tia đối CD lấy điểm M sao cho CM = AK
Ta có: AK + CE = CM + CE = EM (*)
Xét tam giác ABK và tam giác CBM có:
AB = CB (gt)
AK = CM (theo cách vẽ)
Do đó, tam giác ABK bằng tam giác CBM (c.g.c)
(1)
(2)
Trong tam giác CBM vuông tại C
Từ (1), (2), (3) ta có: (4)
mà (gt)
(chứng minh trên)
(5)
Từ (4) và (5) suy ra:
Do đó, tam giác EBM cân tại E
(**)
Từ (*) và (**) suy ra: AK + CE = BE.
Câu 36:
Chứng minh rằng: A = chia hết cho 3, 7, 15.
 Xem đáp án
Xem đáp án
A =
Do đó, A chia hết cho 3
A =
Do đó, A chia hết cho 7
A =
Do đó, A chia hết cho 15.
Câu 37:
Hùng và Dũng có tất cả 45 viên bi. Nếu Hùng cho đi 5 viên bi thì Hùng có nhiều hơn Dũng 14 viên bi. Hỏi mỗi bạn có bao nhiêu viên bi ?
 Xem đáp án
Xem đáp án
Hùng hơn Dũng số bi là:
14 – 5 = 9 (viên)
Số bi của Hùng là:
( 45 + 9 ) : 2 = 27 (viên)
Số bi của Dũng là:
27 – 9 = 18 (viên)
Đáp số: Hùng: 27 viên bi, Dũng: 18 viên bi.
Câu 38:
Hình chữ nhật dưới đây được cắt thành 7 hình vuông. Biết chu vi của hình chữ nhật là 160 cm, tính diện tích của hình vuông lớn.
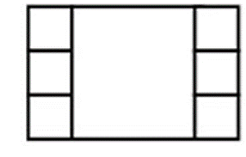
 Xem đáp án
Xem đáp án
Gọi độ dài cạnh của 1 hình vuông nhỏ là a (cm), độ dài cạnh của hình vuông lớn là b (cm)
Chu vi của hình chữ nhật là 160 cm nên ta có:
[(2a + b) + 3a] × 2 = 160
⇒ 5a + b = 80
Mặt khác theo hình vẽ lại có: b = 3a
⇒ 8a = 80 ⇒ a = 10 (cm)
Vậy b = 30 (cm)
Diện tích hình vuông lớn là:
30 × 30 = 900 (cm2)
Đáp số: 900 cm2.
Câu 39:
Một đoàn gồm 98 người muống qua sông. Biết mỗi chuyến đò chỉ chở 9 người kể cả bác lái đò. Hỏi để đưa hết số người trong đoàn người qua sông, bác lái đò cần phải chở bao nhiêu chuyến?
 Xem đáp án
Xem đáp án
Một lần cần đưa số người trong đoàn là: 9 – 1 = 8 (người)
Chở được số chuyến là: 98 : 8 = 3 (chuyến) dư 2 người
Như vậy bác lái đò phải chở thêm 1 chuyến nữa .Bác lái đò phải chở thêm tất cả số chuyến là:
3 + 1 = 4 (chuyến).
Câu 40:
Chứng minh bằng quy nạp:
(1).
 Xem đáp án
Xem đáp án
Với n = 1. Vế trái của (1) = 2, vế phải của (1) = 2
Suy ra (1) đúng với n = 1
Giải sử (1) đúng với n = k. Có nghĩa là ta có:
(2)
Ta phải chứng minh (1) đúng với n = k + 1. Có nghĩa ta phải chứng mình:
Thật vậy:
Vậy (1) đúng khi n = k + 1. Do đó, theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.
Câu 41:
 Xem đáp án
Xem đáp án
Ta có:
(x2 + y2 – 5)2 – 4(x2y2 + 4xy + 4)
= (x2 + y2 – 5)2 – [2(xy + 2)]2
= (x2 + y2 – 5 + 2xy + 4)( x2 + y2 – 5 – 2xy – 4)
= (x – y + 1)(x – y + 3)(x – y – 3).
Câu 42:
Bảy năm về trước tổng số tuổi của ba mẹ con bằng 48. Sáu năm sau tuổi mẹ hơn con nhỏ 30 tuổi và hơn con lớn 24 tuổi. Tính số tuổi mẹ hiện nay.
 Xem đáp án
Xem đáp án
Tổng số tuổi của 3 mẹ con hiện nay là:
48 + 7 + 7 + 7 = 69 (tuổi)
Tuổi con lớn hơn tuổi con bé là:
30 – 24 = 6 (tuổi)
Tuổi con bé là:
(69 – 30 – 6) : 3 =11 (tuổi)
Tuổi mẹ là:
11 + 30 = 41 (tuổi)
Đáp số: 41 tuổi.
Câu 43:
 Xem đáp án
Xem đáp án
A = 48a + 32
A + 16 = 48a + 32 + 16
A + 16 = 48a + 48
A + 16 = 48.(a + 1)
(A +16) chia hết cho 48 và 24.
(A + 16) chia hết cho 24 vậy A chia 24 dư (24 – 16) = 8.
Câu 45:
Công thức tính tích của một dãy số cách đều.
 Xem đáp án
Xem đáp án
Tính bằng cách làm phép nhân như tích bình thường.
Ví dụ: A = 3.5.7.9 = 15.63 = 945.
Câu 46:
Trong một phép chia có thương bằng số bị chia. Thương gấp 3 lần số chia. Tìm số bị chia.
 Xem đáp án
Xem đáp án
Trong một phép chia, thương bằng số bị chia chia cho số chia mà thương bằng số chia sẽ bằng 8 (Tức số bị chia giảm đi 8 lần)
Thương là:
8 × 3 = 24
Số bị chia là:
24 × 8 = 192
Đáp số: 192.
Câu 47:
Một đội y tế có 24 bác sĩ và 108 y tá. Có thể chia đội y tế đó nhiều nhất thành mấy tổ để số bác sĩ cũng như số y tá được chia đều vào mỗi tổ ?
 Xem đáp án
Xem đáp án
Số tổ nhiều nhất chính là ước chung lớn nhất của số bác sĩ và y tá.
Ta có:
24 = 23.3
108 = 22.33
ƯCLN(24, 108) = 22.3 = 12
Vậy có thể chia được nhiều nhất là 12 tổ.
Câu 48:
Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau. Điểm E thuộc OC, nối AE cắt (O) tại M.
a) Chứng minh tứ giác OBME nội tiếp.
 Xem đáp án
Xem đáp án
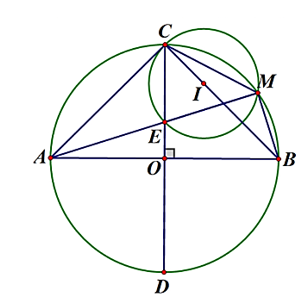
Xét đường tròn (O) có AB là đường kính, M thuộc đường tròn
Do AB vuông góc với CD nên ta có:
Xét tứ giác OBME có:
Do đó, tứ giác OBME là tứ giác nội tiếp.
Câu 49:
b) Chứng minh: AE.AM = AC2 .
 Xem đáp án
Xem đáp án
b, Xét tam giác ACE và tam giác AMC có:
(cùng chắn đường tròn)
Góc chung
Do đó, tam giác ACE đồng dạng với tam giác AMC (g.g)
Câu 50:
c) Xác định vị trí của E để AM = 2MB.
 Xem đáp án
Xem đáp án
Ta có tam giác vuông AOE đồng dạng với tam giác AMB (chung góc )
Do đó, E là trung điểm của OC
Câu 51:
d) Gọi I là tâm đường tròn ngoại tiếp tam giác CME. Chứng minh khi E di chuyển trên OC thì I thuộc một đường thẳng cố định.
 Xem đáp án
Xem đáp án
d)
Ta có:
(góc ở tâm bằng nửa góc nội tiếp cùng chắn cung EC)
Do đó, tam giác EIC vuông cân tại I
không đổi
Do đó, I luôn thuộc BC cố định.
Câu 52:
Một đội công nhân có 8 người làm trong 6 ngày đắp được 360m đường. Hỏi một đội công nhân có 12 người đắp xong 1080m đường trong bao nhiêu ngày ?
 Xem đáp án
Xem đáp án
8 người trong một ngày đắp được số m đường là:
360 : 6 = 60 (m).
12 người trong một ngày đắp được số m đường là:
12 × 60 : 8 = 90 (m).
Số ngày 12 người đắp trong 1080 m đường là:
1080 : 90 = 12 (ngày)
Đáp số: 12 ngày.
Câu 53:
Cô giáo có một số kẹo. Nếu cô chia cho mỗi bạn 3 cái kẹo thì dư 5 cái kẹo, còn nếu cô chia cho mỗi bạn 4 cái kẹo thì thiếu 12 cái kẹo. Hỏi cô có bao nhiêu cái kẹo ?
 Xem đáp án
Xem đáp án
Số kẹo đủ để chia cho mỗi em 4 cái nhiều hơn số kẹo đủ để chia cho mỗi em 3 cái là:
12 + 5 = 17 (cái)
Mỗi em chia 4 cái nhiều hơn mỗi em chia 3 cái là:
4 – 3 = 1 (cái)
Số em được cô giáo chia kẹo:
17 : 1 = 17 (em)
Cô giáo có số kẹo là:
17 × 3 + 5 = 56 (cái)
Đáp số: 56 cái kẹo.
Câu 54:
Cho tam giác ABC có cạnh BC cố định, đường trung tuyến BM = 1cm. Hỏi đỉnh A di động trên đường nào ?
 Xem đáp án
Xem đáp án
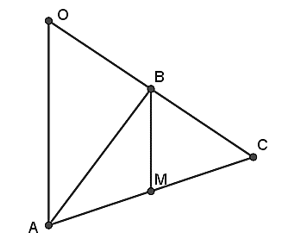
Gọi O là điểm đối xứng với C qua B.
BC cố định nên O cố định.
Có: B là trung điểm OC; M là trung điểm AC
⇒ BM là đường trung bình của OAC
⇒ OA = 2 cm
Mà O cố định nên A di chuyển trên đường tròn tâm O bán kính 2 cm.
Câu 55:
Trong một phép chia có số bị chia là 155 số dư là 12. Tìm số chia và thương.
 Xem đáp án
Xem đáp án
Gọi thương và số chia là a và b.
Ta có:
a × b +12 = 155
⇒ a × b =143
Mà 143 = 13 × 11
Vậy a = 13, b = 11.
Câu 56:
 Xem đáp án
Xem đáp án
Tổng của hai số là một số lẻ do đó là tổng của một số chẵn và một số lẻ.
Mà hai số đó là số nguyên tố nên số chẵn là 2 suy ra số còn lại là
139 – 2 = 137.
Câu 57:
 Xem đáp án
Xem đáp án
Xét phép chia:
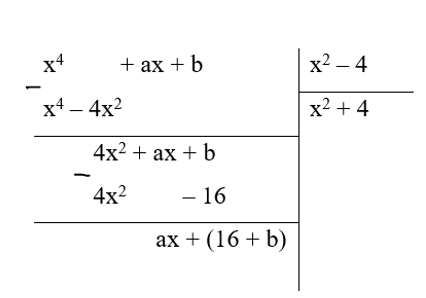
Để chia hết cho x2 – 4 thì đa thức dư ax + b + 16 phải đồng nhất 0
Do đó, a = 0, b = –16
Vậy với a = 0, b = –16 thì chia hết cho x2 – 4.
Câu 58:
Cho 2 số tự nhiên a và b khác 0, biết a là số chẵn lớn nhất bé hơn 20 và tổng của 2 số gấp 5 lần hiệu của a – b. Tìm b.
 Xem đáp án
Xem đáp án
Ta có: a = 18
Theo đề bài, có:
18 + b = 5 × (18 – b)
⇒ 18 + b = 90 – 5 × b
⇒ 6 × b = 72
⇒ b = 12.
Câu 59:
Có một bao gạo từ bao gạo đó người ta lấy ra bao gạo là kg. Hỏi nếu lấy bao gạo là mấy kg ?
 Xem đáp án
Xem đáp án
bao gạo là kg nên ta có cân nặng của bao gạo là:
(kg)
Vậy bao gạo là: (kg).
Câu 60:
Một hình bình hành có tổng độ dài hai cạnh kề nhau bằng 22cm. Khi đó, chu vi của hình bình hành đó là ?
 Xem đáp án
Xem đáp án
Tổng độ dài hai cạnh kề là 22 cm. Nên tổng độ dài hai cạnh còn lại cũng là 22 cm.
Chu vi hình bình hành là: 22 + 22 = 44 (cm).
Câu 61:
2,7giờ = ... giờ...phút.
 Xem đáp án
Xem đáp án
2,7 giờ = 2 giờ + 0,7
0,7 giờ = 0,7 × 60 phút = 42 phút
Do đó 2,7 giờ = 2 giờ 42 phút.
Câu 62:
Tìm số thập phân a,b biết a,b × 9,9 = aa,bb.
 Xem đáp án
Xem đáp án
Ta có :
a,b × 9,9 = aa,bb
a,b × 10 × 9,9 × 10 = aa,bb × 100
ab × 99 = aabb
ab × 99 = 11 × (a × 100 + b )
ab × 9 = a × 100 + b
a × 90 + b × 9 = a × 100 + b
b × 8 = a × 10
b × 4 = a × 5
Vậy a = 4; b = 5.
Câu 63:
Tìm x, biết: (15 + x ) : 3 = 315 : 312.
 Xem đáp án
Xem đáp án
(15 + x ) : 3 = 315 : 312
(15 + x ) : 3 = 33
15 + x = 81
x = 66.
Câu 64:
Tìm chữ số a để 23a là số nguyên tố.
 Xem đáp án
Xem đáp án
Để 23a là 1 số nguyên tố thì a là số lẻ.
Ta thay các số lẻ vào a thì ta được:
+ 231 không phải là số nguyên tố vì chia hết cho 3 và 11.
+ 233 là số nguyên tố.
+ 235 không phải là số nguyên tố vì chia hết cho 5.
+ 237 không phải là số nguyên tố vì chia hết cho 3.
+ 239 là số nguyên tố.
Vậy a = {3; 9}.
Câu 65:
Tìm 3 số tự nhiên sao cho tổng nghịch đảo của chúng bằng 2.
 Xem đáp án
Xem đáp án
Theo đề bài ta có:
Không mất tính tổng quát, giả sử:
Vậy a = 1, b = c = 2.
Câu 66:
Tìm số nguyên tố o sao cho p + 2 ; p + 6 ; p + 8 ; p + 12 ; p + 14 cũng là các số nguyên tố.
 Xem đáp án
Xem đáp án
Xét p = 2 thì p + 2 = 2 + 2 = 4 là hợp số [loại]
Xét p = 3 thì p + 6 = 3 + 6 = 9 là hợp số [loại]
Xét p = 5 thì p + 2 ; p + 6 ; p + 8 ; p + 12 ; p + 14 đều là SNT [thỏa mãn]
Xét p > 5 Thì có các dạng : 5k + 1; 5k + 2; 5k + 3; 5k + 4
Nếu p = 5k + 1 thì p + 14 = 5k + 1 + 14 = 5k + 15 là hợp số mà p > 5 nên p = 5k + 1 là hợp số [loại]
Nếu p = 5k + 2 thì p + 8 = 5k + 2 + 8 = 5k + 10 là hợp số [loại]
Nếu p = 5k + 3 thì p + 12 = 5k + 3 + 12 = 5k + 15 là hợp số [loại]
Nếu p = 5k + 4 thì p + 6 = 5k + 6 = 4 + 6 = 5k + 10 là hợp số [loại]
Do đó, trường hợp p > 5 không có số nào thỏa mãn
Vậy p = 5 thỏa mãn đề bài.
Câu 67:
Tìm x: 35 – 5(x – 1) = 10.
 Xem đáp án
Xem đáp án
35 – 5(x – 1) = 10
5(x – 1) = 35 – 10
5(x – 1) = 25
x – 1 = 25 : 5
x – 1 = 5
x = 5 + 1
x = 6.
Câu 68:
Một thùng sữa có 10 vỉ, mỗi vỉ có 4 hộp, mỗi hộp có giá 4000 đồng. Hỏi nếu mua 5 thùng thì hết bao nhiêu tiền ?
 Xem đáp án
Xem đáp án
Mỗi thùng sữa có số hộp sữa là:
4 × 10 = 40 (hộp)
Vậy 5 thùng sữa thì có số hộp sữa là:
40 × 5 = 200 (hộp)
Vậy mua 5 thùng hết số tiền là:
4000 × 200 = 800000 (đồng)
Đáp số: 800000 đồng.
Câu 70:
Số nguyên tố nhỏ hơn 1000000 là số bao nhiêu ?
 Xem đáp án
Xem đáp án
Các số nguyên tố nhỏ hơn 1000000 là:
2 3 5 7 11 13 17 19 23 29
31 37 41 43 47 53 59 61 67 71
73 79 83 89 97 101 103 107 109 113
127 131 137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223 227 229
233 239 241 251 257 263 269 271 277 281
283 293 307 311 313 317 331 337 347 349
353 359 367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457 461 463
467 479 487 491 499 503 509 521 523 541
547 557 563 569 571 577 587 593 599 601
607 613 617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719 727 733
739 743 751 757 761 769 773 787 797 809
811 821 823 827 829 839 853 857 859 863
877 881 883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997 1009 1013
1019 1021 1031 1033 1039 1049 1051 1061 1063 1069
1087 1091 1093 1097 1103 1109 1117 1123 1129 1151
1153 1163 1171 1181 1187 1193 1201 1213 1217 1223
1229 1231 1237 1249 1259 1277 1279 1283 1289 1291
1297 1301 1303 1307 1319 1321 1327 1361 1367 1373
1381 1399 1409 1423 1427 1429 1433 1439 1447 1451
1453 1459 1471 1481 1483 1487 1489 1493 1499 1511
1523 1531 1543 1549 1553 1559 1567 1571 1579 1583
1597 1601 1607 1609 1613 1619 1621 1627 1637 1657
1663 1667 1669 1693 1697 1699 1709 1721 1723 1733
1741 1747 1753 1759 1777 1783 1787 1789 1801 1811
1823 1831 1847 1861 1867 1871 1873 1877 1879 1889
1901 1907 1913 1931 1933 1949 1951 1973 1979 1987
1993 1997 1999 2003 2011 2017 2027 2029 2039 2053
2063 2069 2081 2083 2087 2089 2099 2111 2113 2129
2131 2137 2141 2143 2153 2161 2179 2203 2207 2213
2221 2237 2239 2243 2251 2267 2269 2273 2281 2287
2293 2297 2309 2311 2333 2339 2341 2347 2351 2357
2371 2377 2381 2383 2389 2393 2399 2411 2417 2423
2437 2441 2447 2459 2467 2473 2477 2503 2521 2531
2539 2543 2549 2551 2557 2579 2591 2593 2609 2617
2621 2633 2647 2657 2659 2663 2671 2677 2683 2687
2689 2693 2699 2707 2711 2713 2719 2729 2731 2741
2749 2753 2767 2777 2789 2791 2797 2801 2803 2819
2833 2837 2843 2851 2857 2861 2879 2887 2897 2903
2909 2917 2927 2939 2953 2957 2963 2969 2971 2999
3001 3011 3019 3023 3037 3041 3049 3061 3067 3079
3083 3089 3109 3119 3121 3137 3163 3167 3169 3181
3187 3191 3203 3209 3217 3221 3229 3251 3253 3257
3259 3271 3299 3301 3307 3313 3319 3323 3329 3331
3343 3347 3359 3361 3371 3373 3389 3391 3407 3413
3433 3449 3457 3461 3463 3467 3469 3491 3499 3511
3517 3527 3529 3533 3539 3541 3547 3557 3559 3571
3581 3583 3593 3607 3613 3617 3623 3631 3637 3643
3659 3671 3673 3677 3691 3697 3701 3709 3719 3727
3733 3739 3761 3767 3769 3779 3793 3797 3803 3821
3823 3833 3847 3851 3853 3863 3877 3881 3889 3907
3911 3917 3919 3923 3929 3931 3943 3947 3967 3989
4001 4003 4007 4013 4019 4021 4027 4049 4051 4057
4073 4079 4091 4093 4099 4111 4127 4129 4133 4139
4153 4157 4159 4177 4201 4211 4217 4219 4229 4231
4241 4243 4253 4259 4261 4271 4273 4283 4289 4297
4327 4337 4339 4349 4357 4363 4373 4391 4397 4409
4421 4423 4441 4447 4451 4457 4463 4481 4483 4493
4507 4513 4517 4519 4523 4547 4549 4561 4567 4583
4591 4597 4603 4621 4637 4639 4643 4649 4651 4657
4663 4673 4679 4691 4703 4721 4723 4729 4733 4751
4759 4783 4787 4789 4793 4799 4801 4813 4817 4831
4861 4871 4877 4889 4903 4909 4919 4931 4933 4937
4943 4951 4957 4967 4969 4973 4987 4993 4999 5003
5009 5011 5021 5023 5039 5051 5059 5077 5081 5087
5099 5101 5107 5113 5119 5147 5153 5167 5171 5179
5189 5197 5209 5227 5231 5233 5237 5261 5273 5279
5281 5297 5303 5309 5323 5333 5347 5351 5381 5387
5393 5399 5407 5413 5417 5419 5431 5437 5441 5443
5449 5471 5477 5479 5483 5501 5503 5507 5519 5521
5527 5531 5557 5563 5569 5573 5581 5591 5623 5639
5641 5647 5651 5653 5657 5659 5669 5683 5689 5693
5701 5711 5717 5737 5741 5743 5749 5779 5783 5791
5801 5807 5813 5821 5827 5839 5843 5849 5851 5857
5861 5867 5869 5879 5881 5897 5903 5923 5927 5939
5953 5981 5987 6007 6011 6029 6037 6043 6047 6053
6067 6073 6079 6089 6091 6101 6113 6121 6131 6133
6143 6151 6163 6173 6197 6199 6203 6211 6217 6221
6229 6247 6257 6263 6269 6271 6277 6287 6299 6301
6311 6317 6323 6329 6337 6343 6353 6359 6361 6367
6373 6379 6389 6397 6421 6427 6449 6451 6469 6473
6481 6491 6521 6529 6547 6551 6553 6563 6569 6571
6577 6581 6599 6607 6619 6637 6653 6659 6661 6673
6679 6689 6691 6701 6703 6709 6719 6733 6737 6761
6763 6779 6781 6791 6793 6803 6823 6827 6829 6833
6841 6857 6863 6869 6871 6883 6899 6907 6911 6917
6947 6949 6959 6961 6967 6971 6977 6983 6991 6997
7001 7013 7019 7027 7039 7043 7057 7069 7079 7103
7109 7121 7127 7129 7151 7159 7177 7187 7193 7207
7211 7213 7219 7229 7237 7243 7247 7253 7283 7297
7307 7309 7321 7331 7333 7349 7351 7369 7393 7411
7417 7433 7451 7457 7459 7477 7481 7487 7489 7499
7507 7517 7523 7529 7537 7541 7547 7549 7559 7561
7573 7577 7583 7589 7591 7603 7607 7621 7639 7643
7649 7669 7673 7681 7687 7691 7699 7703 7717 7723
7727 7741 7753 7757 7759
Câu 71: Tìm x: (–12) – (13 – x) = –15 – (–17). (–12) – (13 – x) = –15 – (–17) (–12) – (13 – x) = –15 + 17 (–12) – (13 – x) = 2 –13 – x = 2 + 12 –13 – x = 14 x =14 – 13 x = 1.
Câu 74:
Biểu diễn các hiệu sau thành tổng rồi tính:
a) (–23) – 12
b) 43 – (–53)
c) (–15) – (–17)
d) 14 – 20
 Xem đáp án
Xem đáp án
a)
(–23) – 12 = (–23) + (–12) = –35
b)
43 – (–53) = 43 + 53 = 96
c)
(–15) – (–17) = (–15) + 17 = 2
d)
14 – 20 = 14 + (–20) = –6.
Câu 75:
Tính tổng của tất cả các số có 5 chữ số khác nhau được lập bởi 6 chữ số 1; 2; 3; 4; 5; 6.
 Xem đáp án
Xem đáp án
Số các số là : 6 × 5 × 4 × 3 × 2 = 720 ( số )
Khi lập 1 chữ số ở hàng chục nghìn thì các chữ số ở hàng còn lại lặp đi lặp lại 120 lần.
Hàng chục nghìn : (1 + 2 + 3 + 4 + 5 + 6) × 120 × 10000 = 25200000
Hàng nghìn : (1 + 2 + 3 + 4 + 5 + 6) × 120 × 1000 = 2520000
Hàng trăm : (1 + 2 + 3 + 4 + 5 + 6) × 120 × 100 = 252000
Hàng chục : (1 + 2 + 3 + 4 + 5 + 6) × 120 × 10 = 25200
Hàng đơn vị : (1 + 2 + 3 + 4 + 5 + 6) × 120 × 1 = 2520
Vậy tổng các số là : 25200000 + 2520000 + 252000 + 25200 + 2520 = 27999720.
Câu 76:
Cho đường tròn (O; R) và điểm A nằm bên ngoài đường tròn. Kẻ tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
1. Chứng minh ABOC là tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
1)
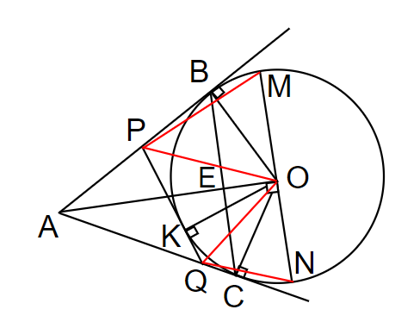
Vì AB là tiếp tuyến (O; R) nên AB vuông góc với OB
Vì AC là tiếp tuyến (O; R) nên AC vuông góc với OC
Ta có:
Do đó, tứ giác ABOC nội tiếp đường trònCâu 77:
2. Gọi E là giao điểm của BC và OA. Chứng minh BE vuông góc với OA và OE.OA = R2.
 Xem đáp án
Xem đáp án
Vì tiếp tuyến AB cắt tiếp tuyến AC tại A nên AB = AC và BO = CO
Do đó, AO là đường trung trực ứng với BC
Do đó, AO vuông góc với BC hay BE vuông góc với AO
Áp dụng hệ thức lượng trong tam giác vuông OBA có:
OA.OE = OB2 hay OA.OE = R2 vì OB = R
Câu 78:
3. Trên cung nhỏ BC của đường tròn (O; R) lấy điểm K bất kỳ (K khác B và C). Tiếp tuyến tại K của đường tròn (O; R) cắt AB, AC theo thứ tự tại P, Q. Chứng minh tam giác APQ có chu vi không đổi khi K chuyển động trên cung nhỏ BC.
 Xem đáp án
Xem đáp án
Vì tiếp tuyến BP cắt tiếp tuyến PK tại P
⇒ PB = PK
Vì tiếp tuyến KQ cắt tiếp tuyến QC tại Q nên KQ = QC
Ta có:
Chu vi tam giác APQ = AP + PQ + AQ = AP + PK + KQ + AQ
= (AP + PB) + (QC + AQ) = AB + AC
Vì AB + AC không thay đổi khi K chuyển động trên cung nhỏ BC nên chu vi tam giác AQP không thay đổi khi K thay đổi trên cung nhỏ BC
Câu 79:
Chứng minh rằng: Nếu p là số nguyên tố lớn hơn 3 thì (p – 1).(p + 1) chia hết cho 24.
 Xem đáp án
Xem đáp án
p là số nguyên tố lớn hơn 3 ⇒ p không chia hết cho 2 cho 3
Ta có : p không chia hết cho 2
⇒ p – 1 và p + 1 là 2 số chẵn liên tiếp ⇒ (p – 1)(p + 1) chia hết cho 8 (1)
Mặt khác: p không chia hết cho 3
Nếu p = 3k +1 thì p – 1 = 3k chia hết cho 3 ⇒ (p – 1)(p + 1) chia hết cho 3
Tương tự:
Nếu p = 3k + 2 thì p + 1 = 3k + 3 chia hết cho 3 ⇒ (p – 1)(p + 1) chia hết cho 3 (2)
Từ (1)(2) ⇒ (p – 1)(p + 1) chia hết cho 8 cho 3 mà (8; 3) = 1 ⇒ (p – 1)(p + 1) chia hết cho 24.
Câu 80:
 Xem đáp án
Xem đáp án
45 = 32.5
⇒ Ư(45) ={1; 3; 5; 9; 15; 45}
Các ước tự nhiên có hai chữ số của 45 là 15; 45
Số các ước tự nhiên có hai chữ số của 45 là 2.
Câu 81:
Hai thùng đựng 275 l đầu. Nếu rót từ thùng thứ nhất sang thùng thứ hai 33l dầu thì thùng thứ hai hơn thùng thứ nhất 15l đầu. Hỏi mỗi thùng lúc đầu có bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
Lúc đầu, thùng thứ nhất có số lít dầu là:
(275 – 15) : 2 + 33 = 163 (lít)
Lúc đầu, thùng thứ hai có số lít dầu là:
275 – 163 = 112 (lít)
Câu 82:
Một cửa hàng có 5 kiện hàng. Mỗi kiện hàng có 10 gói hàng, mỗi gói hàng có 8 sản phẩm . Hỏi trong 5 kiện hàng đó có tất cả bao nhiêu sản phẩm? (giải bằng 2 cách)
 Xem đáp án
Xem đáp án
Cách 1:
5 kiện có số sản phẩm là:
5 × 10 × 8 = 400 (sản phẩm)
Cách 2:
5 kiện có số gói hàng là:
5 × 10 = 50 (gói)
50 gói có số sản phẩm là:
50 × 8 = 400 (sản phẩm)
Đáp số: 400 sản phẩm.
Câu 83:
Cho tam giác ABC vuông tại A, . Tia phân giác của cắt cạnh AC tại M. Lấy K trên cạnh BC sao cho BK = BA.
a) Chứng minh tam giác ABM và tam giác KBM.
 Xem đáp án
Xem đáp án
a)
Xét tam giác ABM và tam giác KBM có:
BA = BK
(vì BM là phân giác)
Chung BM
Do đó, tam giác ABM bằng tam giác KBM (c.g.c)
Câu 84:
b) Gọi E là giao điểm của các đường thẳng AB và KM. Chứng minh tam giác MEC cân.
 Xem đáp án
Xem đáp án
b)
Từ (a) ta có: MA = MK ,
Do đó, MK vuông góc với BC
Xét tam giác MAE và tam giác MKC có:
vì MK vuông góc với BC
MA = MK
Do đó, tam giác MAE bằng tam giác MKC (g.c.g)
⇒ ME = MC
Do đó, tam giác MEC cân tại M
Câu 85:
c) Chứng minh: Tam giác BEC đều.
 Xem đáp án
Xem đáp án
Từ (b) ta có: AE = CK
⇒ BE = BA + AE = BK + CK = BC
Do đó, tam giác BCE cân tại B
Mà
Do đó, tam giác BCE đều
Câu 86:
d) Kẻ AH vuông góc với EM tại H. Các đường thẳng AH và EC cắt nhau tại N. Chứng minh KN vuông góc AC.
 Xem đáp án
Xem đáp án
d)
Ta có tam giác BCE đều , EK vuông góc với BC nên EK là phân giác
Xét tam giác EAH và tam giác ENH có:
vì EK là phân giác
Chung EH
vì AH vuông góc với EM
Do đó, tam giác AHE bằng tam giác NHE (g.c.g)
⇒ EA = EN
Mà
Do đó, tam giác EAN đều
Mà EH vuông góc với AN nên EN là trung trực của AN
Do M thuộc EH nên MN = MA
Mà MA = MK nên MN = MK
Ta có tam giác BCE đều, BN vuông góc EC, CA vuông góc BE, EK vuông góc BC
Do đó, BN, CA, EK là trung trực của EC, BE, BC
Do đó, A, K, N là trung điểm của BE, BC, CE
Mà BC = CE = EB
Nên EA = AB = BK = KC = CN = NE
Nên CN = CK
Ta có: MN = MK, CN = CK
Do đó, M, C thuộc trung trực của KN
MC là trung trực của KN
MC vuông góc với KN
AC vuông góc với KN.
Câu 87:
An và Bình nhận làm chung một công việc. Nếu An làm một mình thì sau 3 giờ sẽ xong việc, còn nếu Bình làm một mình thì sau 6 giờ sẽ xong. Hỏi cả hai người cùng làm thì sau mấy giờ sẽ xong công việc đó ?
 Xem đáp án
Xem đáp án
1 giờ An làm được là: (công việc)
1 giờ Bình làm được là: (công việc)
1 giờ hai người làm được là: (công việc)
Vậy hai người cần làm sau số giờ thì hoàn thành công việc là:
(giờ).
Câu 88:
Một người bán gà lần thứ nhất bán số gà lần thứ 2 bán số gà còn lại, như thế, lần thứ nhất bán nhiều hơn lần thứ hai 4 con. Hỏi người đó bán tất cả bao nhiêu con gà ?
 Xem đáp án
Xem đáp án
Coi toàn bộ số gà là 9 phần.
Số gà đã bán lần 1 là 4 phần
Số gà còn lại sau khi bán lần thứ nhất ứng với số phần là:
9 – 4 = 5 (phần)
Số gà bán lần thứ hai ứng với: (phần)
4 con gà tương ứng với:
4 – 3 = 1 (phần)
Số gà đem đi bán là:
4 × 9 = 36 (con)
Đáp số: 36 con.
Câu 89:
Một tổ sản xuất trong 11 ngày đầu mỗi ngày làm được 112 sản phẩm, trong 14 ngày sau mỗi ngày làm được 125 sản phẩm. Hỏi tổ sản xuất đó đã làm được tất cả bao nhiêu sản phẩm ?
 Xem đáp án
Xem đáp án
Số sản phẩm tổ đó sản xuất được trong 11 ngày đầu là:
11 × 112 = 1232 (sản phẩm)
Số sản phẩm tổ đó sản xuất được trong 14 ngày sau là:
14 × 125 = 1750 (sản phẩm)
Tổ sản xuất đó đã làm được số sản phẩm là:
1232 + 1750 = 2982 (sản phẩm)
Đáp số: 2982 sản phẩm.
Câu 90:
Một đồng hồ treo tường có đặc điểm như sau: Khi kim phút chỉ đúng số 12 thì đồng hồ đánh số chuông tương ứng với số mà kim giờ chỉ. Hỏi một ngày đồng hồ phải đánh bao nhiêu tiếng chuông ?
 Xem đáp án
Xem đáp án
Một ngày đồng hồ đó đánh là:
(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12) . 2 = 156 (tiếng chuông)
Đáp số: 156 tiếng chuông.
Câu 91:
Tìm số tự nhiên x, y sao cho (2x + 1)(y – 5) = 12.
 Xem đáp án
Xem đáp án
(2x + 1)(y – 5) = 12
⇒ 2x + 1 ∈ Ư(12)
Vì x ≥ 0 ⇒ 2x + 1 ≥ 1
Mà 2x + 1 chia 2 dư 1
⇒ 2x + 1 ∈ {1; 3}.
Ta có bảng sau:
|
2x + 1 |
1 |
3 |
|
2x |
0 |
2 |
|
x |
0 |
1 |
|
y – 5 |
12 |
4 |
|
y |
17 |
9 |
Vậy : (x; y) ∈ {(0; 17); (1; 9)}.
Câu 92:
Tìm số nguyên tố p sao cho p + 4 và p + 8 cùng là số nguyên tố.
 Xem đáp án
Xem đáp án
Xét p = 2 ⇒ p + 4 = 6 (không là số nguyên tố) ⇒ loại
Xét p = 3 ⇒ p + 4 = 7 (TM) và p + 8 = 11 (TM)
Nếu p > 3 , p nguyên tố ⇒ p có dạng 3k + 1 hoặc 3k + 2 (k nguyên dương)
Với p = 3k + 1 ⇒ p + 8 = 3k + 1 + 8 = 3k + 9 chia hết cho 3 ⇒ loại
Với p = 3k + 2 ⇒ p + 4 = 3k + 2 + 4 = 3k + 6 chia hết cho 3 ⇒ loại
Do đó, với mọi p > 3 đều không thỏa mãn
Vậy p = 3 là giá trị thỏa mãn cần tìm.
Câu 93:
Tìm số đối của các số sau:
a) –15
b) –(–3)
c) 5 – a (a thuộc ℤ)
d) x – 10 (x thuộc ℤ)
 Xem đáp án
Xem đáp án
a)
Số đối của –15 là 15
b)
Số đối của –(–3) = –3
c)
Số đối của 5 – a là a – 5
d)
Số đối của x – 10 là 10 – x.
Câu 94:
Với bốn chữ số 2 và các dấu phép tính +, –, × , :, hãy viết các biểu thức có giá trị bằng 13.
 Xem đáp án
Xem đáp án
22 : 2 + 2 = 13.
Câu 95:
Định lý lớn Fermat.
 Xem đáp án
Xem đáp án
Với n, x, y, z ∈ ℕ và n > 2 thì phương trình: xn + yn = zn vô nghiệm.
Câu 96:
Để lát nền một phòng họp người ta phải dùng hết 500 viên gạch lát nền hình vuông có cạnh 4 dm. Hỏi diện tích phòng họp đó là bao nhiêu mét vuông? (Biết diện tích phần mạch vữa không đáng kể).
 Xem đáp án
Xem đáp án
Diện tích 1 viên gạch là: 4 × 4= 16 (dm2)
Diện tích phòng họp đó là: 600 × 16 = 8000 (dm2) = 80 m2.
Đáp số: 80 m2.
Câu 97:
 Xem đáp án
Xem đáp án
Tổng số tuổi của bố, mẹ, Mai và em là:
21 × 4 = 84 (tuổi)
Tổng số tuổi của bố, mẹ và em là:
25 × 3 = 75 (tuổi)
Tuổi của Mai là:
84 – 75 = 9 (tuổi)
Tuổi của em Mai là:
9 – 4 = 5 (tuổi)
Câu 98:
Hai số có tổng là 346. Biết số bé là số có hai chữ số và khi viết thêm chữ số 2 vào trước số bé thì được số lớn.Tìm số lớn.
 Xem đáp án
Xem đáp án
Gọi 2 số cần tìm là và
Ta có: 2ab + ab = 346
⇒ 2ab – ab = 346 – 2 × ab
⇒ 200 = 346 – 2 × ab
⇒ ab × 2 = 346 – 200
⇒ ab × 2= 146
⇒ ab = 146 : 2
⇒ ab = 73
Vậy 2 số cần tìm là 73 và 273.
Câu 99:
Cho tam giác nhọn ABC. Các đường cao AD và BE cắt nhau tại H. Đường thẳng vuông góc với AB tại A cắt BE ở K. Chứng minh tam giác EAK đồng dạng tam giác ECH.
 Xem đáp án
Xem đáp án
Vì H là giao của 2 đường cao AD, BE trong tam giác nên H là trực tâm.
Do đó, CH cũng là đường cao của tam giác ABC hay CH vuông góc với AB
Mà AK vuông góc với AB (giả thiết)
Suy ra: CH song song với AK
(so le trong)
Xét tam giác EAK và ECH có:
Do đó, tam giác EAK đồng dạng với tam giác ECH (g.g).
Câu 100:
Tìm hai số nguyên tố có tổng bằng 309.
 Xem đáp án
Xem đáp án
Vì tổng 2 số nguyên tố là 1 số lẻ nên 1 trong 2 số phải là chẵn.
⇒ 1 số là 2 (Vì 2 là số chẵn nguyên tố duy nhất)
⇒ Số còn lại = 309 – 2 = 307.
Câu 102:
Viết thêm 3 số hạng của mỗi dãy số sau:
a) 1, 2, 3, 5, 8, 13, ...
b) 1, 4, 9, 16, 25, 36, ...
 Xem đáp án
Xem đáp án
a) 1, 2, 3, 5, 8, 13, 21, 34, 55. (số sau bằng tổng hai số trước liền kề)
b) 1, 4, 9, 16, 25, 36, 49, 64, 81. (dãy số chính phương: bình phương của các số tự nhiên liên tiếp)
Câu 104:
Chứng minh: 52n+1.2n+2 + 3n+2.22n+1 chia hết cho 38.
 Xem đáp án
Xem đáp án
52n+1.2n+2 + 3n+2.22n+1 = 52n.5.2n.22+3n.32.22n.2
= 252n.2n.5.4 + 3n.4n.9.2
= 50n.20 + 12n.18
50 đồng dư với 12 (mod 38)
Do đó, 50n đồng dư với 12n (mod 38)
Do đó, 50n.20 + 12n.18 đồng dư với 12n.20 + 12n.18 = 12n.38 đồng dư với 0 (mod 38)
Vậy 52n+1.2n+2 + 3n+2.22n+1 chia hết cho 38.
Câu 105:
Có bao nhiêu số nguyên là tổng của ba phần tử phân biệt của tập hợp {1; 4; 7; 10; 13; 16; 19}.
 Xem đáp án
Xem đáp án
Có 13 số nguyên: {12; 15; 18; 21; 24; 27; 30; 33; 36; 39; 42; 45; 48}.