Cho tam giác ABC (AB = AC), trung tuyến BD. Lấy điểm E sao cho C là trung điểm AE. Chứng minh rằng BE = 2BD.
Giải bởi Vietjack
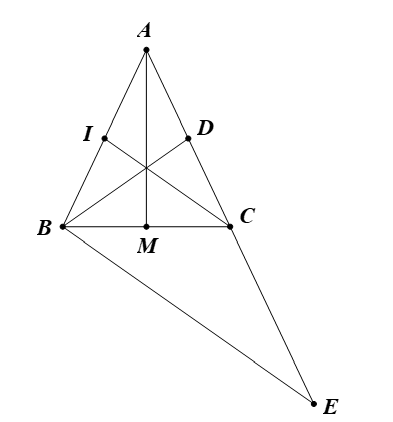
Gọi I, M lần lượt là trung điểm của AB, BC.
Xét ∆ABM và ∆ACM, có:
AM là cạnh chung;
AB = AC (giả thiết);
BM = CM (M là trung điểm BC).
Do đó ∆ABM = ∆ACM (c.c.c).
Ta có D, I lần lượt là trung điểm của AC, AB.
Suy ra AC = 2CD và AB = 2BI.
Mà AB = AC (giả thiết).
Do đó 2CD = 2BI hay CD = BI.
Xét ∆BCI và ∆CBD, có:
BC là cạnh chung;
(∆ABM = ∆ACM);
BI = CD (chứng minh trên).
Do đó ∆BCI = ∆CBD (c.g.c).
Suy ra CI = BD (cặp cạnh tương ứng).
Tam giác ABE có C, I lần lượt là trung điểm của AE, AB.
Suy ra CI là đường trung bình của tam giác ABE.
Do đó CI // BE và 2CI = BE.
Mà CI = BD.
Vậy BE = 2BD.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn tâm O, từ điểm M ở bên ngoài đường tròn (O), kẻ các tiếp tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D; O và B nằm về hai phía so với cát tuyến MCD).
a) Chứng minh tứ giác MAOB nội tiếp.
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng M, N, P, Q cùng nằm trên một đường tròn.
c) Gọi H là giao điểm của AB và OM. Chứng minh AB là phân giác của .
c) Gọi K là giao điểm của SC với mặt phẳng (AMN). Chứng minh AMKN có hai đường chéo vuông góc với nhau.
Cho tam giác ABC vuông cân tại A. Lấy điểm D trên cạnh AB, lấy điểm E trên cạnh AC sao cho AD = AE. Qua D, A kẻ các đường thẳng vuông góc với BE cắt BC theo thứ tự tự I và K. M là giao điểm của ID và CA. Chứng minh rằng:
a) AM = AC.
Tìm số bộ (x, y, z, t) nguyên không âm thỏa mãn x + y + z + t = 40 và x, y, z, t là các số lẻ.
Cho tam giác ABC, trung tuyến AM. Gọi D là 1 điểm trên cạnh AC sao cho , BD cắt AM tại I. Chứng minh AI = IM.
Chứng minh rằng có vô số bộ ba số tự nhiên (a, b, c) sao cho a, b, c nguyên tố cùng nhau và số n = a2b2 + b2c2 + c2a2 là số chính phương.
Cho phương trình x2 – 5x + 3 = 0 có hai nghiệm x1, x2. Hãy lập phương trình bậc hai có hai nghiệm là y1 = 2x1 – x2; y2 = 2x2 – x1.
Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo. Gọi M, N theo thứ tự là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. Gọi F là giao điểm của CN và AB.
a) Chứng minh tứ giác AMCN là hình bình hành.
Có bao nhiêu giá trị nguyên của m để hàm số y = mx4 + (m2 – 4)x2 + 2 có đúng một điểm cực đại và không có điểm cực tiểu?
Xác định hệ số a và b để đa thức f(x) = x4 + ax2 + b chia hết cho g(x) = x2 – 3x + 2. Tìm đa thức thương.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = 2a và vuông góc với đáy. Gọi M, N lần lượt là hình chiếu của A trên SB, SD.
a) Chứng minh AM ⊥ (SBC) và AN ⊥ (SDC).
