Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B. Chứng minh:
a) Tứ giác ABHM nội tiếp.
b) OA.OB = OH.OM = R2.
c) Tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.
Giải bởi Vietjack
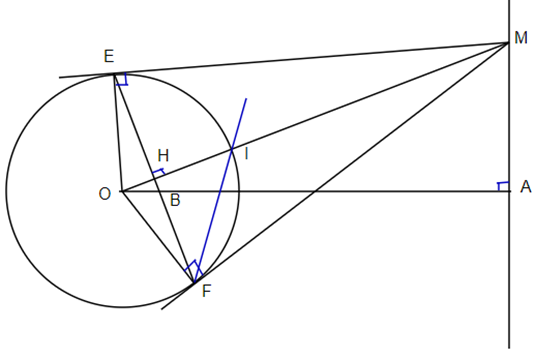
a) Do ME, MF là tiếp tuyến của đường tròn (O) ⇒ EF ⊥ OM.
Tứ giác ABHM có \(\widehat {BHM} = \widehat {MAB} = 90^\circ \) nên tứ giác ABHM là tứ giác nội tiếp đường tròn có bán kính BM.
b) Xét \(\Delta OHB\) và \(\Delta OAM\) có:
\(\widehat O\) chung
\(\widehat {OHB} = \widehat {OAM} = 90^\circ \)
Do đó ∆OHB ᔕ ∆OAM (g.g)
Suy ra \(\frac{{OH}}{{OA}} = \frac{{OB}}{{AM}}\) hay OH.OM = OA.OB (1)
Xét \(\Delta OHE\) và \(\Delta OEM\) có:
\(\widehat O\) chung
\(\widehat {OHE} = \widehat {OEM} = 90^\circ \)
Do đó ∆OHE ᔕ ∆OEM (g.g)
Suy ra \(\frac{{OH}}{{OE}} = \frac{{OE}}{{OM}}\) hay OH.OM = OE2 = R2 (2)
Từ (1) và (2) suy ra OA.OB = OH.OM = R2.
c) Gọi I là giao điểm của OM với đường tròn (O). Nối FI.
Do FI = EI ⇒ \[\Delta EFI\] cân tại I ⇒ \(\widehat {MFI} = \widehat {EFI}\)
⇒ IF là tia phân giác của góc \(\widehat {MFE}\)
mà MI là tia phân giác của góc \(\widehat {EMF}\)
Do đó I là giao điểm của đường phân giác trong của tam giác MEF
⇒ I là tâm đường tròn nội tiếp tam giác MEF
Mà I thuộc đường tròn (O) cố định.
Vậy tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Ta có: \({S_{HBO}} = \frac{1}{2}HO.HB\)
Ta có ∆OHB ᔕ ∆OAM (cmt) suy ra \(\frac{{HB}}{{AM}} = \frac{{OB}}{{OM}}\)
Hay HB.OM = AM.OB (3)
Mà OH.OM = R2 (4)
Nhân (3) và (4) theo vế với vế, ta được:
OH.HB.OM2 = R2.AM.OB = \({R^2}.AM.\frac{{{R^2}}}{{OA}}\)
⇒ \(OH.HB = {R^4}.\frac{{AM}}{{OA.O{M^2}}} = {R^4}.\frac{{AM}}{{OA\left( {O{A^2} + A{M^2}} \right)}}\)
Áp dụng BDT Cô – si ta có: \(O{A^2} + A{M^2} \ge 2.OA.AM\)
Dấu “=” xảy ra khi và chỉ khi OA = AM
⇒ \(OH.HB \le \frac{{{R^4}}}{{OA.2.OA.OM}} = \frac{{{R^4}}}{{2O{A^2}}}\)
⇒ \({S_{\max }} = \frac{{{R^4}}}{{4O{A^2}}}\) ⇔ OA = AM.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn quả, tính xác suất sao cho:
a) Bốn quả lấy ra cùng màu;
b) Có ít nhất một quả màu trắng.
Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm). Qua C thuộc tia Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.
a) Chứng minh: tứ giác AOHC nội tiếp.
b) Chứng minh: AC.AE = AD.CE.
c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh: AM // BN.
Cho nửa đường tròn (O; R) đường kính AB. Bán kính OC vuông góc với AB. Gọi d là tiếp tuyến tại A của nửa đường tròn (O). Qua điểm M bất kì thuộc nửa đường tròn (O), kẻ tiếp tuyến với đường tròn cắt d tại E và cắt đường thẳng OC tại D. Gọi F là giao điểm của BD và d. Tiếp tuyến tại B cắt ED tại K. Chứng minh BK = EF.
Cho đa thức bậc ba P(x) thỏa mãn: P(x) chia cho x2 + 2 dư 2x − 1, chia cho x2 + x dư 16x − 11. Tính P(100).
Tổng tất cả các giá trị thực của tham số m để hàm số y = 3x3 + 2(m + 1)x2 – 3mx + m – 5 có hai điểm cực trị x1, x2 đồng thời y(x1).y(x2) = 0 là
Xác định hàm số bậc hai y = 2x2 + bx + c biết đồ thị của nó có đỉnh I(−1; −2).
Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \(z.\overline z = 1\) là
Cho đa thức bậc 2 có dạng P(x) = ax2 + bx + c biết rằng P(x) thỏa mãn 2 điều kiện sau: P(0) = −2 và 4P(x) – P(2x – 1) = 6x – 6. Chứng minh rằng a + b + c = 0 và xác định đa thức P(x).
Cho một đa giác đều n đỉnh, n ∈ ℕ, n ≥ 3. Tìm n biết rằng đa giác đã cho có 27 đường chéo.
Tìm điểm cố định mà đường thẳng y = (m – 2)x + 3 luôn đi qua với mọi giá trị của m.
Cho tam giác ABC nội tiếp đường tròn tâm O, hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF.
a) Tứ giác BFCH là hình gì?
b) Gọi M là trung điểm của BC. Chứng minh 3 điểm H; M; F thẳng hàng.
c) Chứng minh \(OM = \frac{1}{2}AH.\)
Nếu gửi tiết kiệm theo kì hạn là 12 tháng thì lãi suất hàng tháng là 0,7%. Hỏi 1 người gửi 50 000 000 đồng trong 1 năm thì thu được bao nhiêu tiền lãi? (Tiền lãi của tháng không được cộng vào tiền gửi).
Xác định hàm số bậc hai y = ax2 + bx + c biết đồ thị của nó có đỉnh I(1; −1) và đi qua điểm A(2; 0)
Cho tam giác ABC. Trên tia đối của tia AB, AC lần lượt lấy các điểm D và E sao cho AD = AB và AE = AC. Gọi M, N lần lượt là trung điểm của BC và DE. Chứng minh:
a) \[\Delta ABC = \Delta ADE\].
b) DE = BC và DE // BC.
c) \[\Delta AEN = \Delta ACM\].
d) M, A, N thẳng hàng.
Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB.
a) Chứng minh \(\widehat {ABD} = \widehat {AED}\).
b) Tia ED cắt AB tại F. Chứng minh AC = AF.
c) Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh DI = 2IH.
