Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 75)
-
1325 lượt thi
-
66 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho hình chữ nhật ABCD có M là điểm thuộc cạnh AB sao cho \(AM = \frac{1}{4}AB = 3cm.\) Tìm điểm N trên cạnh DC sao cho diện tích hình MBCN gấp đôi diện tích hình MNDA.
 Xem đáp án
Xem đáp án
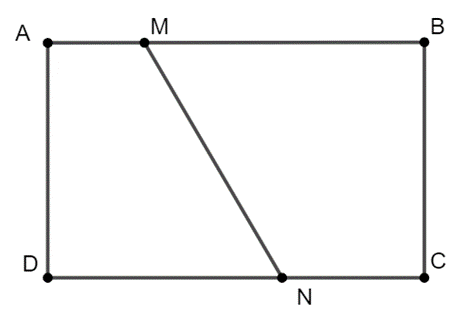
• Vì ABCD là hình chữ nhật ⇒ \(\left\{ {\begin{array}{*{20}{c}}{AB\parallel CD;BC\parallel AD}\\{AB = CD;BC = AD}\end{array}} \right..\)
• Vì AM // CN ⇒ MNDA là hình thang.
• Vì BM // ND ⇒ MBCN là hình thang.
Ta có \(AM = \frac{1}{4}AB = 3cm\) ⇒ AB = 12cm.
Ta có \({S_{MBCN}} = \frac{1}{2}BC\left( {CN + MB} \right);{S_{MNDA}} = \frac{1}{2}AD\left( {AM + DN} \right).\)
Vì diện tích hình thang MBCN gấp đôi diện tích hình thang MNDA
⇒ \({S_{MBCN}} = 2{S_{MNDA}}\)
⇔ \(\frac{1}{2}BC\left( {CN + MB} \right) = 2.\frac{1}{2}AD\left( {AM + DN} \right)\)
⇔ BC(CN + MB) = 2AD(AM + DN)
⇔ CN + MB = 2(AM + DN) (vì BC = AD)
⇔ CD – DN + AB – AM = 2AM + 2DN
⇔ 2AB = 3AM + 3DN
⇔ 2.12 = 3.3 + 3DN
⇔ 3DN = 15
⇔ DN = 5 cm.
Vậy để diện tích hình MBCN gấp đôi diện tích hình MNDA thì điểm N thuộc cạnh DC sao cho DN = 5 cm.
Câu 2:
Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho \(AM = \frac{{AC}}{4},\) N là trung điểm của đoạn thẳng DC. Tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
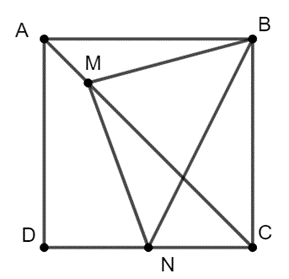
Đặt \(\overrightarrow {AB} = \vec x;\,\,\overrightarrow {AD} = \vec y\)
Vì ABCD là hình vuông nên AB và AD vuông góc với nhau và AB = AD
⇒ \(\vec x.\vec y = 0;\,\,{\vec x^2} = {\vec y^2}\)
Khi đó:
\(\overrightarrow {MB} = \overrightarrow {AB} - \overrightarrow {AM} = \frac{1}{4}\left( {3\vec x - \vec y} \right);\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \frac{1}{4}\left( {\vec x + 3\vec y} \right)\)
Ta có: \(\overrightarrow {MB} .\overrightarrow {MN} = \frac{1}{{16}}\left( {3\vec x - \vec y} \right)\left( {\vec x + 3\vec y} \right)\)
\( = \frac{1}{{16}}\left( {3{{\vec x}^2} - 3{{\vec y}^2} + 8\vec x.\vec y} \right) = 0\)
Mặt khác:
\({\overrightarrow {MB} ^2} = \frac{1}{{16}}{\left( {3\vec x - \vec y} \right)^2} = \frac{5}{8}{\vec y^2};{\overrightarrow {MN} ^2} = \frac{1}{{16}}{\left( {\vec x + 3\vec y} \right)^2} = \frac{5}{8}{\vec y^2}.\)
Vậy tam giác BMN vuông cân tại M.
Câu 3:
Cho nửa đường tròn (O; R) đường kính AB. Bán kính OC vuông góc với AB. Gọi d là tiếp tuyến tại A của nửa đường tròn (O). Qua điểm M bất kì thuộc nửa đường tròn (O), kẻ tiếp tuyến với đường tròn cắt d tại E và cắt đường thẳng OC tại D. Gọi F là giao điểm của BD và d. Tiếp tuyến tại B cắt ED tại K. Chứng minh BK = EF.
 Xem đáp án
Xem đáp án
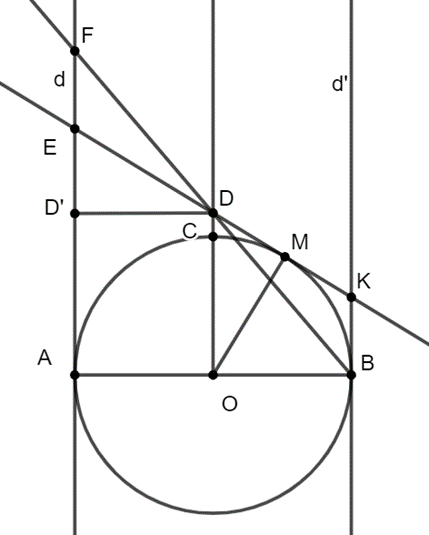
Kẻ DD’ ⊥ d (D’ ∈ d)
Ta có: OC // d (do cùng vuông góc với AB)
⇒ \(\widehat {DFD'} = \widehat {BDO}\)
Xét \(\Delta D'DF\) và \(\Delta OBD\) có:
\(\widehat {FD'D} = \widehat {DOB}\left( { = 90^\circ } \right)\)
D’D = OB \(\left( { = \frac{1}{2}AB} \right)\)
\(\widehat {DFD'} = \widehat {BDO}\)
⇒ \(\Delta D'DF = \Delta OBD\left( {g.c.g} \right)\)
⇒ DB = DF (2 cạnh tương ứng)
Xét \(\Delta DKB\) và \(\Delta DEF\) có:
\(\widehat {KDB} = \widehat {EDF}\)(đối đỉnh)
DB = DF (cmt)
\(\widehat {KBD} = \widehat {EFD}\) (góc so le trong do BK // d)
Do đó \(\Delta DKB = \Delta DEF\left( {g.c.g} \right)\)
⇒ BK = EF (2 cạnh tương ứng)(đpcm).
Câu 4:
Cho đa thức bậc ba P(x) thỏa mãn: P(x) chia cho x2 + 2 dư 2x − 1, chia cho x2 + x dư 16x − 11. Tính P(100).
 Xem đáp án
Xem đáp án
Ta có: P(x) chia cho x2 + 2 dư 2x – 1
⇒ P(x) = Q(x).(x2 + 2) + 2x – 1 (với Q(x) là đa thức bậc nhất)
⇒ P(x) = (ax + b)(x2 + 2) + 2x – 1
Vì P(x) chia x2 + x dư 16x – 11
⇒ P(x) – 16x + 11 chia hết cho x2 + x.
Đặt R(x) = P(x) – 16x + 11
Khi đó R(x) = (ax + b)(x2 + 2) – 14x + 10 chia hết cho x2 + x
Vì thế hai nghiệm x = 0 và x = −1 của x2 + x cũng là nghiệm của R(x), tức là:
\(\left\{ {\begin{array}{*{20}{c}}{\left( {a.0 + b} \right)\left( {0 + 2} \right) - 14.0 + 10 = 0}\\{\left( { - a + b} \right)\left( {1 + 2} \right) - 14.\left( { - 1} \right) + 10 = 0}\end{array}} \right.\)
⇔ \(\left\{ {\begin{array}{*{20}{c}}{a = 3}\\{b = - 5}\end{array}} \right.\)
⇒ P(x) = (3x – 5)(x2 + 2) + 2x – 1
Vậy P(100) = 2905789.
Câu 5:
Cho đa thức bậc 2 có dạng P(x) = ax2 + bx + c biết rằng P(x) thỏa mãn 2 điều kiện sau: P(0) = −2 và 4P(x) – P(2x – 1) = 6x – 6. Chứng minh rằng a + b + c = 0 và xác định đa thức P(x).
 Xem đáp án
Xem đáp án
Ta có P(0) = −2 ⇒ a.0 + b.0 + c = −2 ⇒ c = −2
Ta có 4P(x) – P(2x – 1) = 6x – 6
⇔ 4(ax2 + bx + c) – [a(2x – 1)2 + b(2x – 1) + c] = 6x – 6
⇔ 4ax2 + 4bx + 4c – a(4x2 – 4x + 1) – 2bx + b – c = 6x – 6
⇔ 4ax2 + 4bx + 4c – 4ax2 + 4ax – a – 2bx + b – c = 6x – 6
⇔ 4ax + 2bx + (−a + b + 3c) = 6x – 6
⇔ (4a + 2b)x + (−a + b + 3c) = 6x – 6
⇔ \(\left\{ {\begin{array}{*{20}{c}}{4a + 2b = 6}\\{ - a + b + 3c = - 6}\end{array}} \right.\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{4a + 2b = 6}\\{ - a + b = - 6 - 3.\left( { - 2} \right)}\end{array}} \right.\)
⇔ \(\left\{ {\begin{array}{*{20}{c}}{4a + 2b = 6}\\{ - a + b = 0}\end{array}} \right.\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = 1}\end{array}} \right.\)
Ta có: a + b + c = 1 + 1 + (−2) = 0 (đpcm)
Vậy P(x) = x2 + x – 2.
Câu 6:
Cho tam giác ABC nội tiếp đường tròn tâm O, hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF.
a) Tứ giác BFCH là hình gì?
b) Gọi M là trung điểm của BC. Chứng minh 3 điểm H; M; F thẳng hàng.
c) Chứng minh \(OM = \frac{1}{2}AH.\)
 Xem đáp án
Xem đáp án
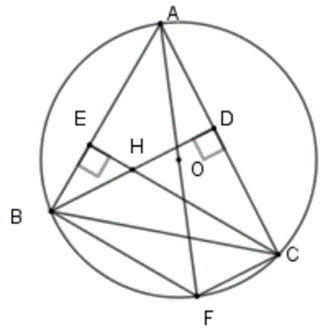
a) \(\widehat {ACF} = 90^\circ \)(chắn nửa đường tròn)
⇒ FC vuông góc với AC
Lại có BH vuông góc với AC
⇒ FC // BH (1)
Chứng minh tương tự: BF // CH (2)
Từ (1) và (2) ⇒ BFCH là hình bình hành.
b) Vì BFCH là hình bình hành nên 2 đường chéo HF và BC giao nhau tại trung điểm mỗi đường.
Mà M là trung điểm của BC ⇒ M đồng thời là trung điểm của HF
⇒ H, M, F thẳng hàng (đpcm)
c) Xét tam giác AHF có O là trung điểm của AF
Có M là trung điểm của HF ⇒ OM là đường trung điểm của tam giác AHF
⇒ \(OM = \frac{1}{2}AH\) (đpcm)
Câu 7:
Cho tam giác ABC, trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC. Một đường thẳng đi qua A cắt các cạnh DE và BC theo thứ tự ở M và N. Chứng minh:
a) BC // DE.
b) AM = AN.
 Xem đáp án
Xem đáp án
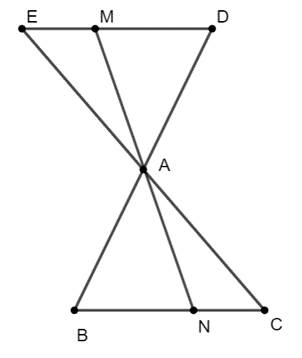
a) Xét \(\Delta ADE\) và \(\Delta ABC\) có:
AD = AB
\(\widehat {DAE} = \widehat {BAC}\) (2 góc đối đỉnh)
AC = AE
⇒ \(\Delta ADE = \Delta BAC\left( {c.g.c} \right)\)
⇒ \(\widehat {ADE} = \widehat {ABC}\) (2 góc tương ứng) mà chúng ở vị trí so le trong với nhau
⇒ BC // DE (đpcm)
b) Xét \(\Delta DAM\) và \(\Delta BAN\) có:
\(\widehat {DAM} = \widehat {BAN}\) (2 góc đối đỉnh)
AD = AB
\(\widehat {ABN} = \widehat {ADM}\) (CMT)
⇒ \(\Delta DAM = \Delta BAN\left( {g.c.g} \right)\)
⇒ AM = AN (2 cạnh tương ứng) (dpcm)
Câu 8:
Cho tam giác ABC. Trên tia đối của tia AB, AC lần lượt lấy các điểm D và E sao cho AD = AB và AE = AC. Gọi M, N lần lượt là trung điểm của BC và DE. Chứng minh:
a) \[\Delta ABC = \Delta ADE\].
b) DE = BC và DE // BC.
c) \[\Delta AEN = \Delta ACM\].
d) M, A, N thẳng hàng.
 Xem đáp án
Xem đáp án
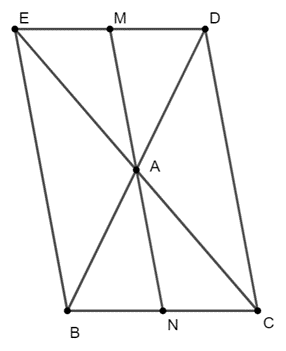
a) Xét ΔABC và ΔADE có:
AB = AD
\(\widehat {BAC} = \widehat {DAE}\) (hai góc đối đỉnh)
AC = AE
Do đó \[\Delta ABC = \Delta ADE\left( {c.g.c} \right)\] (đpcm)
b) Vì \[\Delta ABC = \Delta ADE\] (cmt)
⇒ BC = DE (hai cạnh tương ứng), \[\widehat {ACB} = \widehat {AED}\](hai góc tương ứng).
Mặt khác \(\widehat {ACB},\widehat {AED}\) là hai góc ở vị trí so le trong.
⇒ DE // BC
Vậy DE = BC và DE song song với BC.
c) Ta có: \(EN = \frac{{DE}}{2};MC = \frac{{BC}}{2};DE = BC\) nên EN = MC
Xét \[\Delta AEN\] và \(\Delta ACM\) có:
AE = AC
\(\widehat {NEA} = \widehat {MCA}\) (do \(\widehat {AED} = \widehat {ACB}\))
EN = CM (cmt)
⇒ \[\Delta AEN = \Delta ACM\left( {c.g.c} \right)\] (đpcm)
d) Do \[\Delta AEN = \Delta ACM\] (cmt)
⇒ \(\widehat {NAE} = \widehat {MAC}\) (hai góc tương ứng)
Ta có: \(\widehat {NAM} = \widehat {NAE} + \widehat {EAM} = \widehat {MAC} + \widehat {EAM}\)
mà \(\widehat {MAC} + \widehat {EAM} = \widehat {EAC} = {180^o}\) (hai góc kề bù)
Do đó \(\widehat {NAM} = {180^o}\)
Vậy ba điểm M, A, N thẳng hàng.
Câu 9:
Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB.
a) Chứng minh \(\widehat {ABD} = \widehat {AED}\).
b) Tia ED cắt AB tại F. Chứng minh AC = AF.
c) Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh DI = 2IH.
 Xem đáp án
Xem đáp án
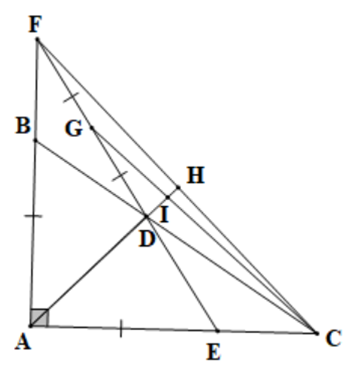
a) Xét \(\Delta ABD\) và \(\Delta EAD\) có:
AB = AE
\(\widehat {BAD} = \widehat {EAD}\) (do AD là tia phân giác của góc BAC)
AD là cạnh chung
Do đó \(\Delta ABD = \Delta AED\left( {c.g.c} \right)\)
Suy ra \(\widehat {ABD} = \widehat {AED}\) (2 góc tương ứng)
b) Xét \(\Delta ABC\) và \(\Delta AEF\) có:
\(\widehat {FAC}\) là góc chung
AB = AE
\(\widehat {ABC} = \widehat {AEF}\) (do \(\widehat {ABD} = \widehat {AED}\))
Do đó \(\Delta ABC = \Delta AEF\left( {g.c.g} \right)\)
Suy ra AC = AF (hai cạnh tương ứng)
c) Xét \(\Delta AHF\) và \(\Delta AHC\) có:
AH là cạnh chung
\(\widehat {FAH} = \widehat {CAH}\) (do AD là tia phân giác của góc BAC)
AF = AC (cmt)
Do đó \(\Delta AHF = \Delta AHC\left( {c.g.c} \right)\)
Suy ra HF = HC (hai cạnh tương ứng)
Khi đó H là trung điểm của FC nên DH là đường trung tuyến xuất phát từ đỉnh D của \(\Delta DFC.\)
Xét \(\Delta DFC\) có CG và DH là hai đường trung tuyến, CG và DH cắt nhau tại I
Suy ra I là trọng tâm của tam giác DFC.
Do đó \(IH = \frac{1}{2}ID\) (tính chất trọng tâm của tam giác)
Hay DI = 2IH.
Vậy DI = 2IH.
Câu 10:
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc AC, từ B kẻ tia By song song AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường thẳng MP cắt AC tại Q và đường thẳng BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
b) Chứng minh CH vuông góc AB.
c) Chứng minh tam giác PIQ cân.
 Xem đáp án
Xem đáp án
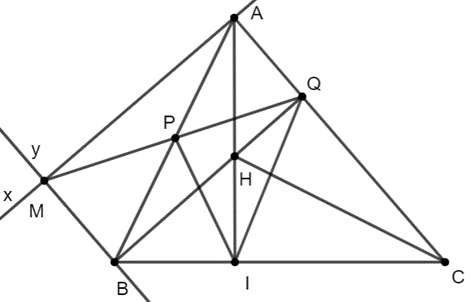
Vì Ax ⊥ AC ⇒ AM ⊥ AC
mà BM // AC
⇒ AM ⊥ BM
Chứng minh tương tự ⇒ AQ // BM và BM // AQ (cmt)
Suy ra AMBQ là hình bình hành.
Mà \(\widehat {AMB} = \widehat {MBQ} = \widehat {ABQ} = \widehat {MAQ} = {90^o}\).
Vậy AMBQ là hình chữ nhật.
b) BQ ⊥ AC (cmt) mà \(BQ \cap AI = H\)
Suy ra H là trực tâm của tam giác ABC.
Do đó: CH ⊥ AB
c) AMBQ là hình chữ nhật mà \(AB \cap QM = P\)
⇒ P là trung điểm AB và P là trung điểm QM
\(\Delta ABI\) vuông tại I có đường trung tuyến IP
⇒ \(IP = \frac{1}{2}AB\)
⇒ IP = PQ
⇒ \(\Delta IPQ\) cân tại P.
Câu 11:
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a) \(\Delta AMB = \Delta EMC\).
b) AC ⊥ CE.
c) BC = 2AM.
 Xem đáp án
Xem đáp án
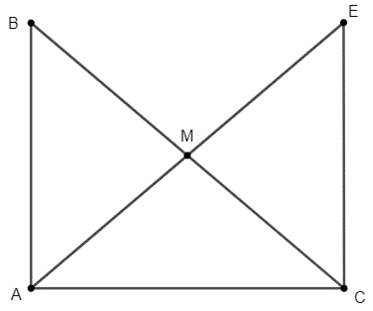
a) Xét \(\Delta ABM\) và \(\Delta ECM\) có:
BM = CM (do M là trung điểm BC)
\(\widehat {AMB} = \widehat {EMC}\) (đối đỉnh)
AM = ME
Do đó \(\Delta ABM = \Delta ECM\left( {c.g.c} \right)\)
b) Ta có: \(\Delta ABM = \Delta ECM\)
⇒ \(\widehat {BAM} = \widehat {CEM}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong của AB và CE
⇒ AB // CE
mà AB ⊥ AC (do \(\Delta ABC\) vuông tại A)
⇒ CE ⊥ AC
c) Xét \(\Delta ABC\) vuông tại A có AM là trung tuyến
⇒ \(AM = BM = CM = \frac{{BC}}{2}\).
⇒ BC = 2AM.
Câu 12:
Cho tam giác ABC đều cạnh a. Gọi M, N là các điểm sao cho \(3\overrightarrow {BM} = 2\overrightarrow {BC} ,5\overrightarrow {AN} = 4\overrightarrow {AC} .\)
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} ,\,\,\overrightarrow {BC} .\overrightarrow {AC} .\)
b) Chứng minh AM vuông góc với BN.
 Xem đáp án
Xem đáp án
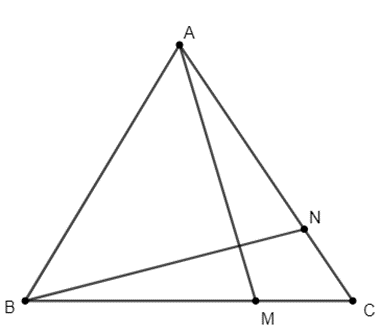
a) Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = a.a.\cos 60^\circ = \frac{{{a^2}}}{2};\)
\(\overrightarrow {BC} .\overrightarrow {AC} = \overrightarrow {CB} .\overrightarrow {CA} = CB.CA.\cos \widehat {BCA} = a.a.\cos 60^\circ = \frac{{{a^2}}}{2}.\)
b) Ta có: \(3\overrightarrow {BM} = 2\overrightarrow {BC} \)
⇔ \(3\left( {\overrightarrow {AM} - \overrightarrow {AB} } \right) = 2\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\)
⇔ \(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AB} \)
Ta có: \(5\overrightarrow {AN} = 4\overrightarrow {AC} \)
⇔ \(5\left( {\overrightarrow {BN} - \overrightarrow {BA} } \right) = 4\overrightarrow {AC} \)
⇔ \(\overrightarrow {BN} = - \overrightarrow {AB} + \frac{4}{5}\overrightarrow {AC} \)
Ta có: \(\overrightarrow {AM} .\overrightarrow {BN} = \left( {\frac{2}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AB} } \right)\left( { - \overrightarrow {AB} + \frac{4}{5}\overrightarrow {AC} } \right)\)
\( = - \frac{2}{3}\overrightarrow {AC} .\overrightarrow {AB} + \frac{8}{{15}}{\overrightarrow {AC} ^2} - \frac{1}{3}{\overrightarrow {AB} ^2} + \frac{4}{{15}}\overrightarrow {AC} .\overrightarrow {AB} \)
\( = - \frac{2}{5}\overrightarrow {AC} .\overrightarrow {AB} + \frac{8}{{15}}{\overrightarrow {AC} ^2} - \frac{1}{3}{\overrightarrow {AB} ^2}\)
\( = - \frac{2}{3}.\frac{{{a^2}}}{2} + \frac{8}{{15}}{a^2} - \frac{1}{3}{a^2} = 0\)
⇒ AM ⊥ BN ⇒ AM vuông góc với BN.
Câu 13:
Từ một điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB đến đường tròn (A, B là hai tiếp điểm). Qua A vẽ đường thẳng song song với MB, cắt đường tròn tại E, đoạn thẳng ME cắt đường tròn tại F. Hai đường thẳng AF và MB cắt nhau tại I.
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
b) Chứng minh \(I{B^2} = IF.IA.\)
c) Chứng minh IB = IM.
 Xem đáp án
Xem đáp án
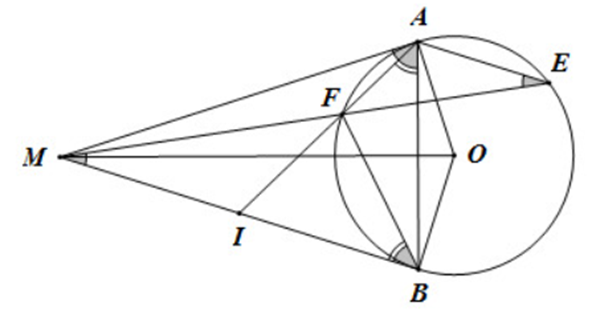
a) Vì MA, MB là tiếp tuyến của (O) nên MA ⊥ AO, MB ⊥ BO.
⇒ \(\widehat {MAO} = \widehat {MBO} = 90^\circ \)
⇒ \(\widehat {MAO} + \widehat {MBO} = 180^\circ \)
⇒ MAOB là tứ giác nội tiếp đường tròn (dpcm)
b) Ta có: \(\widehat {FAB} = \widehat {FBI}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BF)
Xét \(\Delta IAB\) và \(\Delta IBF\) có:
\(\widehat {IAB} = \widehat {IBF}\left( {cmt} \right)\)
\(\widehat {AIB}\) chung
Do đó \(\Delta IAB\) ᔕ \(\Delta IBF\left( {g.g} \right)\)
Suy ra \(\frac{{IA}}{{IB}} = \frac{{IB}}{{IF}}\) hay IB2 = IA.IF.
c) Ta có: \(\widehat {MAI} = \widehat {AEF}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AF)
Vì AE // MB nên \(\widehat {AEF} = \widehat {FMI}\)
Suy ra \(\widehat {MAI} = \widehat {FMI}\)
Xét \(\Delta MAI\) và \(\Delta FMI\) có:
\(\widehat {MAI} = \widehat {FMI}\,\,\left( {cmt} \right)\)
\(\widehat {MIA}\) chung
Do đó \(\Delta MAI\) ᔕ \(\Delta FMI\,\,\left( {g.g} \right)\)
Suy ra \(\frac{{MI}}{{FI}} = \frac{{AI}}{{MI}}\) hay IM2 = IA.IF.
Kết hợp với ý b ta có IB2 = IM2 = IA.IF ⇒ IB = IM (dpcm)
Câu 14:
Chứng minh rằng n(n + 1)(2n + 1) chia hết cho 6 với n thuộc mọi số tự nhiên.
 Xem đáp án
Xem đáp án
Ta có: n(n + 1)(2n + 1)
= n(n + 1)(2n + 2 – 1)
= n(n + 1)(n + 2 + n – 1)
= n(n + 1)(n + 2) + n(n + 1)(n – 1)
Vì n; n + 1; n + 2 là 3 số tự nhiên liên tiếp và n – 1; n; n + 1 cũng là 3 số tự nhiên liên tiếp.
Ta có: 3 số tự nhiên liên tiếp chắc chắn có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2. Do đó, tích 3 số tự nhiên liên tiếp chia hết cho 3.
Vì 3 số tự nhiên liên tiếp luôn có 2 chẵn 1 lẻ hoặc 2 lẻ 1 chẵn. Do đó, tích 3 số tự nhiên liên tiếp cũng chia hết cho 2.
Vì tích 3 số tự nhiên liên tiếp vừa chia hết cho 2 vừa chia hết cho 3 nên chia hết cho 6.
Vậy n(n + 1)(2n + 1) chia hết cho 6 với n thuộc mọi số tự nhiên.
Câu 15:
Cúc đang làm một phép tính mà khi nhân 342 với 1 số có 2 chữ số giống nhau, Cúc đã đặt các tích riêng thẳng cột như trong phép cộng nên Cúc đã tìm ra kết quả ít hơn tích đúng là 12312. Tìm số có 2 chữ số giống nhau đó.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là \(\overline {aa} \) (0 < a < 10; a ∈ ℕ*)
Ta có: \(\overline {aa} = 11a\)
Khi nhân 342 với \(\overline {aa} \) mà đặt các tích riêng thẳng hàng thì tức là ta nhân 342 với lần lượt a và a.
Ta sẽ có: (342\(\overline {aa} \)) – (342.a.2) = 12312
⇔ 342.a.11 – 342.a.2 = 12312
⇔ 342.a.(11 – 2) = 12312
⇔ 342.a.9 = 12312
⇔ 342.a = 1368
⇔ a = 4 (thỏa mãn)
Vậy số cần tìm là 44.
Câu 16:
Chứng minh rằng với mọi số nguyên n thì n7 – n chia hết cho 7.
 Xem đáp án
Xem đáp án
Đặt An = n7 – n.
Khi n = 1 thì A1 = 0 và chia hết cho 7.
Giả sử đã có Ak = (k7 – k) ⋮ 7 (giả thiết quy nạp)
Ta phải chứng minh Ak + 1 ⋮ 7, tức là (k + 1)7 – (k + 1) ⋮ 7.
Áp dụng công thức Nhị thức Niu – tơn ta có:
Ak + 1 = (k + 1)7 – (k + 1)
= k7 + 7k6 + 21k5 + 35k4 + 35k3 + 21k2 + 7k + 1 – k – 1
= k7 – k + 7(k6 + 3k5 + 5k4 + 5k3 +3k2 + k).
Theo giả thiết quy nạp thì Ak = k7 – k chia hết cho 7, do đó Ak + 1 ⋮ 7.
Vậy n7 – n chia hết cho 7 với mọi số nguyên n.
Câu 17:
Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn quả, tính xác suất sao cho:
a) Bốn quả lấy ra cùng màu;
b) Có ít nhất một quả màu trắng.
 Xem đáp án
Xem đáp án
Không gian mẫu là kết quả việc chọn ngẫu nhiên 4 quả cầu từ hộp 10 quả cầu.
⇒ \(n\left( \Omega \right) = C_{10}^4 = 210\)
a) A: “ Bốn quả lấy ra cùng màu”
TH1: Bốn quả lấy ra cùng đen
⇒ Có \(C_4^4 = 1\) cách.
TH2: Bốn quả lấy ra cùng trắng
⇒ Có \(C_6^4 = 15\) cách.
⇒ \(n\left( A \right) = 1 + 15 = 16.\)
⇒ \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{16}}{{210}} = \frac{8}{{105}}.\]
b. B: “ Cả 4 quả lấy ra đều màu đen”
⇒ \(\overline B \): “ Có ít nhất 1 quả màu trắng”.
Ta có: \(n\left( B \right) = C_4^4 = 1.\)
⇒ \(P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{1}{{210}}.\)
⇒ \(P\left( {\overline B } \right) = 1 - P\left( B \right) = 1 - \frac{1}{{210}} = \frac{{209}}{{210}}.\)
Câu 18:
Cho phương trình sau: x2 + ax + b = 0. Xác định a và b để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn: x1 – x2 = 5 và \({x_1}^3 - {x_2}^3 = 35.\) Tìm 2 nghiệm phân biệt đó.
 Xem đáp án
Xem đáp án
Để phương trình có 2 nghiệm phân biệt thì \(\Delta > 0\) ⇔ a2 – 4b > 0
Theo hệ thức Viet, ta có:
\(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = - a}\\{{x_1}.{x_2} = b}\end{array}} \right.\)
Ta có: \({x_1}^3 - {x_2}^3 = 35\)
⇔ \(\left( {{x_1} - {x_2}} \right)\left( {{x_1}^2 + {x_1}{x_2} + {x_2}^2} \right) = 35\)
⇔ \(5\left( {{x_1}^2 + {x_1}{x_2} + {x_2}^2} \right) = 35\)
⇔ \({x_1}^2 + {x_1}{x_2} + {x_2}^2 = 7\)
⇔ \({\left( {{x_1} - {x_2}} \right)^2} + 3{x_1}{x_2} = 7\)
⇔ \(25 + 3{x_1}{x_2} = 7\)
⇔ \({x_1}{x_2} = - 6\)
⇔ b = −6
Ta có hệ phương trình sau:
\(\left\{ {\begin{array}{*{20}{c}}{{x_1} - {x_2} = 5}\\{{x_1}{x_2} = - 6}\end{array}} \right.\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{\left( {5 + {x_2}} \right){x_2} = - 6}\end{array}} \right.\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{{x_2}^2 + 5{x_2} + 6 = 0}\end{array}} \right.\)
⇔ \(\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{\left( {{x_2} + 2} \right)\left( {{x_2} + 3} \right) = 0}\end{array}} \right.\)
⇔ \(\left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{{x_2} + 2 = 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{{x_2} + 3 = 0}\end{array}} \right.}\end{array}} \right.\) ⇔ \(\left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x_1} = 3}\\{{x_2} = - 2}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{x_1} = 2}\\{{x_2} = - 3}\end{array}} \right.}\end{array}} \right.\)
TH1: x1 = 3 và x2 = −2 ⇒ x1 + x2 = 1 = a
⇒ \(\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = - 6}\end{array}} \right.\)
TH2: x1 = 2 và x2 = −3 ⇒ x1 + x2 = −1 = a
⇒ \(\left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = - 6}\end{array}} \right.\)
Vậy các cặp (a,b) thỏa mãn là (1,−6) hoặc (−1,−6).
Câu 19:
Bỏ ngoặc rồi tính: 25 – (−17) + 24 – 12.
 Xem đáp án
Xem đáp án
25 – (−17) + 24 – 12
= 25 + 17 + 24 – 12
= 54.
Câu 20:
Tìm x, y là số tự nhiên thỏa mãn phương trình \({2^x} + 3 = {y^2}.\)
 Xem đáp án
Xem đáp án
Xét x = 0 ta có:
\({y^2} = 3 + {2^0} = 4\) ⇔ y = 2 (do y là số tự nhiên)
Xét x = 1 ta có:
\({y^2} = 3 + 2 = 5\) ⇒ Không có nghiệm y là số tự nhiên thỏa mãn
Xét x > 1 ta có:
\({2^x} \ge 4\) ⇒ 2x ⋮ 4
Do đó 2x + 3 chia 4 dư 3, mà y2 là số chính phương chia 4 chỉ dư 0 hoặc 1
⇒ ∀ x > 1, phương trình có nghiệm x, y là số tự nhiên thỏa mãn.
Vậy (x,y) = (0,2) là nghiệm duy nhất.
Câu 21:
Trong không gian Oxyz, cho mặt phẳng (P) : x – 2y + 2z + 6 = 0 và các điểm A(−1; 2; 3), B(3; 0; −1), C(1; 4; 7). Tìm điểm M thuộc (P) sao cho MA2 + MB2 + MC2 đạt giá trị nhỏ nhất.
 Xem đáp án
Xem đáp án
Gọi G là trọng tâm tam giác ABC có tọa độ là G(1; 2; 3).
Ta có: \(M{A^2} + M{B^2} + M{C^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + {\overrightarrow {MC} ^2}\)
\( = {\left( {\overrightarrow {MG} + \overrightarrow {GA} } \right)^2} + {\left( {\overrightarrow {MG} + \overrightarrow {GB} } \right)^2} + {\left( {\overrightarrow {MG} + \overrightarrow {GC} } \right)^2}\)
\( = 3M{G^2} + \left( {G{A^2} + G{B^2} + G{C^2}} \right) + 2\overrightarrow {MG} \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right)\)
\( = 3M{G^2} + \left( {G{A^2} + G{B^2} + G{C^2}} \right)\)
MA2 + MB2 + MC2 đạt giá trị nhỏ nhất ⇔ MG nhỏ nhất (do GA2 + GB2 + GC2 không đổi)
⇔ M là hình chiếu của G trên (P)
Mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n \left( {1; - 2;2} \right).\)
GM vuông góc với (P) nhận vectơ pháp tuyến của (P) làm vectơ chỉ phương.
Phương trình của GM là: \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 - 2t}\\{z = 3 + 2t}\end{array}} \right..\)
Tọa độ của điểm M(1 + t; 2 – 2t; 3 + 2t) thỏa mãn:
(1 + t) – 2(2 – 2t) + 2(3 + 2t) + 6 = 0 ⇔ \(t = - \frac{{11}}{9}.\)
⇒ \(M\left( { - \frac{2}{9};\frac{{40}}{9};\frac{5}{9}} \right).\)
Vậy \(M\left( { - \frac{2}{9};\frac{{40}}{9};\frac{5}{9}} \right)\) thì MA2 + MB2 + MC2 đạt giá trị nhỏ nhất.
Câu 22:
Có bao nhiêu giá trị của m để giá trị lớn nhất của hàm số y = |−x4 + 8x2 + m| trên đoạn [−1; 3] bằng 2018?
 Xem đáp án
Xem đáp án
Xét hàm số y = f(x) = −x4 + 8x2 + m trên đoạn [−1; 3]:
\(y' = f'\left( x \right) = - 4{x^3} + 16x\)
\(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = \pm 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\) (loại x = −2 vì −2 ∉ [−1; 3])
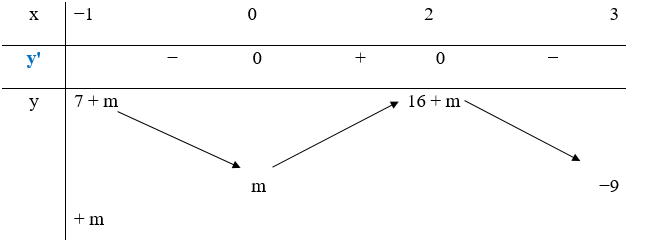
Từ bảng biến thiên hàm số y = f(x) = −x4 + 8x2 + m ta thấy:
\[\mathop {\max }\limits_{\left[ { - 1;\,\,3} \right]} \left| {f\left( x \right)} \right| = \max \left\{ {\left| {7 + m} \right|;\,\,\left| m \right|;\,\,\left| {16 + m} \right|;\,\,\left| { - 9 + m} \right|} \right\} = 2018\]
TH1: \(\mathop {\max }\limits_{\left[ { - 1;\,3} \right]} \left| {f\left( x \right)} \right| = \left| {7 + m} \right| = 2018 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2011}\\{m = - 2025}\end{array}} \right.\)
m = 2011 ⇒ |16 + m| = 2027 > 2018 (loại)
m = −2025 ⇒ |−9 + m| = 2034 > 2018 (loại)
TH2: \(\mathop {\max }\limits_{\left[ { - 1;\,3} \right]} \left| {f\left( x \right)} \right| = \left| m \right| = 2018 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2018}\\{m = - 2018}\end{array}} \right.\) (loại)
TH3: \(\mathop {\max }\limits_{\left[ { - 1;\,3} \right]} \left| {f\left( x \right)} \right| = \left| {16 + m} \right| = 2018 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2002}\\{m = - 2034}\end{array}} \right.\)
m = 2002 (thỏa mãn)
m = −2034 ⇒ |−9 + m| = 2025 > 2018 (loại)
TH4: \(\mathop {\max }\limits_{\left[ { - 1;\,3} \right]} \left| {f\left( x \right)} \right| = \left| { - 9 + m} \right| = 2018 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 2027}\\{m = - 2009}\end{array}} \right.\)
m = 2027 ⇒ |m| = 2027 > 2018 (loại)
m = − 2009 ⇒ |m| = 2009 < 2018 (thỏa mãn)
Vậy có 2 giá trị của m thỏa mãn đề bài.
Câu 23:
Cho hình trụ có bán kính đáy bằng 3 và thể tích bằng 18π. Tính diện tích xung quanh Sxq của hình trụ.
 Xem đáp án
Xem đáp án
Ta có: V = πr2h ⇔ 18π = π32h ⇔ h = 2.
Khi đó Sxq = 2πrh = 12π.
Câu 24:
Cho một đa giác đều n đỉnh, n ∈ ℕ, n ≥ 3. Tìm n biết rằng đa giác đã cho có 27 đường chéo.
 Xem đáp án
Xem đáp án
Với hai đỉnh sẽ cho ta một đoạn thẳng, do đó số đoạn thẳng được tạo ra từ n đỉnh là \(C_n^2.\)
Đa giác có n đỉnh sẽ có n cạnh. Trong số \(C_n^2\) đoạn thẳng có n đoạn thẳng là cạnh của đa giác. Do đó số đường chéo của đa giác là \(C_n^2 - n = \frac{{n\left( {n - 3} \right)}}{2}.\)
Theo đề bài ta có phương trình sau
\(\frac{{n\left( {n - 3} \right)}}{2} = 27 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{n = 9}\\{n = - 6}\end{array}} \right.\)
Do n ∈ ℕ, n ≥ 3 ⇒ n = 9.
Câu 25:
Cho tam giác ABC có A(−5; 6), B(1; −3), C(−1; 1). Tìm tọa độ trung điểm H của BC.
 Xem đáp án
Xem đáp án
Trung điểm H của BC có tọa độ là \(H\left( {\frac{{{x_B} + {x_C}}}{2};\frac{{{y_B} + {y_C}}}{2}} \right)\)
⇔ \(H\left( {\frac{{1 - 1}}{2};\frac{{ - 3 + 1}}{2}} \right)\) ⇔ \(H\left( {0; - 1} \right).\)
Vậy H(0; −1).
Câu 26:
Cho tam giác ABC vuông tại A.
a) Giả sử \(\widehat B = 54^\circ .\) Tính góc C.
b) Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm N sao cho MA = MN. Chứng minh AB // NC.
 Xem đáp án
Xem đáp án
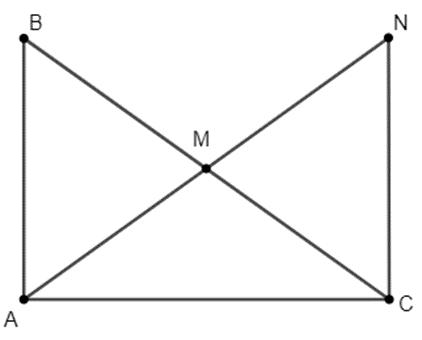
a) Vì tam giác ABC vuông tại A ⇒ \(\widehat {BAC} = 90^\circ .\)
Xét tam giác ABC có:
\(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \)
⇔ \(\widehat {ACB} = 180^\circ - 54^\circ - 90^\circ = 36^\circ \)
b) Xét \(\Delta ABM\) và \(\Delta NCM\) có:
AM = MN
MB = MC (do M là trung điểm BC)
\(\widehat {NMC} = \widehat {AMB}\) (đối đỉnh)
Do đó \(\Delta ABM = \Delta NCM\left( {c.g.c} \right)\)
Suy ra \(\widehat {ABM} = \widehat {NCM}\) (2 góc tương ứng)
Vậy AB // NC (do 2 góc so le trong) (đpcm)
Câu 27:
Cho tam giác ABC vuông tại A (AB < AC) và đường cao AH. Từ H kẻ HE ⊥ AB, HF ⊥ AC (E ∈ AB; F ∈ AC).
a) Chứng minh tứ giác AEHF là hình chữ nhật.
b) Gọi D là điểm đối xứng của A qua F. Chứng minh DHEF là hình bình hành.
c) Gọi I là giao điểm của EF và AH, M là trung điểm của BC. Qua A kẻ tia Ax vuông góc với đường thẳng MI cắt tia CB tại K. Chứng minh 4 điểm K, E, I, F thẳng hàng.
 Xem đáp án
Xem đáp án
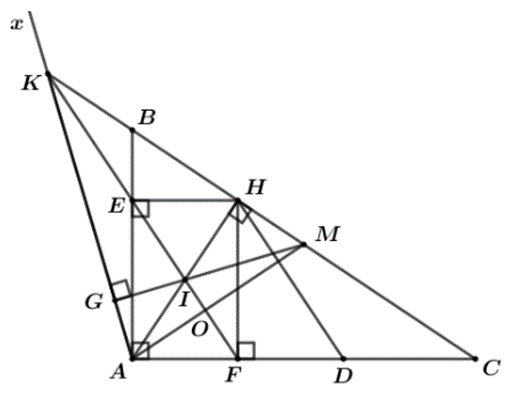
a) Tam giác ABC vuông tại A ⇒ \(\widehat {BAC} = 90^\circ .\)
Vì HE ⊥ AB, HF ⊥ AC nên \(\widehat {HEA} = 90^\circ ,\widehat {HFA} = 90^\circ .\)
Xét tứ giác AEHF có: \(\widehat {EAF} = \widehat {HEA} = \widehat {HFA} = 90^\circ .\)
⇒ Tứ giác AEHF là hình chữ nhật (dấu hiệu nhận biết).
b) Vì AEHF là hình chữ nhật ⇒ EH // AF và EH = AF (tính chất hình chữ nhật)
Vì D là tâm đối xứng của A qua F nên F là trung điểm của AD ⇒ AF = FD.
⇒ EH // FD và EH = FD.
⇒ DHEF là hình bình hành (dấu hiệu nhận biết)
c) Vì I là giao điểm của EF và AH nên ba điểm E, I, F thẳng hàng.
Gọi O là giao điểm của EF và AM.
Vì AM là đường trung tuyến của \(\Delta ABC\) nên AM = MC ⇒ \(\Delta AMC\) cân tại M
⇒ \(\widehat {MAC} = \widehat {MCA}\)
Vì AEHF là hình chữ nhật có I là giao điểm 2 đường chéo ⇒ \(\widehat {IAF} = \widehat {IFA}\)
Xét \(\Delta AHC\) có: \(\widehat {HAC} + \widehat {HCA} = 90^\circ \) hay \(\widehat {IAF} + \widehat {MCA} = 90^\circ \)
⇒ \(\widehat {IAF} + \widehat {MAC} = 90^\circ \) hay \(\widehat {OFA} + \widehat {OAF} = 90^\circ \)
Xét \(\Delta OAF\) có: \[\widehat {OFA} + \widehat {OAF} = 90^\circ \Rightarrow \widehat {AOF} = 90^\circ \]
⇒ EF ⊥ AM tại O hay IF ⊥ AM tại O.
Xét \(\Delta KAM\) có: GM ⊥ KA; AH ⊥ KM.
Mà I là giao điểm của AH và GM nên I là trực tâm của \(\Delta KAM.\)
Suy ra KI ⊥ AM mà IF ⊥ AM.
Do đó K, I, F thẳng hàng.
Ta có:
• Ba điểm E, I, F thẳng hàng.
• Ba điểm K, I, F thẳng hàng.
Do đó bốn điểm I, K, E, F thẳng hàng.
Câu 28:
Cho x, y, z là 3 số thực thay đổi thỏa mãn điều kiện x + y + z = 3. Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{1}{{\sqrt x }} + \frac{1}{{\sqrt y }} + \frac{1}{{\sqrt z }}.\)
 Xem đáp án
Xem đáp án
Áp dụng BDT Cô – si, ta có:
\(P = \frac{1}{{\sqrt x }} + \frac{1}{{\sqrt y }} + \frac{1}{{\sqrt z }} \ge 3\sqrt[3]{{\frac{1}{{\sqrt {xyz} }}}}\)
mà \(\sqrt[3]{{xyz}} \le \frac{{x + y + z}}{3} = 1\)
⇒ P ≥ 3.
Vậy giá trị nhỏ nhất của P = 3 ⇔ x = y = z = 1.
Câu 29:
Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B. Chứng minh:
a) Tứ giác ABHM nội tiếp.
b) OA.OB = OH.OM = R2.
c) Tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.
 Xem đáp án
Xem đáp án
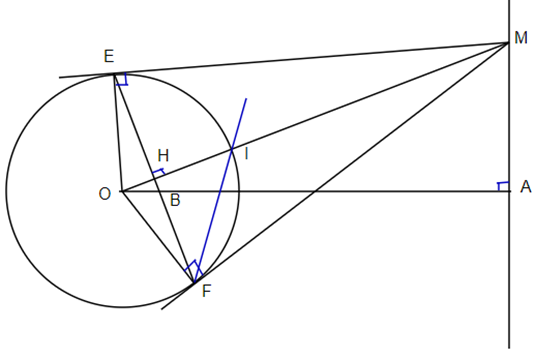
a) Do ME, MF là tiếp tuyến của đường tròn (O) ⇒ EF ⊥ OM.
Tứ giác ABHM có \(\widehat {BHM} = \widehat {MAB} = 90^\circ \) nên tứ giác ABHM là tứ giác nội tiếp đường tròn có bán kính BM.
b) Xét \(\Delta OHB\) và \(\Delta OAM\) có:
\(\widehat O\) chung
\(\widehat {OHB} = \widehat {OAM} = 90^\circ \)
Do đó ∆OHB ᔕ ∆OAM (g.g)
Suy ra \(\frac{{OH}}{{OA}} = \frac{{OB}}{{AM}}\) hay OH.OM = OA.OB (1)
Xét \(\Delta OHE\) và \(\Delta OEM\) có:
\(\widehat O\) chung
\(\widehat {OHE} = \widehat {OEM} = 90^\circ \)
Do đó ∆OHE ᔕ ∆OEM (g.g)
Suy ra \(\frac{{OH}}{{OE}} = \frac{{OE}}{{OM}}\) hay OH.OM = OE2 = R2 (2)
Từ (1) và (2) suy ra OA.OB = OH.OM = R2.
c) Gọi I là giao điểm của OM với đường tròn (O). Nối FI.
Do FI = EI ⇒ \[\Delta EFI\] cân tại I ⇒ \(\widehat {MFI} = \widehat {EFI}\)
⇒ IF là tia phân giác của góc \(\widehat {MFE}\)
mà MI là tia phân giác của góc \(\widehat {EMF}\)
Do đó I là giao điểm của đường phân giác trong của tam giác MEF
⇒ I là tâm đường tròn nội tiếp tam giác MEF
Mà I thuộc đường tròn (O) cố định.
Vậy tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Ta có: \({S_{HBO}} = \frac{1}{2}HO.HB\)
Ta có ∆OHB ᔕ ∆OAM (cmt) suy ra \(\frac{{HB}}{{AM}} = \frac{{OB}}{{OM}}\)
Hay HB.OM = AM.OB (3)
Mà OH.OM = R2 (4)
Nhân (3) và (4) theo vế với vế, ta được:
OH.HB.OM2 = R2.AM.OB = \({R^2}.AM.\frac{{{R^2}}}{{OA}}\)
⇒ \(OH.HB = {R^4}.\frac{{AM}}{{OA.O{M^2}}} = {R^4}.\frac{{AM}}{{OA\left( {O{A^2} + A{M^2}} \right)}}\)
Áp dụng BDT Cô – si ta có: \(O{A^2} + A{M^2} \ge 2.OA.AM\)
Dấu “=” xảy ra khi và chỉ khi OA = AM
⇒ \(OH.HB \le \frac{{{R^4}}}{{OA.2.OA.OM}} = \frac{{{R^4}}}{{2O{A^2}}}\)
⇒ \({S_{\max }} = \frac{{{R^4}}}{{4O{A^2}}}\) ⇔ OA = AM.
Câu 30:
Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm). Qua C thuộc tia Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.
a) Chứng minh: tứ giác AOHC nội tiếp.
b) Chứng minh: AC.AE = AD.CE.
c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh: AM // BN.
 Xem đáp án
Xem đáp án
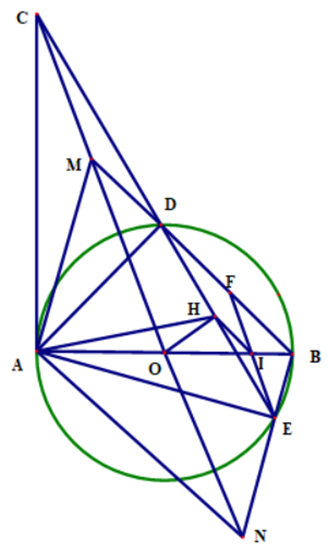
a) Ta có: \(\widehat {CAB} = \widehat {OHC} = 90^\circ \) ⇒ \(\widehat {CAB} + \widehat {OHC} = 180^\circ \).
Do đó tứ giác AHOC nội tiếp.
b) Xét \(\Delta ACD\) và \(\Delta ECA\) có:
\(\widehat {CAD} = \widehat {AEC}\)
\(\widehat {ACE}\) chung
Do đó ∆ACD ᔕ ∆ECA (g.g)
Suy ra \(\frac{{CA}}{{CE}} = \frac{{AD}}{{AE}}\) hay AC.AE = AD.CE.
c) Từ E kẻ đường thẳng song song với MN cắt AB tại I và BD tại F
⇒ \(\widehat {HEI} = \widehat {HCO}\)
Vì tứ giác AOHC nội tiếp ⇒ \(\widehat {HAO} = \widehat {HCO} = \widehat {HEI}\)
Suy ra tứ giác AHIE nội tiếp
⇒ \(\widehat {IHE} = \widehat {IAE} = \widehat {BDE}\)
⇒ IH // BD
mà H là trung điểm của DE
⇒ I là trung điểm của EF
⇒ EF // MN và IE = IF
⇒ O là trung điểm của MN
⇒ Tứ giác AMBN là hình bình hành
⇒ AM // BN (đpcm)
Câu 31:
Làm phép tính sau: 2 357 × 24.
 Xem đáp án
Xem đáp án
2357 × 24 = 2357 × (20 + 4)
= 2357 × 20 + 2357 × 4
= 47 410 + 9 428
= 56 838.
Vậy 2 357 × 24 = 56 838.
Câu 32:
Giải phương trình: \(4\sqrt {x + 1} = {x^2} - 5x + 14.\)
 Xem đáp án
Xem đáp án
Ta có: \(4\sqrt {x + 1} = {x^2} - 5x + 14\) (ĐK: x ≥ −1)
⇔ \(4\sqrt {x + 1} - 8 = {x^2} - 5x + 6\)
⇔ \(4\left( {\sqrt {x + 1} - 2} \right) = {x^2} - 5x + 6\)
⇔ \(\frac{{4\left( {x - 3} \right)}}{{\left( {\sqrt {x + 1} - 2} \right)}} = \left( {x - 2} \right)\left( {x - 3} \right)\)
⇔ \(\left( {x - 3} \right)\left( {\frac{4}{{\sqrt {x + 1} - 2}} - x + 2} \right) = 0\)
⇔ x – 3 = 0
⇔ x = 3 (thỏa mãn)
Vậy phương trình đã cho có nghiệm x = 3.
Câu 33:
Một mảnh đất hình chữ nhật có chiều dài là 38m, chiều rộng bằng \[\frac{3}{4}\] chiều dài, trong đó diện tích đất làm nhà chiếm 25%. Tính:
a) Diện tích của mảnh đất đó.
b) Diện tích đất làm nhà là bao nhiêu mét vuông?
 Xem đáp án
Xem đáp án
a) Chiều rộng mảnh đất là:
\(38 \times \frac{3}{4} = 28,5\) (m)
Diện tích mảnh đất là:
28,5 ´ 38 = 1083 (m2)
b) Diện tích đất làm nhà:
1083 ´ 25% = 270,75 (m2)
Đáp số:
a) 1083 m.
b) 270,75 m2.
Câu 34:
Một mảnh đất hình chữ nhật có chiều dài là 40m, chiều rộng bằng \(\frac{1}{2}\) chiều dài, trong đó diện tích đất làm nhà chiếm 30%. Tính:
a) Diện tích của mảnh đất đó.
b) Diện tích đất làm nhà là bao nhiêu mét vuông?
 Xem đáp án
Xem đáp án
a) Chiều rộng mảnh đất là:
\(40 \times \frac{1}{2} = 20\) (m)
Diện tích mảnh đất là:
20 ´ 40 = 800 (m2)
b) Diện tích đất làm nhà:
800 ´ 30% = 240 (m2)
Đáp số: a) 800 m;
b) 240 m2.
Câu 35:
Tìm số \(\overline {abc} \). Biết \(\overline {abc} \) chia hết cho 45 và \(\overline {abc} - \overline {cba} = 396\) (với c ≠ 0).
 Xem đáp án
Xem đáp án
\(\overline {abc} \) chia hết cho 45 nên \(\overline {abc} \) chia hết cho 5 và 9 nên c = 0 hoặc 5 mà c ≠ 0 nên c = 5.
Ta có: \(\overline {ab5} - \overline {5ba} = 396\)
Ta viết lại biểu thức như sau: \(396 + \overline {5ba} = \overline {ab5} \)
6 + a tận cùng là 5 nên a = 9
Nên ta lại có: \(\overline {abc} = \overline {9b5} \) chia hết cho 9 và 5.
Nên 9 + b + 5 chia hết cho 9, nên b = 4.
Suy ra \(\overline {abc} = 945\)
Câu 36:
Cho \(\overline {abc} + \overline {\deg } \) chia hết cho 37. Chứng minh rằng \(\overline {abc\deg } \) chia hết cho 37.
 Xem đáp án
Xem đáp án
Ta có: \(\overline {abc\deg } = \overline {abc} .1000 + \overline {\deg } = 999.\overline {abc} + \overline {abc} + \overline {\deg } \)
\( = 32.27\overline {abc} + \left( {\overline {abc} + \overline {\deg } } \right)\)
Do \(37.27.\overline {abc} \) chia hết cho 37
⇒ \(\overline {abc\deg } \) chia hết cho 37 với \(\overline {abc} + \overline {\deg } \) chia hết cho 37.
Câu 37:
Cho x, y, z > 0 và xyz = 1. CMR: \(\frac{{{x^2}}}{{\left( {1 + y} \right)}} + \frac{{{y^2}}}{{\left( {1 + z} \right)}} + \frac{{{z^2}}}{{\left( {1 + x} \right)}} \ge \frac{3}{2}\)?
 Xem đáp án
Xem đáp án
Áp dụng BĐT cô-si:
\(\frac{{{x^2}}}{{1 + y}} + \frac{{{y^2}}}{{1 + z}} + \frac{{{z^2}}}{{1 + x}} \ge \frac{{{{\left( {x + y + z} \right)}^2}}}{{1 + y + 1 + z + 1 + x}} = \frac{{{{\left( {x + y + z} \right)}^2}}}{{\left( {x + y + z} \right) + 3}}\)
Áp dụng BĐT cô-si: \(x + y + z \ge 3\sqrt[3]{{xyz}} = 3\)
Do đó: \(\frac{{{x^2}}}{{1 + y}} + \frac{{{y^2}}}{{1 + z}} + \frac{{{z^2}}}{{1 + x}} \ge \frac{{{{\left( {x + y + z} \right)}^2}}}{{\left( {x + y + z} \right) + 3}}\)
\( \ge \frac{{{{\left( {x + y + z} \right)}^2}}}{{\left( {x + y + z} \right) + \left( {x + y + z} \right)}} = \frac{{x + y + z}}{2} \ge \frac{3}{2}\)
Dấu “=” xảy ra khi và chỉ khi x = y = z = 1.
Vậy \(\frac{{{x^2}}}{{\left( {1 + y} \right)}} + \frac{{{y^2}}}{{\left( {1 + z} \right)}} + \frac{{{z^2}}}{{\left( {1 + x} \right)}} \ge \frac{3}{2}\), dấu “=” xảy ra khi và chỉ khi x = y = z = 1.
Câu 38:
Cho x, y, z > 0 và x3 + y3 + z3 = 1. Chứng minh rằng:
\[\frac{{{x^2}}}{{\sqrt {1 - {x^2}} }} + \frac{{{y^2}}}{{\sqrt {1 - {y^2}} }} + \frac{{{z^2}}}{{\sqrt {1 - {z^2}} }} \ge 2\].
 Xem đáp án
Xem đáp án
Theo BĐT cô-si ta có: \(\frac{{{x^2}}}{{\sqrt {1 - {x^2}} }} = \frac{{{x^3}}}{{x\sqrt {1 - {x^2}} }} \ge \frac{{{x^3}}}{{\frac{{{x^2} + 1 - {x^2}}}{2}}} = 2{x^3}\)
Chứng minh tương tự: \(\frac{{{y^2}}}{{\sqrt {1 - {y^2}} }} \ge 2{y^3}\); \(\frac{{{z^2}}}{{\sqrt {1 - {z^2}} }} \ge 2{z^3}\).
Cộng vế với vế các bất đẳng thức trên ta có:
\(\frac{{{x^2}}}{{\sqrt {1 - {x^2}} }} + \frac{{{y^2}}}{{\sqrt {1 - {y^2}} }} + \frac{{{z^2}}}{{\sqrt {1 - {z^2}} }} \ge 2\left( {{x^3} + {y^3} + {z^3}} \right) = 2\) (đpcm)
Câu 39:
Tổng tất cả các giá trị thực của tham số m để hàm số y = 3x3 + 2(m + 1)x2 – 3mx + m – 5 có hai điểm cực trị x1, x2 đồng thời y(x1).y(x2) = 0 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D.
Hàm số y = 3x3 + 2(m + 1)x2 – 3mx + m – 5 có 2 điểm cực trị đồng thời y(x1).y(x2) = 0 khi và chỉ khi phương trình 3x3 + 2(m + 1)x2 – 3mx + m – 5 = 0 (1) có đúng 2 nghiệm phân biệt.
Ta có: 3x3 + 2(m + 1)x2 – 3mx + m – 5 = 0
⇔ (x – 1)[3x2 + (2m + 5)x + 5 – m] = 0
⇔ \[\left[ \begin{array}{l}x = 1\\3{x^2} + (2m + 5)x + 5 - m = 0(*)\end{array} \right.\]
(1) có đúng 2 nghiệm phân biệt khi và chỉ khi:
TH1: (*) có nghiệm kép khác 1.
\( \Rightarrow \left\{ \begin{array}{l}\Delta = {\left( {2m + 5} \right)^2} - 12\left( {5 - m} \right) = 0\\3 + 2m + 5 + 5 - m \ne 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}4{m^2} + 32m - 35 = 0\\m \ne - 13\end{array} \right. \Leftrightarrow m = \frac{{ - 8 \pm 3\sqrt {11} }}{2}\)
TH2: (*) có 2 nghiệm phân biệt trong đó có 1 nghiệm x = 1.
\( \Rightarrow \left\{ \begin{array}{l}\Delta = {\left( {2m + 5} \right)^2} - 12\left( {5 - m} \right)\\3 + 2m + 5 + 5 - m = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}4{m^2} + 32m - 35 > 0\\m = - 13\end{array} \right.\)
⇔ m = −13
Vậy có 3 giá trị m thỏa mãn. Khi đó tổng của các giá trị m là:
\(\frac{{ - 8 + 3\sqrt {11} }}{2} + \frac{{ - 8 - 3\sqrt {11} }}{2} - 13 = - 21\).
Câu 40:
Tìm tập hợp tất cả các giá trị của tham số m để hàm số:
\(y = f\left( x \right) = \sqrt {{x^2} - 3mx + 4} \) có tập xác định là D = ℝ.
 Xem đáp án
Xem đáp án
Hàm số đã cho xác định trên ℝ khi và chỉ khi x2 – 3mx + 4 ≥ 0, \(\forall \)x ∈ ℝ.
⇒ ∆ = 9m2 – 16 ≤ 0
\( \Leftrightarrow {m^2} \le \frac{{16}}{9}\)
\( \Leftrightarrow \frac{{ - 4}}{3} \le m \le \frac{4}{3}\)
Vậy với \(\frac{{ - 4}}{3} \le m \le \frac{4}{3}\) thì thỏa mãn yêu cầu bài toán.
Câu 41:
Để lát nền một căn phòng có dạng hình vuông có chu vi là 80 dm. Người ta phải dùng các viên gạch hình vuông để lát, mỗi viên gạch có độ dài cạnh 2 dm và có giá là 25 000 đồng/viên. Tính số viên gạch cần dùng và số tiền mua gạch để lát nền căn phòng đó.
 Xem đáp án
Xem đáp án
Độ dài cạnh của căn phòng là:
80 : 4 = 20 (dm)
Diện tích căn phòng là:
20 ´ 20 = 400 (dm2)
Diện tích 1 viên gạch là:
2 ´ 2 = 4 (dm2)
Để lát nền căn phòng cần số viên gạch là:
400 : 4 = 100 (viên)
Số tiền mua gạch để lát nền là:
25 000 ´ 100 = 2500 000 (đồng)
Đáp số: 2 500 000 đồng
Câu 42:
Một khu đất hình chữ nhật có diện tích 256 m2, chiều rộng là 8 m. Xung quanh khu đất người ta đóng cọc để rào xung quanh, biết rằng khoảng cách giữa hai cọc liền nhau là 4 m. Hỏi cần bao nhiêu cọc để đủ rào xung quanh khu đất đó.
 Xem đáp án
Xem đáp án
Chiều dài là: 256 : 8 = 32 (m)
Chu vi hình chữ nhật là: (8 + 32).2 = 80 (m)
Cần số cọc là: 80 : 4 = 20 (cọc)
Đáp số: 20 cọc.
Câu 43:
Phân số thập phân thích hợp điền vào chỗ chấm:
a) 0,7% = …
b) 50% = …
 Xem đáp án
Xem đáp án
a) \(0,7\% = \frac{{0,7}}{{100}} = \frac{7}{{1000}}\).
b) \(50\% = \frac{{50}}{{100}} = \frac{5}{{10}}\)
Câu 44:
Nếu gửi tiết kiệm theo kì hạn là 12 tháng thì lãi suất hàng tháng là 0,7%. Hỏi 1 người gửi 50 000 000 đồng trong 1 năm thì thu được bao nhiêu tiền lãi? (Tiền lãi của tháng không được cộng vào tiền gửi).
 Xem đáp án
Xem đáp án
Một năm thu được số tiền lãi là:
50 000 000 ´ 0,7% ´ 12 = 4 200 000 (đồng)
Đáp số: 4 200 000 đồng.
Câu 45:
Bạn Sơn tạo các hình bằng những chiếc tăm giống nhau theo sơ đồ nhứ hình trên (Hình thứ n có n2 ô vuông giống nhau và mỗi cạnh hình vuông là một chiếc tăm). Hỏi Sơn phải thêm bao nhiêu chiếc tăm vào hình thứ 2018 để được hình thứ 2019.
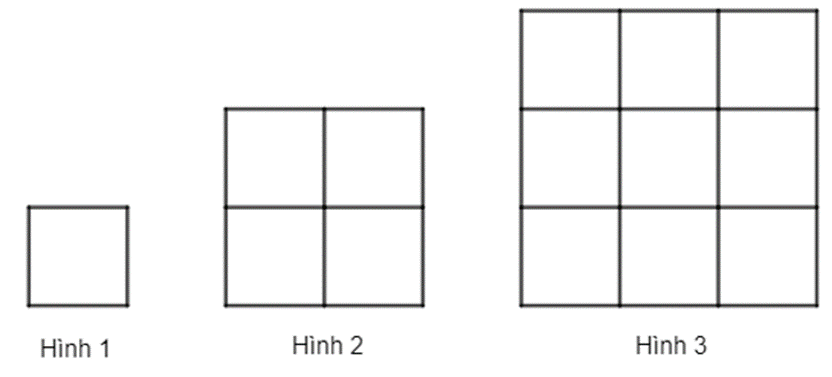
 Xem đáp án
Xem đáp án
• Với n = 1 ta có hình 12 = 1 ô vuông và cần dùng 4 = 2.1.(1 + 1) (chiếc tăm).
• Với n = 2 ta có hình 22 = 4 ô vuông và cần dùng 12 = 2.2.(2 + 1) (chiếc tăm).
• Với n = 3 ta có hình 32 = 9 ô vuông và cần dùng 24 = 2.3.(3 + 1) (chiếc tăm).
…
Như vậy mỗi số n ta có n2 và cần dùng 2n(n + 1) chiếc tăm để tạo thành.
• Với n = 2018 ta có: 20182 ô vuông và cần 2 . 2018 . 2019 (chiếc tăm).
• Với n = 2019 ta có: 20192 ô vuông và cần 2 . 2019 . 2020 (chiếc tăm).
Vậy từ hình thứ 2018 đến 2019 ta cần thêm số chiếc tăm là:
2 . 2019 . 2020 – 2 . 2018 . 2019 = 8 076 (chiếc tăm)
Đáp số: 8076 chiếc tăm
Câu 46:
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
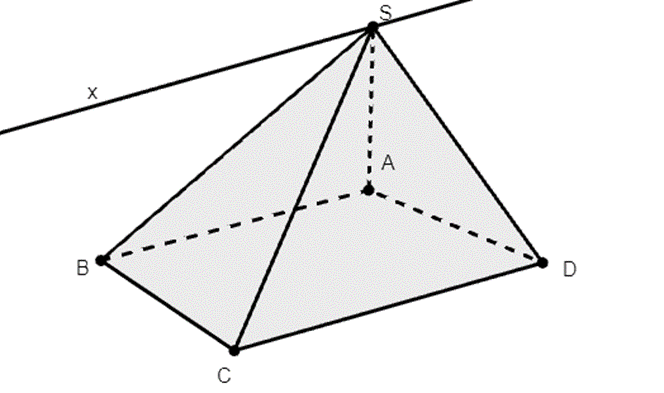
Vì AB//CD nên (SAB) cắt (SCD) theo giao tuyến là đường thẳng Sx, Sx//AB//CD.
Câu 47:
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của mp(SAD) và mp(SBC) là đường thẳng song song với đường thẳng nào trong số các đường thẳng sau?
 Xem đáp án
Xem đáp án
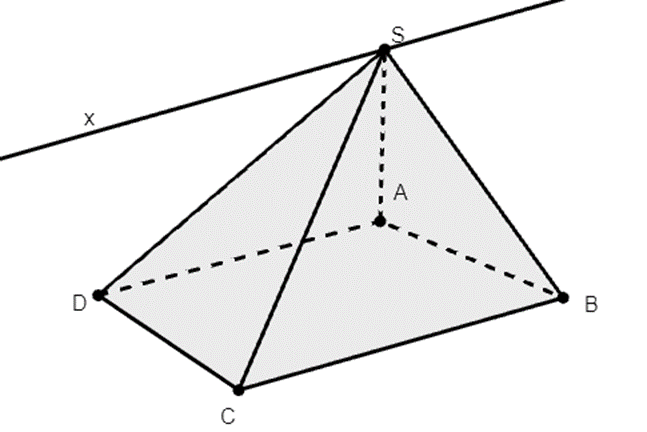
Xét (SAD) và (SBC) có:
S là điểm chung
AD // BC
Do đó giao tuyến của (SAD) và (SBC) là đường thẳng đi qua S và song song với AD.
Câu 48:
Tính đạo hàm của hàm số sau: \(y = \sqrt {x + \sqrt {{x^2} - x + 1} } \).
 Xem đáp án
Xem đáp án
Ta có: \(y' = {\left( {\sqrt {x + \sqrt {{x^2} - x + 1} } } \right)^\prime }\)
\( = \frac{1}{{2\sqrt {x + \sqrt {{x^2} - x + 1} } }}{\left( {x + \sqrt {{x^2} - x + 1} } \right)^\prime }\)
\( = \frac{1}{{2\sqrt {x + \sqrt {{x^2} - x + 1} } }}\left( {1 + \frac{{2x - 1}}{{2\sqrt {{x^2} - x + 1} }}} \right)\)
\( = \frac{{2\sqrt {{x^2} - x + 1} + 2x - 1}}{{4\sqrt {x + \sqrt {{x^2} - x + 1} .\sqrt {{x^2} - x + 1} } }}\).
Câu 49:
Tính đạo hàm số \(y = n\left( {x + \sqrt {{x^2} + 1} } \right)\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
\(y' = \frac{{{{\left( {x + \sqrt {{x^2} + 1} } \right)}^\prime }}}{{x + \sqrt {{x^2} + 1} }} = \frac{{1 + \frac{{{{\left( {{x^2} + 1} \right)}^\prime }}}{{2\sqrt {{x^2} + 1} }}}}{{x + \sqrt {{x^2} + 1} }}\)
\( = \frac{{1 + \frac{{2x}}{{2\sqrt {{x^2} + 1} }}}}{{x + \sqrt {{x^2} + 1} }} = \frac{{1 + \frac{x}{{\sqrt {{x^2} + 1} }}}}{{x + \sqrt {{x^2} + 1} }}\)
\( = \frac{{\sqrt {{x^2} + 1} + x}}{{\sqrt {{x^2} + 1} \left( {x + \sqrt {{x^2} + 1} } \right)}} = \frac{1}{{\sqrt {{x^2} + 1} }}\).
Câu 50:
Tìm điểm cố định mà đường thẳng y = (m – 2)x + 3 luôn đi qua với mọi giá trị của m.
 Xem đáp án
Xem đáp án
y = (m – 2)x + 3 (d)
Giả sử I(x0; y0) là điểm cố định mà (d) luôn đi qua.
Khi đó ta có:
y0 = (m – 2)x0 + 3
⇔ y0 = mx0 – 2x0 + 3
⇔ mx0 = y0 + 2x0 – 3
⇔ \(\left\{ \begin{array}{l}{x_0} = 0\\2{x_0} + {y_0} - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 0\\{y_0} = 3\end{array} \right.\)
Câu 51:
Cho hàm số y = (2m – 3)x + m – 1. Chứng minh rằng đồ thị hàm số đi qua điểm cố định với mọi giá trị của m. Tìm điểm cố định ấy.
 Xem đáp án
Xem đáp án
Gọi M(x0; y0) là điểm cố định mà đường thẳng (d) luôn đi qua. Khi đó ta có:
y0 = (2m – 3)x0 + m – 1
⇔ y0 = 2mx0 – 3x0 + m – 1
⇔ y0 – 2mx0 – 3x0 + m – 1 = 0
⇔ m(–2x0 + 1) + (y0 – 3x0 – 1) = 0
\[ \Rightarrow \left\{ \begin{array}{l} - 2{x_0} + 1 = 0\\{y_0} - 3{x_0} - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = \frac{1}{2}\\{y_0} = \frac{5}{2}\end{array} \right.\]
\( \Rightarrow M\left( {\frac{1}{2};\frac{5}{2}} \right)\)
Vậy với mọi m, họ các đường thẳng (d) có phương trình y = (m + 1)x + 2x – m luôn đi qua mọt điểm M cố định có tọa độ \(M\left( {\frac{1}{2};\frac{5}{2}} \right)\).Câu 52:
Tìm x, biết: \(\frac{{{8^x}}}{{{2^x}}} = 4\).
 Xem đáp án
Xem đáp án
\(\frac{{{8^x}}}{{{2^x}}} = 4\)
\({\left( {\frac{8}{2}} \right)^x} = 4\)
4x = 4
x = 1
Vậy x = 1.
Câu 53:
Viết kết quả phép tính dưới dạng một lũy thừa.
a) 32.93;
b) 22.52;
c) 85.23;
d) 98 : 32.
 Xem đáp án
Xem đáp án
a) 32 . 93 = 32 . (32)3 = 32 . 36 = 38;
b) 22.52 = (2.5)2 = 102;
c) 85 . 23 = (23)5 . 23 = 215 . 23 = 218;
d) 98 : 32 = (32)8 : 32 = 316 : 32 = 314.
Câu 54:
Cho △ABC nhọn các đường cao AD và BE cắt tại H. Gọi M là trung điểm BC. P đối xứng với H qua BC, Q đối xứng với H qua M.
a) PQ // BC. Tứ giác DMQP là hình gì?
b) Chứng minh rằng: HCQB là hình bình hành.
 Xem đáp án
Xem đáp án
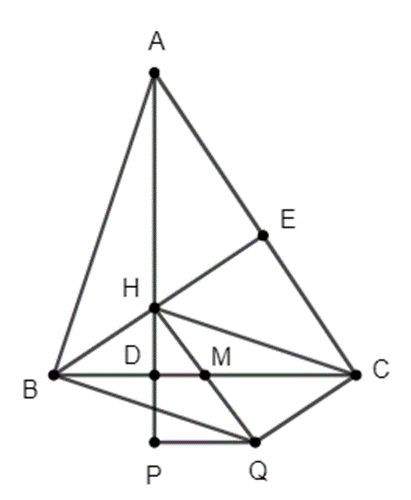
a) Vì H đối xứng với P qua BC nên BC là đường trung trực của HP, hay HP⊥BC tại trung điểm của HP.
Suy ra D là trung điểm của HP nên \(\frac{{HD}}{{PQ}} = 1\) (1)
Mặt khác: H đối xứng với Q qua M nên M là trung điểm của HQ nên \(\frac{{HM}}{{MQ}} = 1\) (2)
Từ (1) và (2) suy ra \(\frac{{HD}}{{DP}} = \frac{{HM}}{{MQ}}\)
Theo định lý Talet đảo thì DM // PQ hay BC // PQ (đpcm)
Tứ giác DMQP có DM // PQ và \(\widehat D = 90^\circ \) do HP⊥BC tại D
Do đó tứ giác DMQP là hình thang vuông.
b) Tứ giác HCQB có hai đường chéo BC, HQ cắt nhau tại trung điểm M của mỗi đường nên suy ra HCQB là hình bình hành (đpcm).
Câu 55:
Chứng minh rằng \(\frac{{3n + 4}}{{2n + 3}}\) là phân số tối giản.
 Xem đáp án
Xem đáp án
Gọi ƯCLN(3n + 4; 2n + 3) = d
Ta có: 3n + 4 ⋮ d.
2n + 3 ⋮ d
⇒ (2n + 3) – (3n + 4) ⋮ d
⇒ 3(2n + 3) – 2(3n + 4) ⋮ d
⇒ 6n + 9 – 6n – 8 ⋮ d
⇒ 1 ⋮ d
⇒ d = ± 1
Vì ƯCLN(3n + 4; 2n + 3) = 1 nên \[\frac{{3n + 4}}{{2n + 3}}\] là phân số tối giản.
Câu 56:
Chứng minh rằng với mọi số nguyên n thì phân số \(\frac{{{n^3} + 2n}}{{{n^4} + 3{n^2} + 1}}\) là phân số tối giản.
 Xem đáp án
Xem đáp án
Gọi d = ƯCLN (n3 + 2n, n4 + 3n2 + 1)
Ta có: n3 + 2n ⋮ d
⇒ n(n3 + 2n) ⋮ d
⇔ n4 + 2n2 ⋮ d (1)
(n4 + 3n2 + 1) – (n4 + 2n2) ⋮ d
⇒ n2 + 1 ⋮ d
⇒ (n2 + 1)2 = n4 + 2n2 + 1 ⋮ d (2)
Từ (1) và (2) suy ra:
(n4 + 2n2 + 1) – (n4 + 2n2) ⋮ d
⇒ 1 ⋮ d ⇒ d = ± 1
Vậy \(\frac{{{n^3} + 2n}}{{{n^4} + 3{n^2} + 1}}\) là phân số tối giản.
Câu 57:
Cho hàm số y = mx3 – mx2 – (m +4)x + 2. Xác định m để hàm số đã cho nghịch biến trên ℝ.
 Xem đáp án
Xem đáp án
Ta xét trường hợp hàm số suy biến. Khi m = 0, hàm số trở thành y = −x + 2. Đây là hàm bậc nhất nghịch biến trên ℝ. Vậy m = 0 thỏa mãn yêu cầu bài toán.
Với m ≠ 0, hàm số là hàm đa thức bậc 3.
Y’ = 3mx2 – 2mx2 – (m + 4)
Do đó hàm số nghịch biến trên ℝ khi và chỉ khi:
\(\left\{ \begin{array}{l}m < 0\\\Delta ' \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\{m^2} + 3m\left( {m + 4} \right) \le 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m < 0\\4{m^2} + 12m \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\ - 3 \le m \le 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m < 0\\ - 3 \le m \le 0\end{array} \right.\) ⇔ −3 ≤ m < 0.
Kết hợp 2 trường hợp ta được −3 ≤ m ≤ 0 0 thỏa mãn yêu cầu bài toán.
Câu 58:
Cho hàm số y = x3 – (m + 1)x2 – (m2 – 2m)x + 2020. Tìm m để hàm số nghịch biến trên khoảng (0; 1).
 Xem đáp án
Xem đáp án
Ta có:
Y’ = 3x2 – 2(m + 1)x – (m2 – 2m)
Khi đó y’ = 0
⇔ 3x2 – 2(m + 1)x – (m2 – 2m) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = m\\x = \frac{{m - 2}}{3}\end{array} \right.\)
Hàm số đã cho nghịch biến trên khoảng (0; 1) khi và chỉ khi:
\(\left[ \begin{array}{l}m \le 0 < 1 \le \frac{{m - 2}}{3}\\\frac{{m - 2}}{3} \le 0 < 1 \le m\end{array} \right. \Leftrightarrow 1 \le m \le \frac{3}{2}\)
Vậy với \(1 \le m \le \frac{3}{2}\) thỏa mãn yêu cầu bài toán.
Câu 59:
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn z(1 + i) là số thực là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C.
Giả sử ta có số phức z = x + yi. Ta có:
Z(1 + i) = (x + yi)(1 + i) = (x – y) + (x + y)i
Z(1 + i) là số thực khi x + y = 0 hay y = −x.
Câu 60:
Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \(z.\overline z = 1\) là
 Xem đáp án
Xem đáp án
Đặt z = a + bi \( \Rightarrow \overline z = a - bi\)
Ta có: \(z.\overline z = 1\)
⇔ (a + bi)(a – bi) = 1
⇔ a2 – b2i2 = 1
⇔ a2 + b2 = 1
Vậy tập hợp các số thực thỏa mãn điều kiện trên là một đường tròn có tâm là gốc tọa độ và có bán kính là 1 đvđt.
Câu 61:
Cho a là góc tù và \(\sin a = \frac{4}{5}\). Tính A = 2sina – cosa.
 Xem đáp án
Xem đáp án
Ta có: sin2a + cos2a = 1
⇒ cos2a = 1 – sin2a
⇒ cos2a = \(1 - {\left( {\frac{4}{5}} \right)^2}\)
\( = 1 - \frac{{16}}{{25}} = \frac{9}{{25}}\)
\( \Rightarrow \left[ \begin{array}{l}{\cos ^2}a = {\left( {\frac{3}{5}} \right)^2}\\{\cos ^2}a = {\left( {\frac{{ - 3}}{5}} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \cos a = \frac{{ \pm 3}}{5}\)
Mà a là góc tù nên cosa < 0
\( \Rightarrow \cos a = - \frac{3}{5}\)
\( \Rightarrow A = 2\sin a - \cos a = 2.\frac{4}{5} - \left( {\frac{{ - 3}}{5}} \right)\)
\( = \frac{8}{5} + \frac{3}{5} = \frac{{11}}{5}\)
Vậy \(A = \frac{{11}}{5}\).
Câu 62:
Cho hình chóp S.ABCD, đáy là hình bình hành tâm O. Gọi M, N, P, Q lần lượt là trung điểm SA, SB, SC và SD. Tìm giao tuyến của (MNPQ) và (SAC).
 Xem đáp án
Xem đáp án
Đáp án đúng là: D.
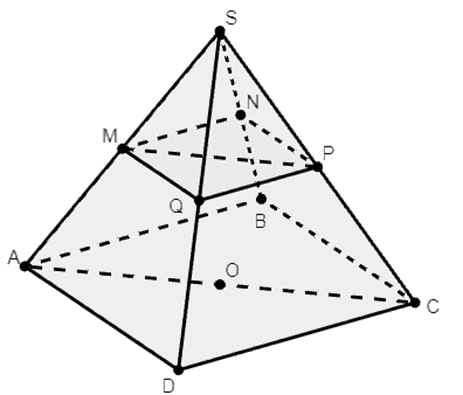
Ta có: M ∈ SA ⇒ M ∈ (SAC)
M ∈ (MNPQ)
⇒ M ∈ (SAC) ∩ (MNPQ) (1)
Mặt khác:
P ∈ (SC) ⇒ P ∈ (SAC)
P ∈ (MNPQ)
⇒ P ∈ (SAC) ∩ (MNPQ) (2)
Từ (1) và (2) suy ra (MNPQ) ∩ (SAC) = MP.
Câu 63:
Cho hình chóp S.ABCD là hình bình hành tâm O. M, N, P lần lượt là trung điểm của AD, SA, SB.
a) Tìm giao tuyến của (MNP) và (SAB).
b) Tìm giao tuyến của (MNP) và (SBD).
 Xem đáp án
Xem đáp án
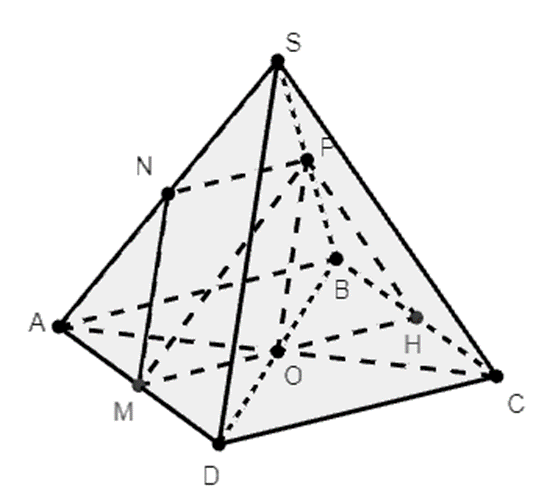
a) Xét tam giác SAB có NP là đường trung bình nên NP ∈ (SAB)
Mà NP ∈ (MNP).
Do đó NP là giao tuyến của (MNP) và (SAB).
b) Gọi H là trung điểm của BC
Suy ra MH là đường trung bình ở hình bình hành ABCD đi qua tâm O.
Mà (MNP) ⊂ (MNPH)
MH ∩ DB = {O}
Mà MH ∈ (MNPH) và DB ∈ (SDB)
Do đó (MNPH) ∩ (SDB) = O
Mặt khác ta có P ![]() SB ∈ (SDB)
SB ∈ (SDB)
Vậy PO là giao tuyến của (MNP) và (SBD).
Câu 64:
Xác định hàm số bậc hai y = ax2 + bx + c biết đồ thị của nó có đỉnh I(1; −1) và đi qua điểm A(2; 0)
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có đỉnh I(1; −1) ⇒ \( - \frac{b}{{2a}} = 1\) (1)
a + b + c = −1 (2)
Đồ thị hàm số đi qua A(2 ; 0)
⇒ 4a + 2a + c = 0 (3)
Từ (1); (2) và (3) ta có: a = 1; b = −2; c = 0.
Vậy hàm số cần tìm là: y = x2 – 2x.
Câu 65:
Xác định hàm số bậc hai y = 2x2 + bx + c biết đồ thị của nó có đỉnh I(−1; −2).
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì hàm số cần tìm có đỉnh là I(−1; −2) nên \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = - 1\\2 - b + c = - 2\end{array} \right.\)
Mà a = 2 nên \(\left\{ \begin{array}{l}b = 4\\c = 0\end{array} \right.\)
Vậy hàm số cần tìm là: 2x2 + 4x.
Câu 66:
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác vẽ các hình vuông ABDE, ACFG và BCHI. Ta có:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
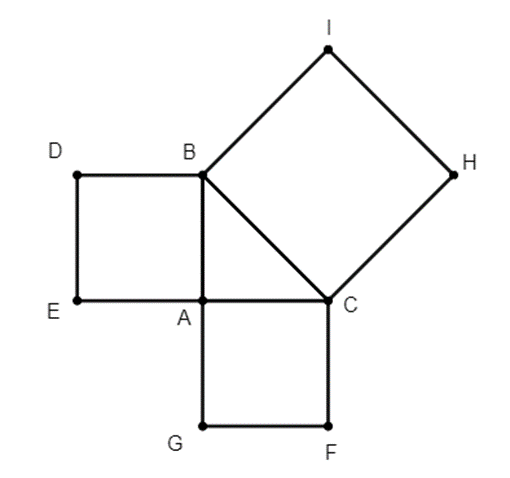
Ta có: SBCHI = BC2; SACFG = AC2; SABDE = AB2.
Theo định lý Py-ta-go cho tam giác ABC vuông tại A ta có: BC2 = AB2 + AC2
⇒ SBCHI = SACFG + SABDE
